Практическая работа №1 «Расчет и конструирование железобетонной балки таврового сечения». Практическая работа 1 Расчет и конструирование железобетонной балки таврового сечения

• Название: Практическая работа 1 Расчет и конструирование железобетонной балки таврового сечения
• Анкор: Практическая работа №1 «Расчет и конструирование железобетонной балки таврового сечения
• Дата: 22.04.2022
• Размер: 146.09 Kb.
• Имя файла: 1.docx
• Тип: Практическая работа; #489723

Государственное автономное профессиональное образовательное учреждение

Саратовской области

«Саратовский архитектурно-строительный колледж»


Практическая работа №1
«Расчет и конструирование железобетонной балки таврового сечения»
Вариант № 6

Выполнил студент Принял преподаватель:
группы 31 кс Огольцова Е.Г. Катышова А.С.

Саратов 2021

1. 
   Исходные данные.
   

Требуется рассчитать и законструировать однопролетную, свободно лежащую на опорах железобетонную балку таврового сечения, размером b 200 мм, h 600 мм, b'_f 450 мм, h'_f 80 мм на пролет L_п= 6 м для междуэтажного перекрытия, загруженную нагрузками: постоянной и нормативной от плиты и пола g^н= 3,3 кН/м², временной нормативной р^н= 5,0 кН/м². Шаг балок а_б= 4,8 м, глубина опоры l_оп= 250 мм.

Балка изготавливается из тяжелого бетона класса по прочности на сжатие

В 30 и при изготовлении подвергается тепловой обработке при атмосферном давлении. Продольная рабочая арматура из стержней периодического профиля класса А- II, поперечная из стержней класса А-I.

Расчетные характеристики материалов:

1) для бетона класса В 30 расчетное сопротивление для предельных состояний I группы (с учетом коэффициента γ_b2=0,9) осевому сжатию:

R_b× γ_b2 = 17 ×0,9= 15,3 МПа= 1,53 кН/см²; осевому растяжению:

R_bt× γ_b2 = 1,2 ×0,9= 1,08 МПа= 0,108 кН/см²;

Модуль упругости Е_b = 29 ×10³ МПа.

2) для продольной рабочей арматуры класса А- II расчетное сопротивление для предельных состояний I группы:

R_S = 280 МПа = 28 кН/см²;

для поперечной арматуры класса А-I расчетное сопротивление

R_Sw = 175 МПа = 17,5 кН/см²;

Модуль упругости Е_s=2,1×10⁵ МПа.

1.2 Определение расчетных нагрузок и усилий.

Расчетная нагрузка подсчитывается с грузовой площади:

А_гр=1× а_б=1×4,8 = 4,8 м².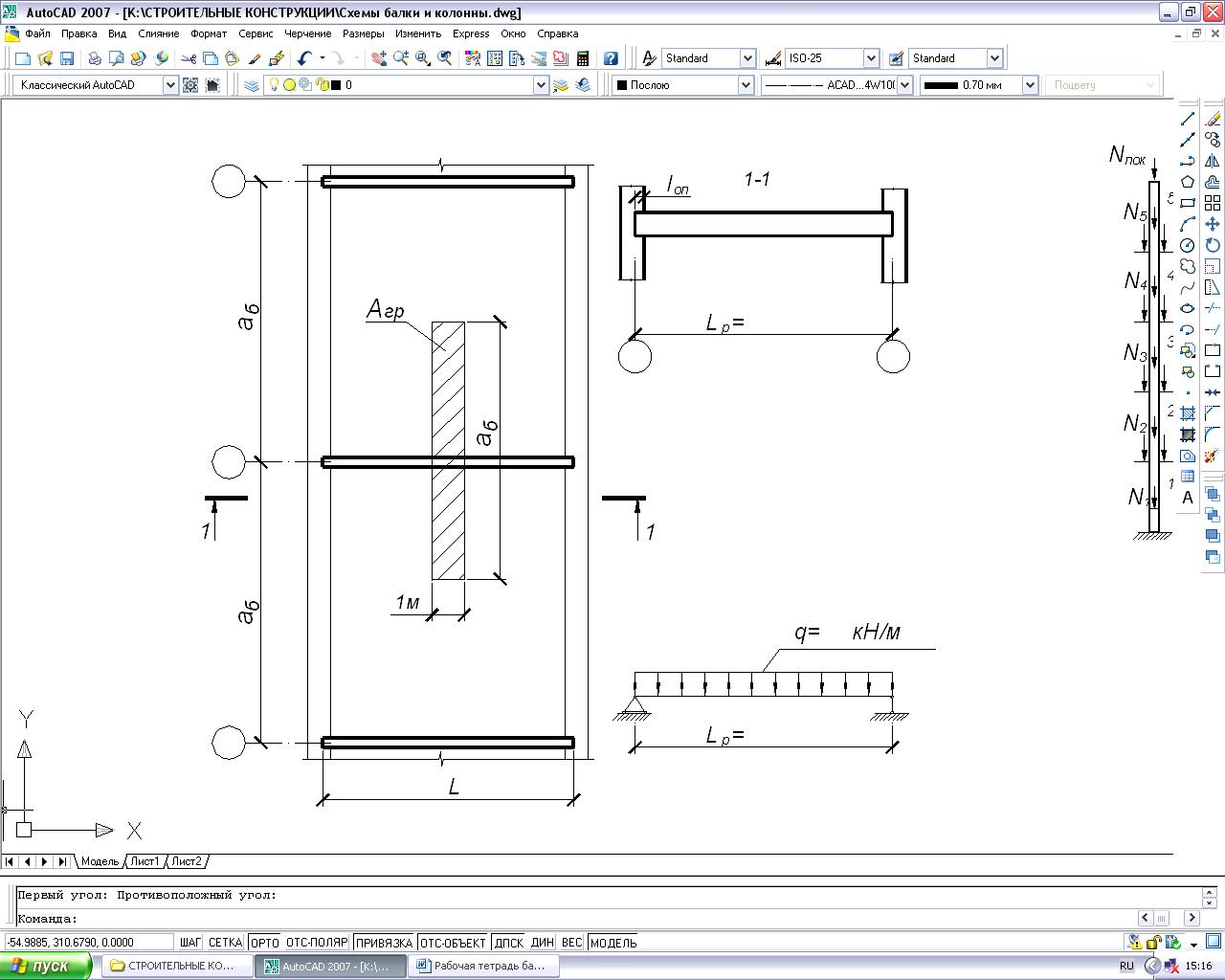



Рис.1 Схема загружения и расчетная схема балки
Расчетная нагрузка на 1 п.м. балки определяется по формуле:

q=(g^н×γ_fg + р^н×γ_fр)·А_гр, где

γ_fg =1,1 – коэффициент надежности по нагрузке для постоянной нагрузки (СНиП 2.01.07-85*); γ_fр =1,2 – то же для временной нагрузки.
q=( 3,3 ×1,1+ 5,0 ×1,2) 4,8 = 46,22 кН/м.

Расчетный изгибающий момент определяется по формуле: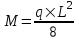





Расчетная поперечная сила определяется по формуле: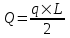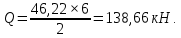

3. 
   Расчет прочности по сечению, нормальному к продольной оси
   

Принимаем расстояние от центра тяжести площади рабочей арматуры до нижней грани (защитный слой бетона) а=4см,

рабочая высота сечения h₀ = h - а = 60 - 4 = 56 см.

Определяем случай расчета таврового сечения по условию:

М≤М_x=hf´=R_b·γ_b2·b_f´·h_f´(h₀-0,5h_f´)
М_x=hf´= 1,7 × 0,9 × 45 × 8 ×( 56 -0,5×8 ) = 28642 кН·см.

М≥ Мx=hf´ имеем второй случай расчета. Сжатая зона находится в ребре.

Определяем момент, воспринимаемый свесами полки по формуле:

М_св= R_b·γ_b2·(b_f´-b)·h_f´(h₀-0,5_hf´)
М_св= 1,7 × 0,9 ×( 45 - 20 )× 8 ×( 56 - 0,5 × 8 ) = 15912 кН·см.
Соответствующее ему количество арматуры по формуле: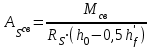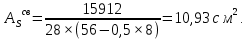




Определяем момент, воспринимаемый ребром по формуле:
М_р = М - М_св = 20799 - 15912 = 4887 кН·см.

Определяем коэффициент А₀ по формуле: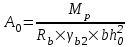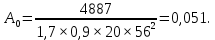





При А₀= 0,051 по таблице коэффициенты η= 0,975, ξ= 0,05.

Требуемая площадь сечения арматуры по формуле: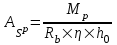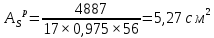





Суммарная площадь сечения арматуры А_s= +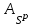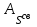

Аs= 5,27 + 10,93 = 16,2 см².

Армирование балки будет производиться двумя сварными каркасами, по сортаменту арматуры принимаем 3А- 28 с фактической площадью А_sf= 18,47 см².

1.4 Расчет прочности по сечению, наклонному к продольной оси.

Проверка необходимости расчета прочности наклонного сечения балки выполняется по условию:

Q≤k₁× R_bt×b×h₀,

где k₁=0,6 для тяжелого бетона.

Q= 138,66 кН >0,6× 0,108 ×20 × 56 =72,576 кН.

Условие не выполняется, поэтому необходим расчет прочности наклонного сечения.

В соответствии с требованиями норм принимаем при d= 28мм, диаметр поперечных стержней d_w= 8 мм.

Площадь этого стержня А_w= 0,503 см².

Количество поперечных стержней в сечении (2 каркаса) n=2, тогда их площадь

А_sw = n × А_w=2 × 0,503 = 1,006 см².

По конструктивным требованиям при h = 60 см на приопорных участках длиной L/4= 6/4= 1,5см, принимаем шаг поперечных стержней

S_w1=h/3= 60/3= 20 см,

на остальной части пролета S_w2=3/4 × h =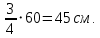

Рекомендуется шаг стержней S_w2=2× S_w1=2×20 = 40см.

Принимаем S_w2= 40 см.

Проверка прочности бетона по сжатой полосе между наклонными трещинами по формуле:

Q≤ 0,3 ×φ _w1 × φ _b1 × R_b × γ_b2 × b × h₀, где

φ_w1=1+5×α×μ_w – коэффициент, учитывающий влияние поперечной арматуры.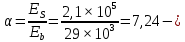

отношение модулей упругости.

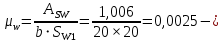коэффициент поперечного армирования.

φ_w1=1+5×μ_w×α=1+5× 0,0025 ·7,24=1,09 <1,3.

φ_b1 =1-β·R_b – коэффициент, учитывающий вид бетона.

Для тяжелого бетона β=0,01.

φ_b1 =1- 00,1 ·17 = 0,83.
Q= 138,66 кН < 0,3×1,09 ×0,83× 1,53 × 20×56 =465, 088 кН.

Условие выполняется, значит, размеры поперечного сечения балки достаточны.

Проверка прочности наклонного сечения при отсутствии отогнутой арматуры выполняется по условию:

Q≤ Q_b+Q_sw

Предварительно определяем:

- усилие в поперечных стержнях на 1 см длины балки по формуле: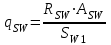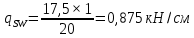





- длину проекции наиболее опасного наклонного сечения по формул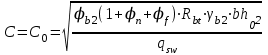е:

, где

φ_b2=2 – для тяжелого бетона;

φ_n=0 – при отсутствии продольной силы;

φ_f= 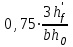- для балок таврового сечения с полкой в сжатой зоне.

φ_f=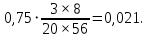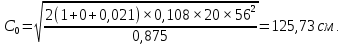



Что больше С_max=2·h₀= 2·56 = 112 см. Принимаем С= 112 см.

Поперечная сила, воспринимаемая бетоном по формуле: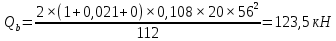





Поперечная сила, воспринимаемая поперечными стержнями по формуле:

Q_sw=q_sw×C
Q_sw= 0,875 × 112 = 98 кН.

Несущая способность наклонного сечения:
Q_b+Q_sw= 123,5 + 98 = 221,5 кН.
что больше Q = 138,66 кН.

Вывод: Прочность балки по наклонному сечению обеспечена.