Сопромат 2 вариант. Задание 2. споромат (Даша Иванова). Задание Рис. 1 Расчетная схема балки Определение опорных реакций

• Название: Задание Рис. 1 Расчетная схема балки Определение опорных реакций
• Анкор: Сопромат 2 вариант
• Дата: 10.09.2022
• Размер: 63.81 Kb.
• Имя файла: Задание 2. споромат (Даша Иванова).docx
• Тип: Документы; #669867

Задание 2.



Рис.1 — Расчетная схема балки
Определение опорных реакций

1) Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.





Найдем сумму моментов относительно шарнирно-подвижной опоры в точке A:



Найдем сумму моментов относительно шарнирно-неподвижной опоры в точке B:



2) Вычислим реакцию шарнирно-неподвижной опоры в точке B:



Так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону.

3) Вычислим реакцию шарнирно-подвижной опоры в точке A:



Так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону.

4) Решаем полученную систему уравнений, находим неизвестные: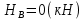



5) Выполним проверку решения, подставляя найденные значения в уравнение равновесия относительно оси Oy:



Построение эпюр

1) Рассмотрим первый участок 0 ≤ x₁ < 0.4

Продольная сила N:



Значения N на краях участка:





Поперечная сила Q:



Значения Q на краях участка: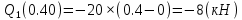





Изгибающий момент M:



Значения M на краях участка:





2) Рассмотрим второй участок 0.4 ≤ x₂ < 0.8

Продольная сила N:



Значения N на краях участка: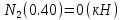





Поперечная сила Q: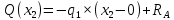



Значения Q на краях участка:





На этом участке эпюра Q пересекает горизонтальную ось. Точка пересечения: x = 0.27.

Изгибающий момент M:



Значения M на краях участка:





Локальный экстремум в точке x = 0.27:



3) Рассмотрим третий участок 0.8 ≤ x₃ < 1.6

Продольная сила N:



Значения N на краях участка:





Поперечная сила Q:



Значения Q на краях участка:





Изгибающий момент M:



Значения M на краях участка:





4) Рассмотрим четвертый участок 1.6 ≤ x₄ < 2

Продольная сила N:



Значения N на краях участка:





Поперечная сила Q:



Значения Q на краях участка: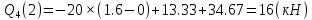





Изгибающий момент M:



Значения M на краях участка: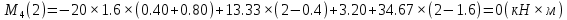





Подбор сечения

Из эпюры изгибающих моментов М определяем, что M_max = 6.4 (кН × м). Выполним перевод единиц измерения максимального изгибающего момента в с систему СИ: M_max = 6.4 (кН × м) = 6400 (Н × м).

Из эпюры поперечных сил Q определяем, что Q_max = 18.67 (кН). Выполним перевод единиц измерения максимальной поперечной силы в с систему СИ: Q_max = 18.67 (кН) = 18670 (Н).

Условие прочности при изгибе по нормальным напряжениям:



где: М_max - наибольший изгибающий момент;

W_x - момент сопротивления сечения относительно нейтральной оси Ox;

Заметим, что наибольшие нормальные напряжения в поперечных сечениях балки возникают в наиболее удаленных точках от нейтральной оси Oх, которая проходит через центр тяжести сечения.

Из условия прочности по нормальным напряжениям вычислим значение минимального требуемого момента сопротивления сечения:



Из сортамента выбираем ближайший больший номер сечения у которого:



Из сборника СТО АСЧМ 20-93 (Прокат стальной сортовой фасонного профиля. Двутавры горячекатаные с параллельными гранями полок. Технические условия) выбираем: Двутавр 14Б2

Геометрические характеристики выбранного сечения:

Момент сопротивления относительно оси Ox: W_x = 77.32 (см³)

Высота сечения: h = 14 (см)

Ширина сечения: b = 7.3 (см)

Толщина стенки: t_s = 0.47 (см)

Средняя толщина полки: t_f = 0.69 (см)

Статический момент полусечения относительно оси Ox: S_x = 44.17 (см³)

Осевой момент инерции относительно оси Ox: I_x = 541.22 (см⁴)
1) Проверим прочность выбранного сечения (Двутавр 14Б2) по нормальным напряжениям:



2) Определим, удовлетворяет ли принятое сечение балки (Двутавр 14Б2) условию прочности по касательным напряжениям:



где: - наибольшая поперечная сила;

- статическии момент отсеченной части поперечного сечения относительно нейтральной оси Oх;

- ширина поперечного сечения балки на уровне рассматриваемой точки;

- момент инерции всего сечения относительно нейтральной оси Ox;



Условия проверок выполняются. Сечение подобрано правильно. Окончательно из СТО АСЧМ 20-93 (Прокат стальной сортовой фасонного профиля. Двутавры горячекатаные с параллельными гранями полок. Технические условия) выбираем: Двутавр 14Б2

Размеры выбранного сечения:

Момент сопротивления относительно оси Ox: W_x = 77.32 (см³)

Высота сечения: h = 14 (см)

Ширина сечения: b = 7.3 (см)

Толщина стенки: t_s = 0.47 (см)

Средняя толщина полки: t_f = 0.69 (см)

Статический момент полусечения относительно оси Ox: S_x = 44.17 (см³)

Осевой момент инерции относительно оси Ox: I_x = 541.22 (см⁴)

Прямоугольное сечение балки подбираем из условия прочности при допустимом напряжении 100 (МПа):



где: - нормальные напряжения, МПа;

- наибольшее по абсолютной величине значение изгибающего момента, определяемое по эпюре Mx, кН × м;

– момент сопротивления, см³;

- допустимое значение нормального напряжения (расчетное сопротивление), МПа;

Момент сопротивления прямоугольного сечения определим по формуле:



Из эпюры изгибающих моментов М определяем, что M_max = 6.4 (кН × м)

Выполним перевод единиц измерения максимального изгибающего момента в с систему СИ: M_max = 6.4 (кН × м) = 6400 (Н × м).

Требуемый момент сопротивления определяем по формуле:



Из формулы момента сопротивления прямоугольного сечения получим:

Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.

Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=10 (мм), b=3840 (мм).

Круглое сечение балки подбираем из условия прочности при допускаемом напряжении 100 (МПа):



где: - нормальные напряжения, МПа;

- наибольшее по абсолютной величине значение изгибающего момента, определяемое по эпюре Mx, кН × м;

– момент сопротивления, см³;

- допустимое значение нормального напряжения (расчетное сопротивление), МПа;

Момент сопротивления круглого сечения определим по формуле:



Из эпюры изгибающих моментов М определяем, что M_max = 6.4 (кН × м)

Выполним перевод единиц измерения максимального изгибающего момента в с систему СИ: M_max = 6.4 (кН × м) = 6400 (Н × м)

Требуемый момент сопротивления определяем по формуле:



Подставив в последнее выражение значение , найдем диаметр сечения:



Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.

Следовательно, за окончательные размеры круглого сечения балки принимаем диаметр: d = 90 (мм).