|
|
2_Практическая работа по ЭИ_Excel. Практическая работа 2. Финансовые функции в ms excel 2010. Определение текущей стоимости инвестиции
Практическая работа №2. Финансовые функции в MS Excel 2010. Определение текущей стоимости инвестиции.
Цель работы. Решение экономических задач определения текущей стоимости инвестиции в табличном процессоре MS Excel 2010.
Ход работы:
Изучить теоретическую часть.
Выполнить задание практической части.
Представить файл для проверки преподавателю.
Теоретическая часть
Для расчета приведенной (к текущему моменту) стоимости инвестиции (начального значения) вклада (займа) используется функция ПС:
= ПС (Ставка; Кпер; Плт; Бс; Тип),
где Ставка – процентная ставка за один период;
Кпер (Число периодов) – общее число периодов выплат инвестиции;
Плт (Выплата) – это выплата, производимая в каждый период и не меняющаяся за все время выплаты инвестиции;
Бс – будущая стоимость или баланс, который нужно достичь после последней выплаты, если аргумент Бс опущен, то он полагается равным 0;
Тип – это число 0 или 1, обозначающее, когда производится выплата (1 – в начале периода, 0 – в конце периода), если аргумент Тип опущен, то он полагается равным 0.
Функция ЧПС возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования (дисконтирование – это определение стоимости денежного потока путём приведения стоимости всех выплат к определённому моменту времени) и стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения):
= ЧПС (Ставка; Значение1; Значение1;…),
где Ставка – ставка дисконтирования на один период;
Значение1 – значение1; значение2;… от 1 до 254 выплат и поступлений, равностоящих друг от друга по времени и происходящих в конце каждого периода.
В некоторой степени функции ПС и ЧПС похожи. Сравнивая их, можно сделать следующие выводы:
1) в функции ПС периодические выплаты предполагаются одинаковыми, а в функции ЧПС они могут быть различными;
2) в функции ПС платежи и поступления происходят как в конце, так и в начале периода, а в функции ЧПС предполагается, что все выплаты производятся равномерно и всегда в конце периода.
Из последнего вывода следует, что если денежный взнос осуществляется в начале первого периода, то его значение следует исключить из аргументов функции ЧПС и добавить (вычесть, если это затраты) к результату функции ЧПС. Если же взнос приходится на конец первого периода, то его следует задать в виде отрицательного первого аргумента массива значений функции ЧПС.
Нельзя непосредственно оценивать эффективность нескольких инвестиционных проектов, имеющих разную продолжительность. Предполагая, что допускается реинвестирование (дополнительное вложение собственного или иностранного капитала в экономику в форме наращивания ранее вложенных инвестиций за счет полученных от них доходов или прибыли), необходимо свести полученные результаты чистой текущей стоимости по каждому из них к единому по продолжительности периоду.
Для расчета чистой приведенной стоимости для графика денежных потоков используется функция ЧИСТЗ:
= ЧИСТЗ (Ставка; Значения; Даты),
где Ставка – ставка дисконтирования, применяемая к денежным потокам;
Значения – ряд денежных потоков, соответствующий графику платежей, приведенному в аргументе Даты;
Даты – расписание дат платежей, соответствующее ряду денежных потоков.
Практическая часть
Задание 1. Какую сумму необходимо положить в банк, выплачивающий 13,7% годовых, чтобы через 3 года получить 250 тыс. руб.
Для этого выполните действия:
Запустите Excel. Сохраните файл под именем «Ваша фамилия2», например, Иванов2.
Переименуйте Лист1, дав ему имя Задание12.
Так как требуется найти текущее значения вклада в банк, то примените финансовую функцию ПС. Для расчета результата функции курсор устанавливите в ячейку A1.
Осуществите вызов Мастера функции. На первом шаге Мастера функций выполните выбор категории Финансовые. Выберите в списке финансовую функцию ПС. В диалоговое окно введите значения аргументов (рис. 2.1).
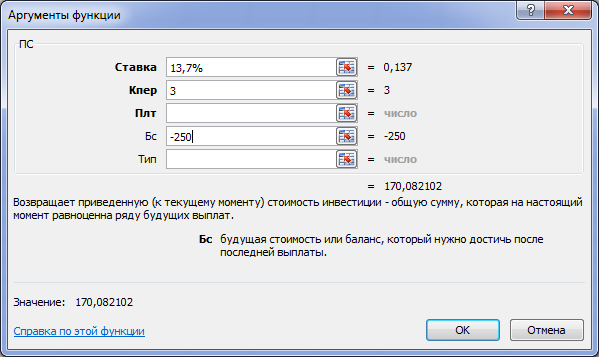
Рис. 2.1 Окно Аргументы функции ПС
Нажмите кнопку ОК для запуска расчета значения встроенной функции ПС. Таким образом, в банк необходимо положить 170,08 тыс.руб.
Задание 2. Платежи в фонд будут вноситься ежегодно по 200 тыс. руб. в течении 4 лет с начислением на них сложных процентов по ставке 8% годовых. Определите современную сумму всех платежей с начисленными процентами.
Для этого выполните действия:
Установите курсор в ячейку A2. Осуществите вызов Мастера функции. Выберите в списке финансовую функцию ПС.
В диалоговое окно введите значения аргументов (рис. 2.2). По условию Плт = -200 (означающее вложение денег). Аргумент Тип = 0 означает аннуитет постнумерандо (взносы в конце года).
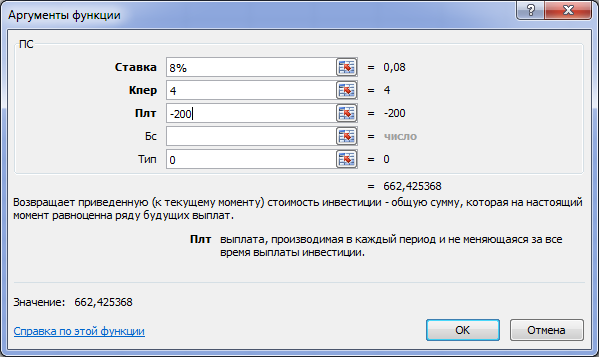
Рис. 2.2 Окно Аргументы функции ПС
Нажмите кнопку ОК для запуска расчета значения встроенной функции ПС. Величина фонда составляет 662,43 тыс. руб., его величина на настоящий момент равноценна ряду будущих выплат.
Задание 3. Инвестиции в проект составляют 800 тыс.руб. Ожидаются следующие доходы по проекту: 250 тыс.руб., 320 тыс.руб., 210 тыс.руб., 400 тыс.руб., 150 тыс.руб. заданы конкретные даты: выплата – 01.01.2015 г., поступления – 02.02.2015 г., 15.03.2015 г., 25.03.2015 г., 10.04.2015 г., 20.04.2015 г. соответственно. Издержки привлечения капитала 7%. Расчитать чистую текущую стоимость проекта.
Для этого выполните действия:
Перейдите на Лист2, дав ему имя Задание3.
Составьте таблицу, представленну на рис. 2.3. Обратите внимание, что значение начальной выплаты должно быть введено со знаком минус.
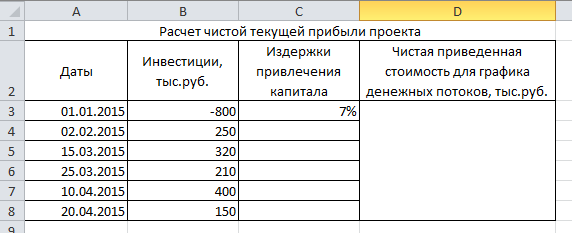
Рис. 2.3 Расчет чистой текущей прибыли проекта
Так как требуется найти чистую текущую стоимость проекта для графика денежных потоков, то примените финансовую функцию ЧИСТНЗ. Для расчета результата функции курсор устанавливите в ячейку D3.
Осуществите вызов финансовой функции ЧИСТНЗ. В диалоговое окно для ввода аргументов введите ссылки на адреса ячеек (рис. 2.4).
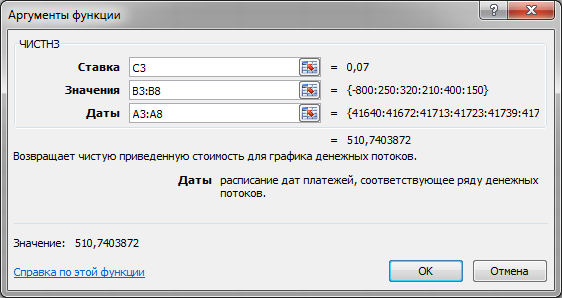
Рис. 2.4 Окно Аргументы функции ЧИСТНЗ
Нажмите кнопку ОК для запуска расчета значения встроенной функции ЧИСТНЗ. Чистая текущая стоимость проекта состаляет 510,74 тыс. руб.
Задание 4. Рассчитайте текущую стоимость вклада, который через 5 лет составит 150 тыс. руб. при ставке 9 % годовых. Постройте таблицу и диаграмму, отражающую динамику текущей стоимости вклада по годам.
Для этого выполните действия:
Перейдите на Лист3, дав ему имя Задание4.
Составьте таблицу, представленну на рис. 2.5. Так как проценты начисляются раз в год, то ставка и количество периодов остаются неизменными. Аргумент Бс = -150000, а Плт = 0.
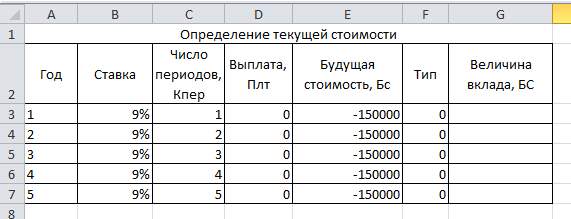
Рис. 2.5 Расчет текущей стоимости вклада (таблица)
Примените финансовую функцию ПС. Для расчета результата функции курсор устанавливите в ячейку G3.
Осуществите вызов финансовой функции ПС. В диалоговое окно для ввода аргументов введите ссылки на адреса ячеек (рис. 2.6).
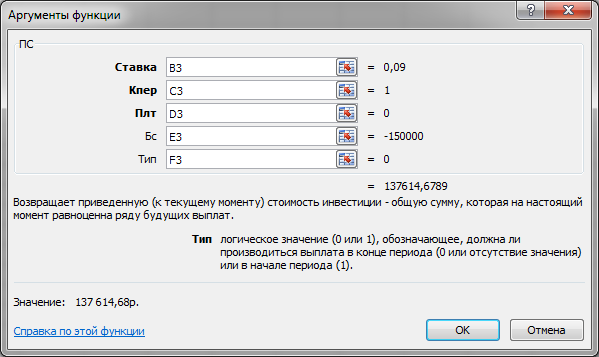
Рис. 2.6 Окно Аргументы функции ПС
Нажмите кнопку ОК для запуска расчета значения встроенной функции ПС.
Скопируйте формулу из G3 в ячейки G4:G7. Результаты расчетов, показывают, что для того чтобы на счете клиента банка было 150 тыс.руб. через 1 год при ставке 9 % годовых вклад должен составлять 137 614,68 руб. Для накопления той же суммы через 2 года первоначальный вклад должен быть равным 126 252,00 руб. и т.д.
Постройте гистограмму по диапазону ячеек G3:G7, отражающую динамику текущей стоимости вклада по годам (рис. 2.7).
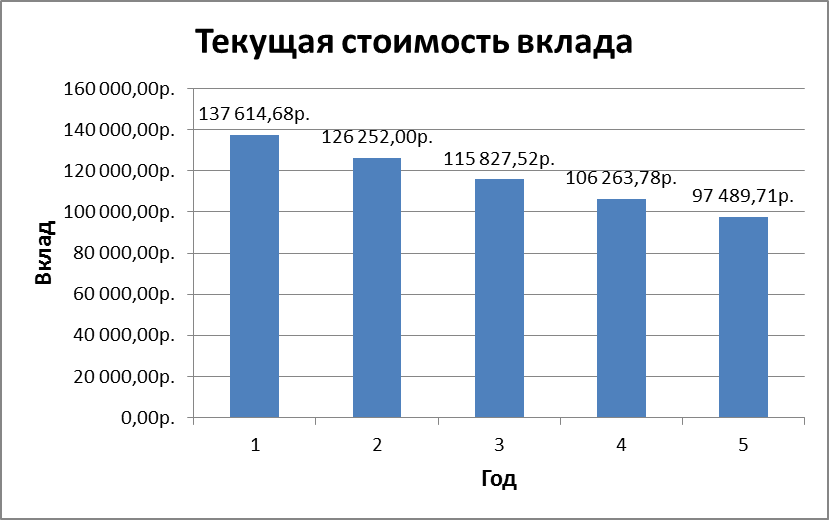
Рис. 2.7 Динамика текущей стоимости вклада по годам
Задание 5. Инвестор с целью инвестирования рассматривает 2 проекта, рассчитанных на 5 лет. Проекты характеризуются следующими данными:
по 1-му проекту начальные инвестиции составляют 550 тыс. руб., ожидаемые доходы за 5 лет соответственно 100, 190, 270, 300 и 350 тыс. руб.;
по 2-му проекту начальные инвестиции составляют 650 тыс. руб., ожидаемые доходы за 5 лет соответственно 150, 230, 470, 180 и 320 тыс. руб.
Определить, какой проект является наиболее привлекательным для инвестора при ставке банковского процента – 15% годовых.
Для этого выполните действия:
Создайте Лист4, дав ему имя Задание5.
Составьте таблицу, представленну на рис. 2.8.
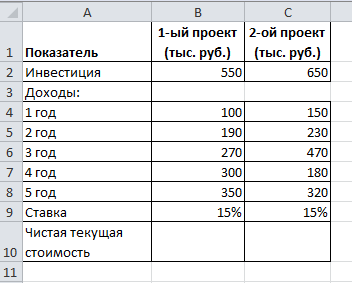
Рис. 2.8 Исходные данные (задание 5)
Примените финансовую функцию ЧПС. Для расчета результата функции курсор устанавливите в ячейку B10.
Осуществите вызов финансовой функции ЧПС. В диалоговое окно для ввода аргументов введите ссылки на адреса ячеек (рис. 2.9).
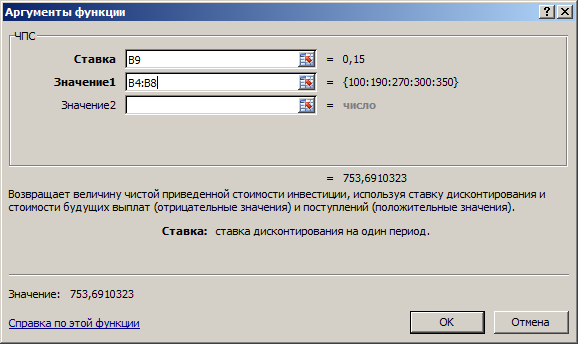
Рис. 2.9 Окно Аргументы функции ЧПС
Нажмите кнопку ОК для запуска расчета значения встроенной функции ЧПС. Скопируйте формулу из B10 в ячейкe C10.
Поскольку оба проекта предусматривают начальные инвестиции, отнимите их из результата, полученного с помощью функции ЧПС (начальные инвестиции по проекту не нужно дисконтировать, так как они являются предварительными, уже совершенными к настоящему моменту времени). Таким образов в ячейке B10 будет содержаться формула =ЧПС(B9;B4:B8)-B2, а в ячейке C10 формула =ЧПС(C9;C4:C8)-C2.
Результаты расчетов, показывают, что второй проект является для инвестора более привлекательным, так как чистая приведенная стоимость инвестиций во второй проект почти на 22 тыс. руб. выше, чем в первый.
Сохраните файл и закройте MS Excel. Представьте файл для проверки преподавателю.
Контрольные задания
Выполните расчеты с использованием финансовых функций. Оформите решение в виде таблицы и постройте диаграмму, отражающую динамику текущей стоимости вклада по годам (тип диаграммы выберите самостоятельно). Если в задаче не указано, в конце или в начале расчетного периода производится выплата, считать, что выплата производится в конце периода (аргумент Тип = 0).
Рассчитайте текущую стоимость вклада, который через три года составит 15000 тыс. руб. при начислении 20 % в год.
Определите текущую стоимость платежей в начале каждого месяца размером 100 тыс. руб. в течение 5 лет, если процентная ставка составляет 12 % годовых.
Определите текущую стоимость ежемесячных платежей размером 50 тыс. руб. в течение двух лет при начислении 18 % годовых.
Рассчитайте, какую сумму необходимо положить на депозит, чтобы через 4 года она достигла значения 20 млн. руб. при начислении 9 % годовых.
Определите текущую стоимость ежеквартальных платежей размером 350 тыс.руб. в течение 7 лет, если ставка процента – 11 % годовых.
Какую сумму необходимо положить на депозит под 16,5 % годовых, чтобы получить через три года 44 млн. руб. при полугодовом начислении процентов?
Определите текущую стоимость платежей размером 120 тыс. руб. в начале каждого месяца в течение четырех лет, если годовая процентная ставка — 14 %.
Рассчитайте текущую стоимость вклада, который через три года составит 15000 тыс. руб. при ставке процента 20% годовых.
Определите текущую стоимость ежемесячных платежей размером 100 тыс. руб. в течение пяти лет, если процентная ставка составляет 12 % годовых.
Определите текущую стоимость ежемесячных платежей размером 50 тыс. руб. в течение двух лет при ставке процента 18 % годовых.
Рассчитайте, какую сумму надо положить на депозит, чтобы через четыре года она выросла до 20000 руб. при норме процента 9 % годовых.
Определите текущую стоимость ежеквартальных платежей размером 350 тыс. руб. в течение семи лет, если ставка процента – 11% годовых.
Рассчитайте текущую стоимость вклада, который через пять лет составит 5000 тыс. руб. при начислении 10 % в год.
Определите текущую стоимость ежеквартальных платежей размером 250 руб. в течение 8 лет, если процентная ставка составляет 9,5 % годовых.
Определите текущую стоимость ежегодных платежей размером 20 тыс. руб. в течение трех лет при начислении 16 % годовых.
Рассчитайте, какую сумму необходимо положить на депозит, чтобы через 3 года она достигла значения 5 млн. руб. При начислении 8 % годовых.
Определите текущую стоимость ежемесячных платежей размером 150 тыс. руб. в течение 5 лет, если ставка процента – 10 % годовых.
Какую сумму необходимо положить на депозит под 9,5 % годовых, чтобы получить через четыре года 16 млн. руб. при ежеквартальном начислении процентов?
Определите текущую стоимость платежей размером 20 тыс. руб. в течение шести лет, если годовая процентная ставка – 14 %. Проценты вносятся каждые полгода.
Рассчитайте текущую стоимость вклада, который через семь лет составит 50 тыс. руб. при ставке процента 9 % годовых.
Рассчитайте, какую сумму необходимо положить на депозит, чтобы через 3 года она достигла значения 10 млн. руб. при начислении 4 % годовых.
Определите текущую стоимость полугодовых платежей размером 50 тыс. руб. в течение 5 лет, если ставка процента – 9 % годовых.
Какую сумму необходимо положить на депозит под 16 % годовых, чтобы получить через четыре года 25 млн. руб. при ежеквартальном начислении процентов?
Рассчитайте текущую стоимость вклада, который через три года составит 15000 тыс. руб. при начислении 20 % в год.
Определите текущую стоимость ежеквартальных платежей размером 350 тыс.руб. в течение 7 лет, если ставка процента – 11 % годовых.
|
|
|
 Скачать 305.5 Kb.
Скачать 305.5 Kb.








