Задача о транспортных расходах. Лаба 2. Практическая работа 2 По дисциплине Методы оптимизации Выполнил Проверил Курск
 Скачать 92.36 Kb. Скачать 92.36 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное образовательное учреждение высшего образования «Юго-Западный государственный университет» Практическая работа №2 По дисциплине «Методы оптимизации» Выполнил Проверил: Курск Задание: на предприятии X осуществляются транспортные перевозки с помощью четырех компаний до пяти населенных пунктов. Руководство компании решило распределить все количество перевозок между поставщиками транспортных услуг (транспортными компаниями) в определенной пропорции, выраженной в процентном соотношении — удельный вес в общем количестве перевозок. Известны также тарифы транспортных компаний за одну ездку и количество плановых перевозок до каждого населенного пункта в планируемом периоде. Пример 1 Необходимо оптимально распределить ездки в населенные пункты между транспортными компаниями таким образом, чтобы транспортные расходы были минимальными Ячейка Н13: =СУММ(D12:H12), Ячейка J8: =I8*$H$13. Данную формулу из ячейки J8 протаскиваем (копируем) в ячейки J9, J10, J11. Ячейка J12: =СУММ(J8:J11). Значения в ячейках D24:Н27 получены перемножением количества ездок (ячейки D19:Н22) на тарифы (ячейки D8:Н12). В ячейку D24 запишем формулу: =D19*D8. Протащим (скопируем) формулу в ячейки D25:D27 и E24:Н27. В ячейках D23:I23 формируются итоговые суммы транспортных услуг в разрезе пунктов назначения. Запишем в ячейку D23 формулу: =СУММ(D24:D27). Протащим (скопируем) эту формулу в ячейки Е23:I23. В ячейках I24:I27 формируются итоговые суммы транспортных услуг в разрезе компаний, оказывающих эти услуги. Запишем в ячейку I24 формулу: =СУММ(D24:H24). Протащим (скопируем) ее в ячейки I25:I27. 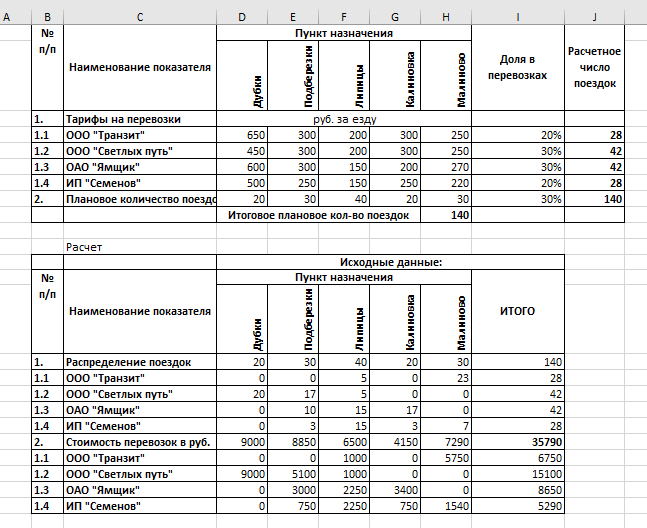 Расчет оптимальных перевозок Задача — подобрать в ячейках D19:Н22 такие значения, чтобы в ячейке I23 была рассчитана минимальная сумма расходов на транспорт. Для этого воспользуемся инструментом «Поиск решений». В строке «Оптимизировать целевую функцию» будет стоять адрес оптимизируемой ячейки, в данном случае — $I$23. Выберем цель, поставив флажок «Минимум». В строке «Изменяя ячейки переменных» помещаются адреса ячеек, которые необходимо будет подобрать для достижения желаемого результата ($D$19:$Н$22). В поле запишем ограничения в соответствии с ограничениями. Для этого воспользуемся кнопкой «Добавить», которая откроет окно «Добавить ограничения». Введем одно из ограничений: $D$19:$H$22 = целое, $D$12:$H$12 = $D$18:$H$18, $J$8:$J$11 = $I$19:$I22. 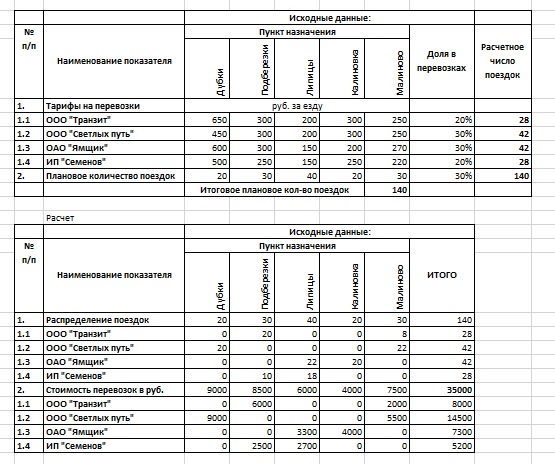 Результаты оптимизации Пример 2 В ячейках J8:J11 запишем формулу, позволяющую округлить вычисляемые значения до целого числа, которая имеет вид: Ячейка J8: =ОКРУГЛ(I8*$H$13;0). Протащим (скопируем) эту формулу в ячейки J9:J11. В ячейках D19:H22 распределим количество ездок для каждой транспортной компании до каждого пункта назначения, используя следующие ограничения: D19:H22 = целое, D12:H12 = D18:H18, J8:J11 = I19:I22. В ячейках D19:Н22 представлены данные, полученные в ходе оптимизации с помощью инструмента «Поиск решений». В результате минимизации в ячейке I23 получено значение 44 990 руб. 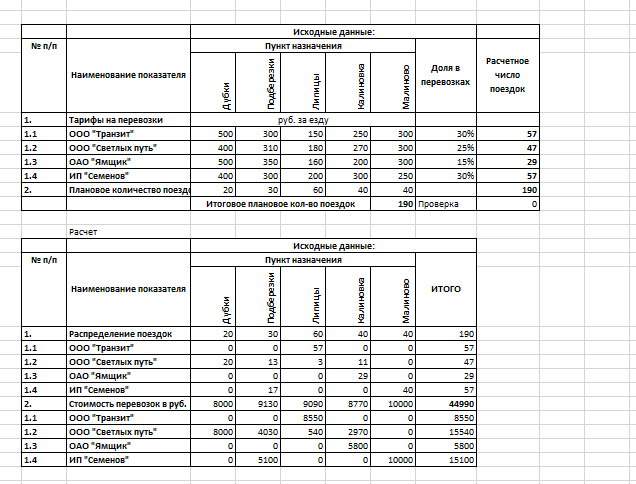 Результат оптимизации примера с округлением Вывод: таким образом, мы с помощью программы Excel смогли решить задачу оптимизации, связанную с осуществлением транспортных перевозок. Мы оптимально распределили ездки в населенные пункты между транспортными компаниями так, чтобы транспортные расходы оказались минимальными. |
