Практическая работа №2. Практическая работа 2 по дисциплине Основы гидравлики и термодинамики раздел Основы термодинамики
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Методические указания к практической работе 2.2 Теоретические положения расчета температурного поля бесконечной пластины при нестационарном процессе теплопроводности подробно изложены на с.66-78 учебника [1]. Для выполнения практической работы 2.2 удобно использовать известную теоретическую зависимость между относительной безразмерной температурой ( 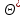 ) и критериями Фурье (Fo) и Био (Bi) для характерных точек пластины — поверхности и центра: ) и критериями Фурье (Fo) и Био (Bi) для характерных точек пластины — поверхности и центра: 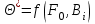 (2.1) (2.1)справедливой для тел так называемой простейшей или классической формы, к которым относят бесконечную (неограниченную) пластину, бесконечный (неограниченный) цилиндр и шар (сферу). В зависимости (2.1): 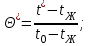 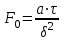 ; ; 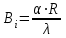 (2.2) (2.2)где 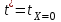 – температура середины пластины (теплового центра), К (оС), – температура середины пластины (теплового центра), К (оС), либо 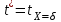 – температура поверхности пластины, К (оС); – температура поверхности пластины, К (оС); tж – температура окружающей среды, К (оС); 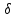 – половина толщины пластины, так как нагрев пластины происходит симметрично с обеих сторон, м; – половина толщины пластины, так как нагрев пластины происходит симметрично с обеих сторон, м; 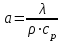 – коэффициент температуропроводности, м2/с; – коэффициент температуропроводности, м2/с; 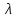 – коэффициент теплопроводности, Вт/(мК); – коэффициент теплопроводности, Вт/(мК); 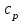 – удельная массовая теплоемкость, Дж/(кгК); – удельная массовая теплоемкость, Дж/(кгК); 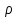 – плотность, кг/м3; – плотность, кг/м3; 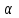 – коэффициент теплоотдачи, Вт/(м2К); – коэффициент теплоотдачи, Вт/(м2К); 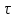 – время нагрева, с. – время нагрева, с.Зависимость (2.1) для бесконечной пластины изображена на графиках рисунок 2.1 и 2.2. 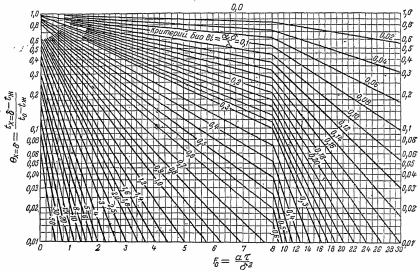 Рисунок 2.1 - Зависимость (2.1) для середины бесконечной пластины 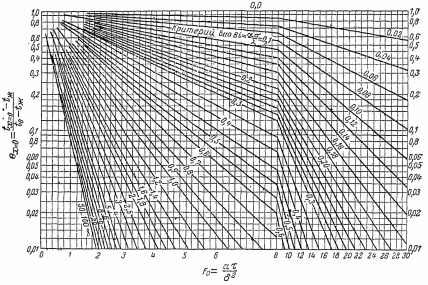 Рисунок 2.2 - Зависимость (2.1) для поверхности бесконечной пластины Если свойства и размеры пластины заданы, то в инженерных расчетах рассматривают две основные постановки задачи расчета нагрева (охлаждения) тел простейшей формы: прямую и обратную. При решении прямой задачи известны: — теплофизические свойства материала пластины: 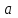 , , 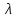 , , 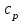 , , 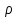 ; ; — толщина пластины: 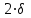 ; ; — коэффициент теплоотдачи: 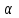 ; ; — начальная температура пластины: t0; — температура окружающей среды: tж; — время нагрева (охлаждения): 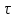 . .В результате решения прямой задачи находят температуру поверхности 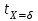 и температуру середины пластины (теплового центра) и температуру середины пластины (теплового центра) 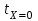 по следующему алгоритму: по следующему алгоритму: а) рассчитывают значения критериев Фурье и Био по формуле (2.2); б) по графикам на рисунках 2.1 и 2.2 находят значения относительной безразмерной температуры середины пластины 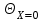 и ее поверхности и ее поверхности 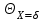 ; ;в) рассчитывают температуру в средней плоскости пластины и на ее поверхности по формуле 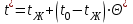 (2.3) (2.3)г) находят среднюю по массе температуру пластины tm при допущении параболического распределения температуры по ее сечению: 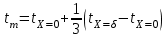 (2.4) (2.4)При решении обратной задачи определяют время ( 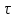 ), необходимое для достижения заданной температуры поверхности пластины ( ), необходимое для достижения заданной температуры поверхности пластины (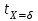 ) либо температуры ее средней плоскости ( ) либо температуры ее средней плоскости (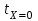 ). Также находят неизвестную по условию задачи температуру ( ). Также находят неизвестную по условию задачи температуру (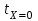 или или 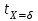 ) и среднемассовую температуру пластины. ) и среднемассовую температуру пластины.Для решения обратной задачи должны быть заданы: — теплофизические свойства материала пластины: 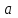 , , 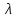 , , 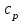 , , 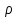 ; ; — толщина пластины: 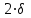 ; ; — коэффициент теплоотдачи: 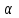 ; ; — начальная температура пластины: t0; — температура окружающей среды: tж; — температура либо поверхности пластины ( 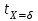 ), либо ее средней плоскости ( ), либо ее средней плоскости (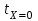 ) в конце нагрева. ) в конце нагрева.Алгоритм определения 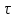 , , 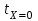 или или 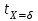 и tm заключается в следующем: и tm заключается в следующем: а) рассчитывают критерий Био и заданную относительную безразмерную температуру 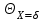 или или 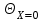 по формуле (2.2); по формуле (2.2); б) по графикам на рисунках 2.1 и 2.2 находят критерий Фурье, по значению которого рассчитывают время нагрева пластины: 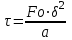 (2.5) (2.5)в) по найденному критерию Фурье и заданному критерию Био находят неизвестную относительную безразмерную температуру 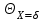 , если задана , если задана 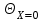 , и соответственно, находят , и соответственно, находят 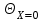 , если задана , если задана 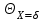 . Затем по формуле (2.3) рассчитывают температуру этой поверхности; . Затем по формуле (2.3) рассчитывают температуру этой поверхности; г) в заключение расчета по формуле (4) находят среднемассовую температуру пластины. Практическая работа 2.3 При заданных условиях конденсации определить: а) средний коэффициент теплоотдачи; б) тепловой поток, отводимый через стенку трубы при конденсации пара; в) расход конденсата, стекающего с трубы (режим конденсации рассматривать как пленочную конденсацию неподвижного пара). Данные, необходимые для выполнения практической работы 2.3, выбрать из табл. 2.4 согласно таблице вариантов Таблица 2.4 – Данные, необходимые для выполнения практической работы 2.3
Методические указания к практической работе 2.3 При пленочной конденсации сухого насыщенного пара на вертикальной трубе средний по высоте коэффициент теплотдачи определяется по формуле (3.1): а) ламинарный режим течения пленки конденсата (Z ⋜≼ 2300): 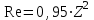 (3.1) (3.1)б) смешанный режим течения пленки конденсата — ламинарный режим на верхнем участке вертикальной трубы и турбулентный режим на нижнем участке: 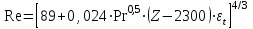 (3.2) (3.2)где 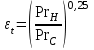 – поправочный коэффициент, учитывающий зависимость физических свойств пленки конденсата от температуры; критерии Прандтля – поправочный коэффициент, учитывающий зависимость физических свойств пленки конденсата от температуры; критерии Прандтля 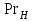 и и 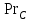 определяются для конденсата при температурах насыщения и средней температуре стенки. определяются для конденсата при температурах насыщения и средней температуре стенки.В вышеприведенных формулах: 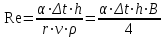 (3.3) (3.3)– критерий Рейнольдса при конденсации: 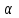 – коэффициент теплоотдачи, Вт/(м2К); – коэффициент теплоотдачи, Вт/(м2К); 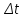 = tн – tc – температурный напор, оС; = tн – tc – температурный напор, оС; tн – температура насыщения, оС; tс – температура стенки трубы, оС; h – высота трубы, м; r – скрытая теплота парообразования, Дж/кг; 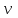 – кинематический коэффициент вязкости пленки конденсата, м2/с; – кинематический коэффициент вязкости пленки конденсата, м2/с; 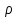 – плотность конденсата, кг/м3; – плотность конденсата, кг/м3; В = 4/(r 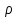 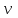 ) – комплекс, который находят по табл. 2.5. ) – комплекс, который находят по табл. 2.5.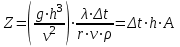 (3.4) (3.4)– приведенная высота трубы: g = 9,8 м/с2 – ускорение свободного падения;» – коэффициент теплопроводности конденсата, Вт/(мК); 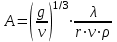 (3.5) (3.5)– комплекс, приведенный в табл. 2.5 в зависимости от температуры насыщения. Таблица 2.5 – Значения комплекса А и В в зависимости от температуры насыщения
Физические свойства конденсата находят по справочным таблицам, например, задачника [2] по температуре насыщения конденсата. Значение удельной теплоты фазового перехода (r) также находят по температуре насыщения или по заданному давлению сухого насыщенного пара по таблицам термодинамических свойств воды и водяного пара [12] или воспользоваться данными табл. 2.6 настоящих методических указаний. Таблица 2.6 – Зависимость температуры и теплоты парообразования от давления
Заметим, что в расчетные формулы теплотдачи при конденсации r следует подставлять в Дж/кг! Рассчитав критерий Рейнольдса по одной из формул Re = f(Z) легко можно найти и значение коэффициента теплоотдачи при конденсации: 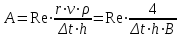 (3.6) (3.6)Алгоритм расчета теплоотдачи при конденсации на горизонтальной трубе незначительно отличается от изложенного выше. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
