|
|
надежность систем управления систем. Практическая работа 2. Практическая работа 2. Показатели надежности объекта Цель приобретение навыков расчета показателей надежности невосстанавливаемого объекта
Практическая работа №2.
Показатели надежности объекта
Цель: приобретение навыков расчета показателей надежности невосстанавливаемого объекта.
Задачи:
Основные теоретические сведения
Рассмотрим временной интервал работы t [0…τ]: [0…τ]:
при t=0 элемент начинает работать;
при t=τ происходит его отказ.
Время τ имеет случайный характер, поэтому в качестве основных функций, определяющих надежность элемента можно принять:
функцию распределения отказа
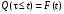 (1) (1)
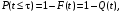 (2) (2)
Вероятность отказа
Вероятность отказа – это вероятность того, что в пределах заданной наработки или заданном интервале времени произойдет отказ объекта:
вероятностное определение (1):
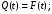 (3) (3)
статистическое определение:
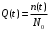 . (4) . (4)
где n(t) – число отказавших к моменту времени t изделий;
N0 – число изделий, поставленных на испытания.
Вероятность безотказной работы
Вероятность безотказной работы – это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает:
вероятностное определение (2):
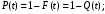 (5) (5)
статистическое определение:
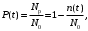 (6) (6)
где Nр –число работоспособных к моменту времени t изделий;
N0 – число изделий, поставленных на испытания.
Частота отказов (плотность распределения отказов)
вероятностное определение:
 (7) (7)
статистическое определение:
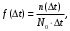 (8) (8)
где n(Δt) – число отказавших объектов в интервале Δt.
Интенсивность отказов
Интенсивность отказов – это условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не наступил:
вероятностное определение:
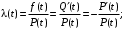 (9) (9)
статистическое определение:
 . (10) . (10)
гдеn(Δt) – число отказов однотипных объектов на интервале Δt, для которого определяется интенсивность отказов;
Nср – среднее число исправно работающих объектов в интервале Δt
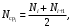 (11) (11)
Ni, Ni+1 –число исправно работающих объектов в начале и конце интервала Δt.
Общее выражение для вероятности безотказной работы
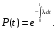 (12) (12)
Пояснение. Прологарифмируем формулу (10):
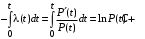 . .
Величина постоянной С определяется из условия, что t=0:
P(0)=1 и ln1=0; 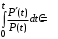 ; ; 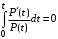 ; С=0. ; С=0.
Средняя наработка до отказа
Средняя наработка до отказа – математическое ожидание наработки объекта до первого отказа.
Вероятностное определение:
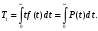
Статистическое определение
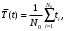 (13) (13)
где N0 – число работоспособных однотипных невосстанавливаемых объектов при t = 0 (в начале испытания);
ti – наработка до отказа i-го объекта.
Средняя наработка на отказ
 (14) (14)
где ti – наработка между i-1 и i-м отказами, ч;
n(t) – суммарное число отказов за время t.
Среднее время восстановления
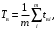 (15) (15)
m– число отказов последствия которых устранены;
tвi – время восстановления работоспособного состояния после i-го отказа.
Коэффициент готовности
Вероятность того, что изделие будет работоспособно в произвольный момент времени, кроме периодов, когда применение изделия по назначению исключено
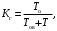 (16) (16)
где Tо− средняя наработка на отказ;
Tв− среднее время восстановления.
Коэффициент технического использования
Характеризует долю времени нахождения элемента в работоспособном состоянии относительно рассматриваемой продолжительности эксплуатации
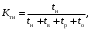 (17) (17)
где tн− суммарная наработка изделия в рассматриваемый промежуток времени;
tв, tpи tо− суммарное время, затраченное на восстановление, ремонт и ТО изделия за тот же период.
Примеры решения задач
Пример 1. На испытание поставлено N0=1000 однотипных электронных ламп. За 3000 ч отказало n(t)=80 ламп. Требуется определитьза период 3000 ч вероятность отказаQ(t) и вероятность безотказной работы P(t).
Решение
Вероятность отказа (4):
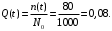
Вероятность безотказной работы (6)
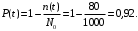
либо
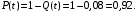
Пример 2. На испытание поставлено N0=1000 однотипных электронных ламп. За первые Δt1=3000 ч отказало 80 ламп, а за интервал времени Δt2=3000…4000 чотказало еще Δt2=50 ламп. Требуется определить частотуf(Δt2) и интенсивностьλ(Δt2) отказов электронных ламп в промежутке времени ∆t = 3000–4000 ч.
Решение
Частота отказов (7)
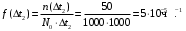
Интенсивность отказов (10)
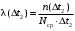 . .
Среднее число исправно работающих объектов в интервале (11)
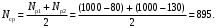
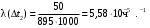
Пример 3. Три однотипных объекта поставлены на испытания. За период наблюдения было зафиксировано по первому объекту 6 отказов, по второму – 11, третьему – 8. Наработка первого объекта составила t1=181 ч, второго t2=329 ч, третьего t3=245 ч. Определить наработку объектов на отказ.
Решение
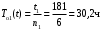 ��, ��, 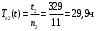 , , 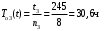
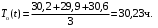
Пример 4. Пусть время работы элемента до отказа подчинено экспоненциальному закону λ=2,5·10–5 ч–1 (λ=const). Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку до отказа T при t=500, 1000, 2000 ч.
Решение
Выражение (12) при λ=cоnst примет вид
 . .
Тогда:
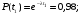 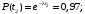 
Частота отказов (7):
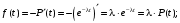
Тогда:
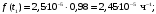 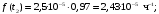
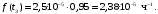
Т.к. средняя наработка на отказ – это математическое ожидание случайной наработки объекта до первого отказа, а математическое ожидание при экспоненциальном законе распределения
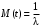 , ,
то
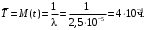
Пример 5. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn(t)=15 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1233 ч. Определить среднюю наработку на отказ To.
Решение
Наработка за указанный период составила
∆t=t1–t2=1233–258=975 ч.
Приняв 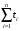 = 975 ч, определим среднюю наработку на отказ по статистическим данным (14) = 975 ч, определим среднюю наработку на отказ по статистическим данным (14)
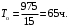
Пример 6. В аппаратуре было зафиксировано 8 отказов. Время восстановления составило: t1 = 12 мин, t2 = 23 мин, t3 = 15 мин, t4= 9 мин, t5= 17 мин, t6 = 28 мин, t7 = 25 мин, t8 = 31 мин.
Требуется определить среднее время восстановления аппаратуры tв.
Решение
Среднее время восстановления аппаратуры (2.14)
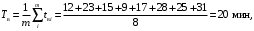
Пример 7. Аппаратура имела среднюю наработку на отказ То=65 ч и среднее время восстановления Тв=1,25 ч. Требуется определить коэффициент готовности Кг.
Решение
Коэффициент готовности (16)
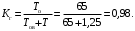
Пример 8. Известно, что интенсивность отказов λ= 0,02 ч–1, а среднее время восстановления tв=10 ч. Требуется вычислить коэффициент готовности и функцию готовности изделия. Закон распределения экспоненциальный.
Решение
Коэффициент готовности (16)
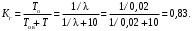
Пример 9. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Тэ=8760 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило tв=40 ч. Время проведения регламента составляет tо=20 ч. Суммарное время, затраченное на ремонтные работы за период эксплуатации составляет 15 суток (tр =15·24=360 ч).
Решение
Определим суммарное время наработки машины:
tн=Тэ – (tв+tр+tо)=8760 – (40+360+20)=8340.
Определим коэффициент технического использования (17)
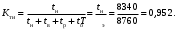
Пример 10. На испытание поставлено N0=400 изделий. За время t=3000 ч отказало n(3000)=200 изделий, за последующий интервал ∆t=100 ч отказало n(∆t)=100 изделий. Требуется определить вероятность безотказной работы P(t), частоту отказовf(t) и интенсивность отказовλ(t) за 3000, 3100, 3050 часов, частоту интенсивность λ(t) отказов в интервале 3000…3100 часов.
Решение
Вероятность безотказной работы (6):
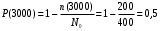 ; ;
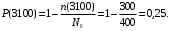
Среднее время исправно работающих изделий в интервале ∆t=100 ч:
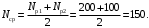
Число изделий, отказавших за время t=3050 ч:
n(3050)=N0–Nср=400–150=250.
тогда
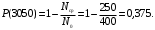
Частота отказа за 3000, 3100, 3050 часов (начало интервалов t=0):
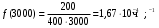
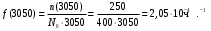
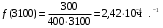
Интенсивность отказов за 3000, 3100, 3050 часов (начало интервалов t=0):
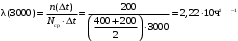 ; ;
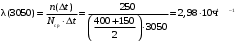 ; ;
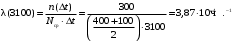
В интервале ∆t= 100 ч (начало интервала t=3000):
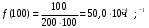
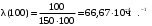
Задачи для решения
Задача 1. На испытание поставлено N0=1500 однотипных электронных ламп. За 5000 ч отказало n(t)=100 ламп. Требуется определитьза период 3000 ч вероятность безотказной работы P(t)и вероятность отказаQ(t).
Задача 2. На испытание поставлено N0=2000 однотипных приборов. За первые Δt1=3000 ч отказало 100 приборов, а за интервал времени Δt2=3000…4000 чотказало еще Δt2=100 приборов. Требуется определить частотуf(Δt2) и интенсивностьλ(Δt2) отказов приборов в промежутке времени ∆t = 3000–4000 ч.
Задача 3. Три однотипных объекта поставлены на испытания. За период наблюдения было зафиксировано по первому объекту 8 отказов, по второму – 10, третьему – 8. Наработка первого объекта составила t1=160 ч, второго t2=300 ч, третьего t3=240 ч. Определить наработку объектов на отказ.
Задача 4. Пусть время работы элемента до отказа подчинено экспоненциальному закону λ=2,5·10–5 ч–1. Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку до отказа 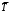 при t=1000, 2000, 3000 ч. при t=1000, 2000, 3000 ч.
Задача 5. В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрированоn(t)=10 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1000 ч. Определить среднюю наработку на отказ To
Задача 6. В аппаратуре было зафиксировано 10 отказов. Время восстановления составило: t1=10 мин, t2=20 мин, t3=12 мин, t4=10 мин, t5=15 мин, t6=25 мин, t7=25 мин, t8=30 мин.
Требуется определить среднее время восстановления аппаратуры tв.
Задача 7. Аппаратура имела среднюю наработку на отказ То=75 ч и среднее время восстановления tв=1,2 ч. Требуется определить коэффициент готовности Кг.
Задача 8. Известно, что интенсивность отказов λ= 0,01 ч–1, а среднее время восстановления tв=5 ч. Требуется вычислить коэффициент готовности. Закон распределения экспоненциальный.
Задача 9. Определить коэффициент технического использования машины, если известно, что машину эксплуатируют в течение года Тэ=9010 ч. За этот период эксплуатации машины суммарное время восстановления отказов составило tв=50 ч. Время проведения регламента составляет tо=10 ч. Суммарное времяtр, затраченное на ремонтные работы за период эксплуатации составляет 10 суток.
Задача 10. На испытание поставлено N0=500 изделий. За время t=3000 ч отказало n(3000)=100 изделий, за интервал ∆t=100 ч отказало n(∆t)=50 изделий. Требуется определить вероятность безотказной работы P(t), частоту отказовf(t) и интенсивность отказовλ(t) за 3000, 3100, 3050 часов, частоту интенсивность λ(t) отказов в интервале 3000…3100 часов. |
|
|
 Скачать 139.16 Kb.
Скачать 139.16 Kb.