Задача Определить наработку на отказ t 0 и коэффициент готовности к г
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
|
Занятие 4. Задача 1. Определить наработку на отказ T0 и коэффициент готовности Кг прибора после начала работы Т=500 ч, если интенсивность отказов составляет λ=60*10-6 1/ч, интенсивность восстановления после отказа µ=0.5 1/ч. Допустимое время обслуживания t=2 ч. Найти также ВБР для 500 часов. Решение. 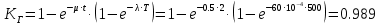 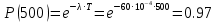 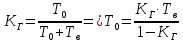 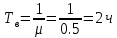 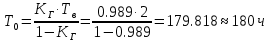 Задача 2. Определить надежность машины, состоящей из 5 последовательных блоков, для трёх интервалов работы: 1000, 3000, 5000 ч. Причем λ у всех разные: λ1=0.01*10-6 1/ч, λ2=0.05*10-6 1/ч, λ3=0.4*10-6 1/ч, λ4=3*10-6 1/ч, λ5=1*10-6 1/ч. Определить наработку на отказ Т0. Решение. λ постоянные, значит закон экспоненциальный. Напоминание. Предыдущие формулы. Вероятность безотказной работы (ВБР): 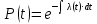 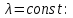 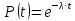 Надежность нерезервированных систем: для систем из последовательных элементов ВБР всей системы будет равно произведению ВБР всех элементов, а интенсивность отказов равно сумме интенсивности отказов каждого элемента. 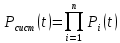 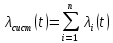 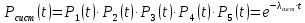 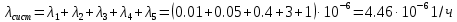 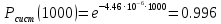 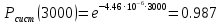 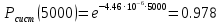 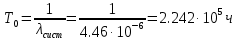 (примечание: по его расчетам Pсист (1000) =0.995, Pсист (3000) =0.988, Pсист (5000) =0.975. Я прорешал в маткаде, результат получается, как в формулах выше.) Вывод: на каждые 1000 машин вероятность выхода из строя при 1000 часах – 0.4%, на втором интервале 1.3%, на третьем интервале при 5000 часах – 2.2% (0.5%, 1.2%, 2.5% по его расчетам, соответственно). Даже при 5000 ч надежность системы достаточно высокая. Задача 3. Оценить надежность изделия на этапе технического проектирования. В техническом задании заданы следующие количественные показатели надежности: P(t)=0.9, σ=0.03, Кг=0.99, t=40 ч. Изделие состоит из 4 последовательно соединенных устройств, для которых надо принять экспоненциальный закон распределения. σ – среднеквадратичное отклонение от экспоненциального распределения. Расчет надежности производится по данным испытания, результаты которого приведены в таблице.
Решение. Для упрощения расчета разложим ex в ряд. 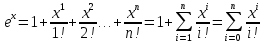 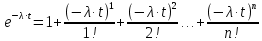 Достаточно двух первых слагаемых этого ряда, чтобы получить хорошую точность. 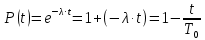 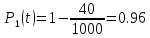 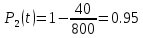 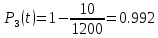 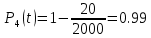 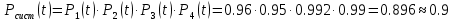 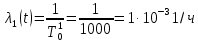 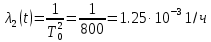 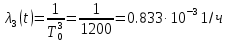 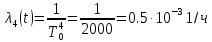 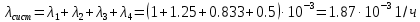 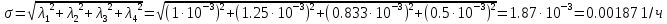 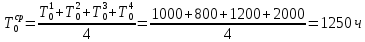 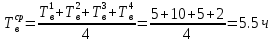 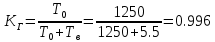 Вывод: полученные расчетные данные полностью удовлетворяют требованиям технического задания. Логарифмическое нормальное распределение Случайная величина X имеет логарифмическое нормальное распределение, если её натуральный логарифм имеет нормальное распределение. В нормальном распределении есть два параметра: 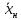 и и 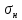 . Тогда основные характеристики: . Тогда основные характеристики: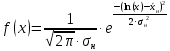 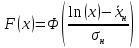 Ф(x) – функция Лапласа, табулированная, 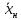 и и 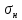 – параметры, оцениваемые по результатам испытаний. – параметры, оцениваемые по результатам испытаний.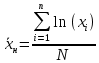 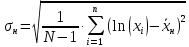 Квантилем распределения F(x) называется величина x, зависящая от p, являющаяся решением уравнения: 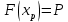 ВБР можно определить по таблицам для нормального распределения по значению квантиля: 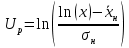 Как распределение положительных величин логарифмическое нормальное распределение несколько точнее, чем нормальное, описывает наработку до отказа деталей, например, по усталости. Его успешно применяют для описания наработки подшипников качения, электронных ламп и т.п. Характерной особенностью логарифмического нормального распределения является то, что интенсивность отказов λ сначала увеличивается, а затем уменьшается. 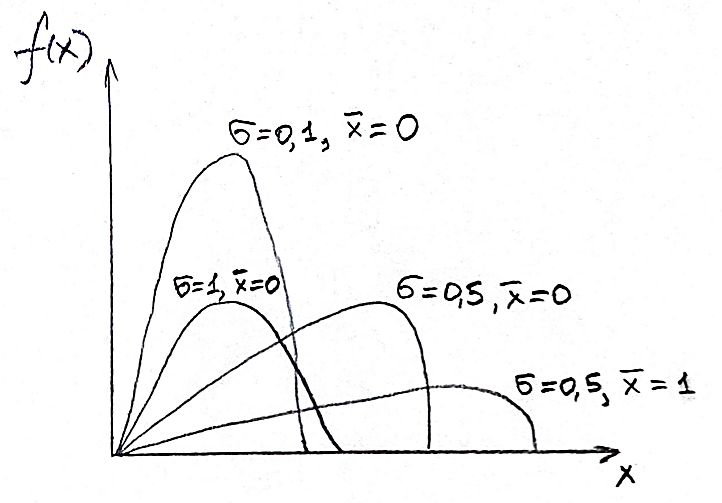 График f(x) для логнормального распределения 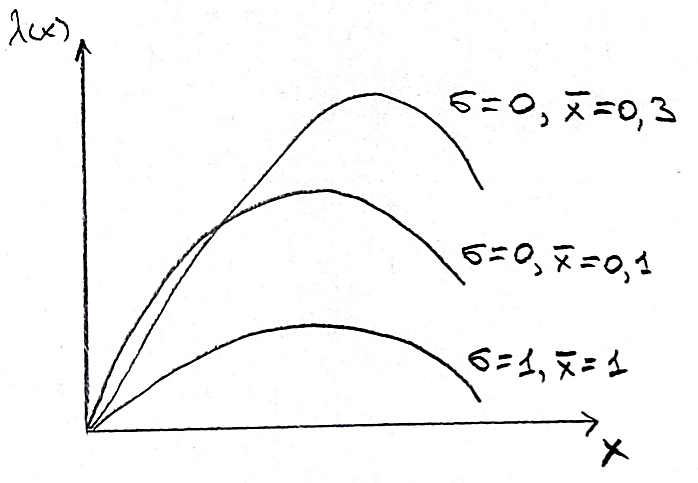 График λ(x) для логнормального распределения 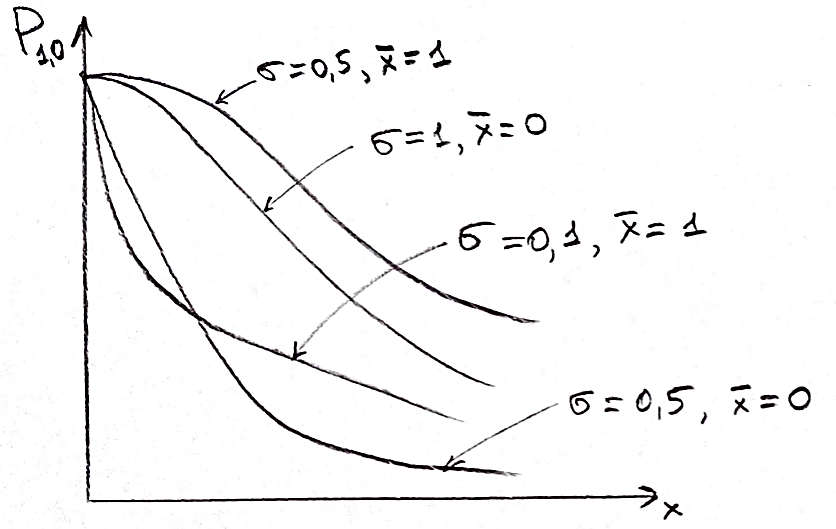 График P(x) для логнормального распределения Работать с логарифмическим нормальным распределением удобнее, если свести его к обычному нормальному распределению. Для этого следует рассматривать не случайную величину x, а её логарифм. Нормальное распределение (закон Гаусса) Закон Гаусса является одним из наиболее распространенным законом распределения погрешности. Функция распределения имеет вид: 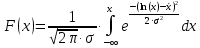 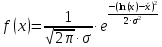 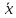 – центр группирования, характеризует распределение размеров. В простейшем случае равен 0. – центр группирования, характеризует распределение размеров. В простейшем случае равен 0.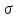 – характеризует кучность распределения размеров (погрешностей) около – характеризует кучность распределения размеров (погрешностей) около 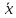 . Чем меньше, тем лучше (кучнее распределяются погрешности около центра группирования). . Чем меньше, тем лучше (кучнее распределяются погрешности около центра группирования).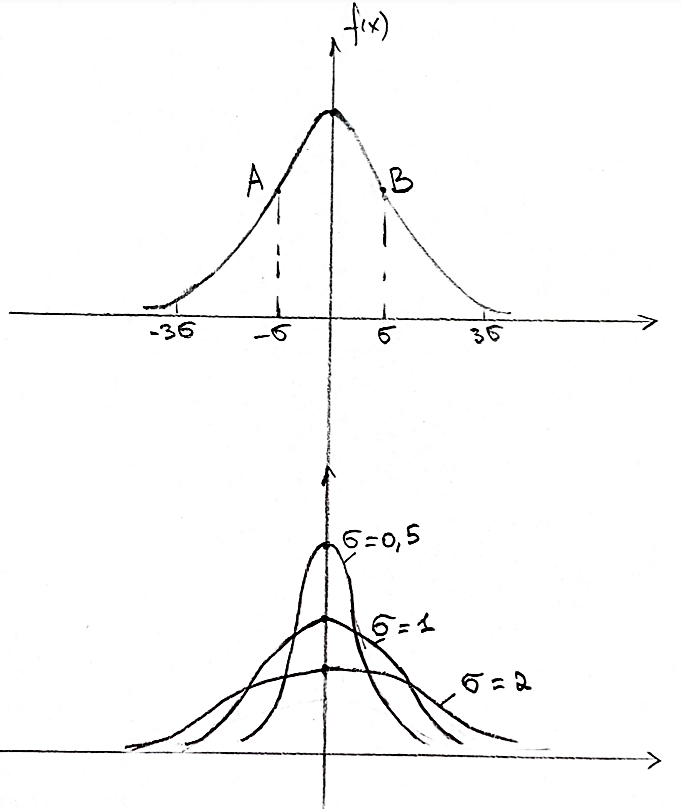 Особенности кривой Гаусса: Кривая симметрична относительно 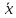 . .При 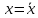 кривая имеет максимум, равный кривая имеет максимум, равный 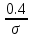 На расстоянии 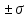 от от 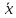 имеются точки А и B – точки перегиба, координаты которых примерно имеются точки А и B – точки перегиба, координаты которых примерно 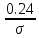 . .На расстоянии 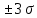 от вершины ветви так близки к оси абсцисс, что в этих пределах находится 99.73% всей площади. В связи с этим существует “усеченное” нормальное распределение. от вершины ветви так близки к оси абсцисс, что в этих пределах находится 99.73% всей площади. В связи с этим существует “усеченное” нормальное распределение.Если 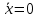 , а , а 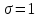 , то такое распределение называется стандартным. Тогда: , то такое распределение называется стандартным. Тогда: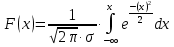 Таким образом, вероятность, что величина x находится в пределах от x1 до x2, равняется: 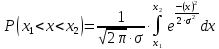 Проведём замену переменных 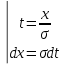 и разобьём этот интеграл на два (от и разобьём этот интеграл на два (от 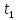 до 0, и от 0 до до 0, и от 0 до 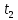 : :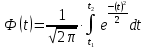 Такой интеграл называется нормальной функцией Лапласа, значения которой табулированы. Следовательно: 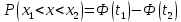 Если 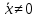 , то получаем: , то получаем: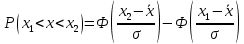 Теперь, если мы предположим, что 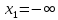 , то получим: , то получим: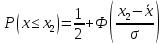 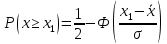 Поскольку 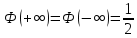 . .Нормальное распределение применяют для описания: Наработки машин до первого капитального ремонта. Описания износа и ресурсов деталей при нормальной эксплуатации. Задача 1. При измерении сопротивления установлено, что среднее значение этого сопротивление 5.5 кОм, а среднеквадратичное отклонение 1.5 кОм. Принимая нормальных закон распределения, найти вероятность появления сопротивления больше 10 кОм. Решение. 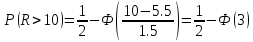 Из таблиц найдём, что 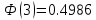 , тогда: , тогда: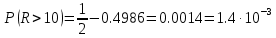 Задача 2. Оценить вероятность P(t) безотказной работы в течение t=1.5*104 ч изнашиваемого подвижного сопряжения, если ресурс по износу подчиняется нормальному распределению с параметрами 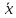 =4*104 ч, а =4*104 ч, а 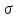 =104 ч. =104 ч.Решение. Для решения вычислим квантиль нормального распределения: 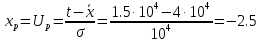 Далее по таблице определяем, какой вероятности соответствует найденный квантиль: 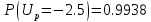 |
