руководство. Руководство по проведению практических занятий расчёт показателей надёжности сложных технических систем по статистическим данным
 Скачать 217.77 Kb. Скачать 217.77 Kb.
|
|
РУКОВОДСТВО ПО ПРОВЕДЕНИЮ ПРАКТИЧЕСКИХ ЗАНЯТИЙ «РАСЧЁТ ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ СЛОЖНЫХ ТЕХНИЧЕСКИХ СИСТЕМ ПО СТАТИСТИЧЕСКИМ ДАННЫМ» Учебная цель практических занятий: На примере решения задач закрепить и углубить теоретические знания по порядку расчета показателей надежности СТС по статистическим данным, полученным в процессе испытаний и эксплуатации. Время: 10 часов Материальное обеспечение: Тетрадь или листы формата А4 (10 шт); Листы миллиметровки формата А4 (3 шт); Калькулятор; Карандаш, линейка. Допускается использование вычислительной техники. Организационные указания: На самоподготовке, предшествующей практическим занятиям, студентам необходимо ИЗУЧИТЬ материал лекционных занятий по теме, а также данное руководство, обратив внимание на методику расчета показателей надежности СТС по статистическим данным, полученным в процессе испытаний и эксплуатации. К занятию БЫТЬ ГОТОВЫМ выполнить расчеты с использованием калькулятора по определению единичных показателей надежности СТС. Решение задач проводится по вариантам каждым студентом в отдельности. Номер варианта выдаётся преподавателем. ИСПОЛНИТЬ на стандартных листах формата А4 отчет по выполненным заданиям. Форма титульного листа отчёта приведена в Приложении 1. В отчете должно быть отражено: номер задачи; краткая постановка каждой задачи; таблицы исходных данных для данного варианта; порядок расчета показателей надежности (с приведением всех промежуточных расчётов); графики показателей, если это требуется в задании; результаты решения задач. ПОКАЗАТЕЛИ НАДЁЖНОСТИ И ПОРЯДОК ИХ РАСЧЁТА ПО СТАТИСТИЧЕСКИМ ДАННЫМ, ПОЛУЧЕННЫМ В ПРОЦЕССЕ ИСПЫТАНИЙ И ЭКСПЛУАТАЦИИНАДЁЖНОСТЬ — свойство объекта сохранять во времени способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования (ГОСТ 27.002-2015 «Надёжность в технике. Термины и определения»). Надёжность является сложным свойством, которое в зависимости от назначения объекта и условий его использования состоит из сочетаний свойств безотказности, ремонтопригодности, восстанавливаемости долговечности сохраняемости и готовности. БЕЗОТКАЗНОСТЬ - свойство объекта непрерывно сохранять способность выполнять требуемые функции в течение некоторого времени или наработки в заданных режимах и условиях применения. РЕМОНТОПРИГОДНОСТЬ - свойство объекта, заключающееся в его приспособленности к поддержанию и восстановлению состояния, в котором объект способен выполнять требуемые функции, путем технического обслуживания и ремонта. ВОССТАНАВЛИВАЕМОСТЬ - свойство объекта, заключающееся в его способности восстанавливаться после отказа без ремонта. ДОЛГОВЕЧНОСТЬ — свойство объекта, заключающееся в его способности выполнять требуемые функции в заданных режимах и условиях использования, технического обслуживания и ремонта до достижения предельного состояния. СОХРАНЯЕМОСТЬ - свойство объекта сохранять способность к выполнению требуемых функций после хранения и (или) транспортирования при заданных сроках и условиях хранения и (или) транспортирования. ГОТОВНОСТЬ – свойство объекта, заключающееся в его способности находиться в состоянии, в котором он может выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания и ремонта в предположении, что все необходимые внешние ресурсы обеспечены. Под показателем надёжности понимают количественную характеристику одного или нескольких свойств, составляющих надёжность объекта. Показатели надёжности могут быть единичными или комплексными. Единичный показатель надёжности характеризует одно из свойств, составляющих надёжность. К единичным показателям надёжности относятся показатели безотказности, ремонтопригодности и восстанавливаемости, долговечности, сохраняемости. Показатели безотказностиК показателям безотказности относятся: вероятность безотказной работы - 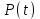 ; ;средняя наработка до отказа - 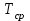 ; ;интенсивность отказов - 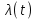 ; ;гамма - процентная наработка до отказа - 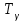 ср; ср;параметр потока отказов - 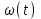 ; ;наработка между отказами - То ; гамма - процентная наработка между отказами - Тγо. Первые четыре показателя используются главным образом для оценки безотказности невосстанавливаемых объектов. Однако они могут использоваться и при оценке безотказности восстанавливаемых объектов до появления первого отказа. Последние три показателя относятся к восстанавливаемым объектам. ИНТЕНСИВНОСТЬ ОТКАЗОВ — условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник. Исходными данными для определения интенсивности отказов являются количество невосстанавливаемых объектов, находящихся в эксплуатации, и данные об отказах, полученные за определённый срок эксплуатации. По статистическим (опытным) данным интенсивность отказов может быть определена из соотношения: 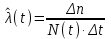 , (1) , (1)где: 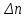 – число отказов в интервале – число отказов в интервале 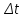 , ,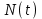 – число объектов, работоспособных к началу интервала – число объектов, работоспособных к началу интервала 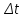 . .Если по рассчитанным таким образом частным значениям интенсивностей отказов для каждого промежутка времени 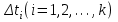 построить гистограмму и соединить эти значения плавной кривой, то получится функция построить гистограмму и соединить эти значения плавной кривой, то получится функция 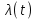 , характеризующая зависимость интенсивности отказов от времени работы (рис. 1). , характеризующая зависимость интенсивности отказов от времени работы (рис. 1).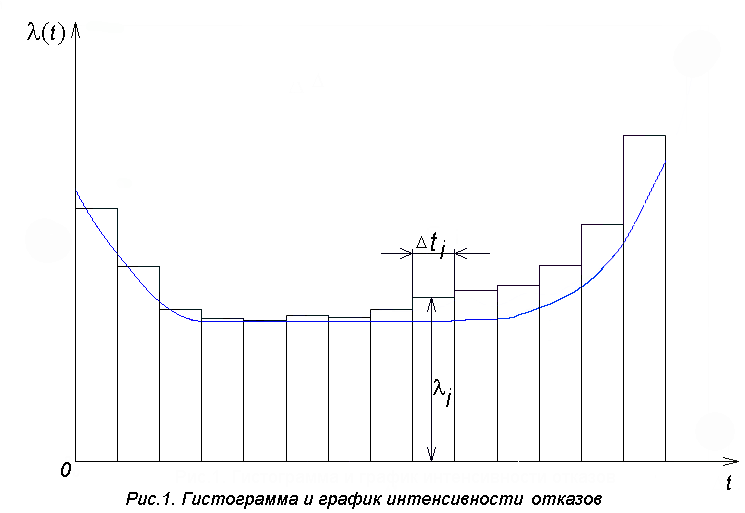 Иногда наряду с интенсивностью отказов определяют частоту отказов: 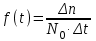 , (2) , (2)где 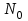 – число объектов, работоспособных в начальный момент времени (t=0). – число объектов, работоспособных в начальный момент времени (t=0).По полученным в процессе эксплуатации (испытаний) данным, пользуясь правилами математической статистики, строится гистограмма и график частот отказов (рис. 2). 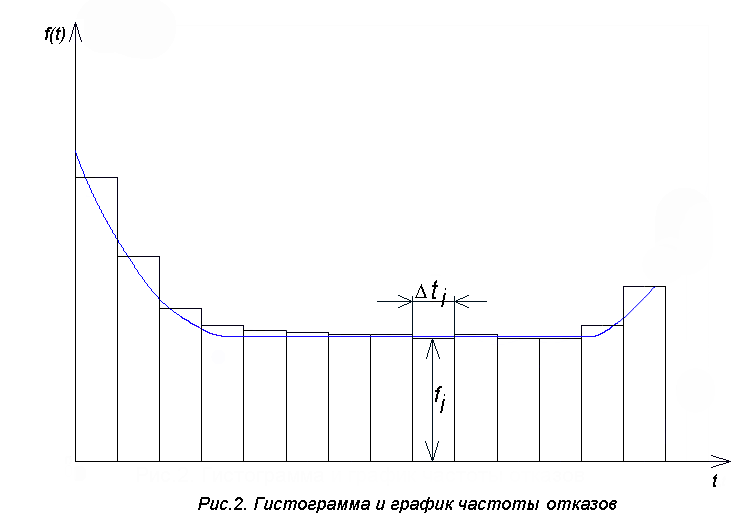 СРЕДНЯЯ НАРАБОТКА ДО ОТКАЗА определяется как математическое ожидание наработки объекта до отказа (ГОСТ 27.002-2015): 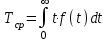 , (3) , (3)где 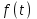 – плотность распределения наработки до отказа. – плотность распределения наработки до отказа.Оценка средней наработки до отказа по статистическим данным зависит от плана испытаний и закона распределения наработки до отказа. Так, если испытание ведётся до отказа всех объектов, то средняя наработка до отказа статистически определяется как отношение суммы наработок испытуемых объектов до отказа к количеству наблюдаемых объектов: 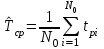 , (4) , (4)где: 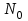 — число испытуемых объектов, — число испытуемых объектов,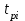 — наработка до отказа — наработка до отказа 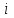 -го объекта. -го объекта.В практике эксплуатации, как правило, известны данные об отказах за определённое время 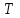 , когда из , когда из 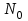 объектов, имеющихся к началу эксплуатации, откажет только n. Тогда для определения средней наработки до отказа при условии, что имеет место показательное (экспоненциальное) распределение наработки до отказа, следует пользоваться соотношением: объектов, имеющихся к началу эксплуатации, откажет только n. Тогда для определения средней наработки до отказа при условии, что имеет место показательное (экспоненциальное) распределение наработки до отказа, следует пользоваться соотношением: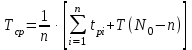 ; ; 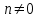 (5) (5)ВЕРОЯТНОСТЬ БЕЗОТКАЗНОЙ РАБОТЫ — вероятность того, что в пределах заданной наработки отказ объекта не возникнет (ГОСТ 27.002-2015). Иными словами, это вероятность того, что время безотказной работы объекта 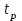 будет больше некоторого заданного времени будет больше некоторого заданного времени 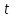 , т.e. , т.e.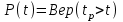 . .Практически величина вероятности безотказной работы определяется статистическим путём по информации об отказах за интересующий промежуток времени по формуле: 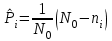 , (6) , (6)где: 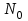 — число объектов, работоспособных к началу испытаний (началу заданного промежутка времени — число объектов, работоспособных к началу испытаний (началу заданного промежутка времени 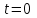 ), ),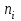 — число объектов, отказавших к концу заданного интервала времени за наработку — число объектов, отказавших к концу заданного интервала времени за наработку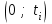 . .При значительном числе объектов статистическая вероятность 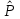 сходится по вероятности к сходится по вероятности к 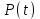 , т.е. в пределе равна истинному значению вероятности безотказной работы. , т.е. в пределе равна истинному значению вероятности безотказной работы.Надёжность объекта можно также оценивать вероятностью отказа 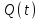 . Так как безотказная работа и отказ являются событиями противоположными и составляют полную группу несовместных событий, то: . Так как безотказная работа и отказ являются событиями противоположными и составляют полную группу несовместных событий, то: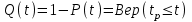 (7) (7)Статистическое значение вероятности отказа равно отношению числа отказов этих объектов за рассматриваемый промежуток времени к числу объектов, работоспособных к началу этого промежутка: 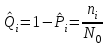 , (8) , (8)где: 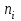 — число отказавших за наработку — число отказавших за наработку 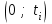 объектов из N0, находящихся в эксплуатации (на испытаниях). объектов из N0, находящихся в эксплуатации (на испытаниях).С помощью формул (6) и (8) можно построить графики 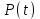 и и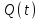 , примерный вид которых изображён на рисунке 3. , примерный вид которых изображён на рисунке 3.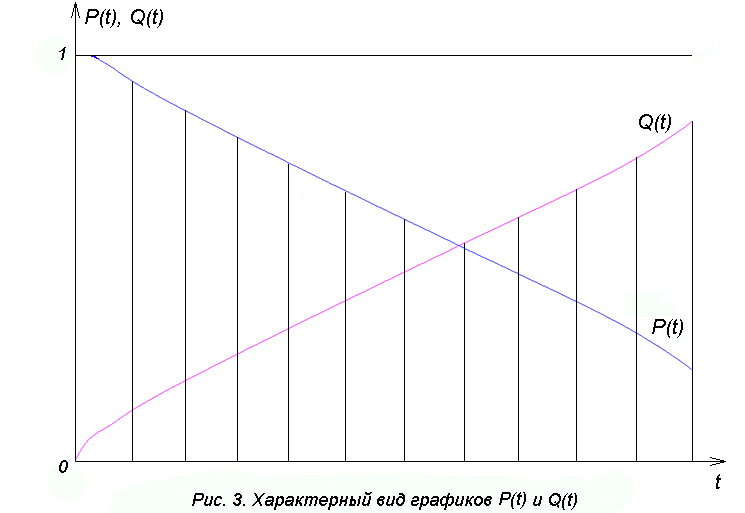 Кривая 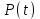 называется функцией надёжности, а кривая называется функцией надёжности, а кривая 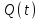 — функцией распределения наработки до отказа. Знание зависимости — функцией распределения наработки до отказа. Знание зависимости 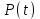 даёт возможность определить вероятность того, что объект, проработавший время даёт возможность определить вероятность того, что объект, проработавший время 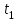 не откажет в течение последующего интервала времени от не откажет в течение последующего интервала времени от 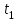 до до 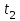 . В этом случае рассчитывается условная вероятность безотказной работы . В этом случае рассчитывается условная вероятность безотказной работы 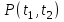 в течение наработки от в течение наработки от 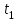 до до 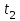 при условии, что при при условии, что при 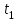 объект был работоспособен: объект был работоспособен: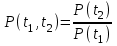 (9) (9)ПАРАМЕТР ПОТОКА ОТКАЗОВ - предел отношения вероятности возникновения отказа восстанавливаемого объекта за достаточно малый интервал времени к длительности этого интервала, стремящийся к нулю (ГОСТ 27.002 -2015). По статистическим данным об отказах, полученным в процессе эксплуатации, параметр потока отказов для каждого интервала наработки 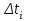 может быть рассчитан по формуле: может быть рассчитан по формуле: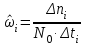 , (10) , (10)где: 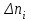 — число отказов — число отказов 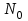 восстанавливаемых объектов на интервале восстанавливаемых объектов на интервале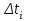 . .При показательном законе распределения времени наработки между отказами (т.е. на периоде нормальной эксплуатации, когда ω(t) = ω = const): вероятность безотказной работы на интервале времени ∆t: 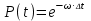 СРЕДНЯЯ НАРАБОТКА МЕЖДУ ОТКАЗАМИ - математическое ожидание наработки объекта между отказами (ГОСТ 27.002-2015). По статистическим данным, полученным в процессе эксплуатации, наработка на отказ определяется как отношение суммарной наработки восстанавливаемых объектов к суммарному числу отказов этих объектов: 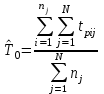 (11) (11)где: 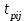 - - 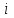 - я наработка - я наработка 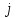 -го объекта, -го объекта,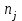 - число отказов j-го объекта, - число отказов j-го объекта,N - число однотипных объектов. Если производится оценка наработки на отказ одного объекта, то: 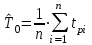 (12) (12)В процессе эксплуатации часто возникает задача априорной оценки показателей надёжности. Её можно решить, зная аналитические зависимости между различными показателями надёжности. Если известна функция 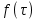 - плотность распределения вероятности наработки до отказа, то можно записать: - плотность распределения вероятности наработки до отказа, то можно записать: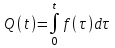 (13) (13)Тогда: 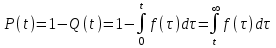 (14) (14)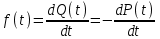 (15) (15)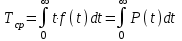 (16) (16)При показательном законе распределения плотность распределения: 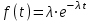 , (17) , (17)интенсивность отказов: 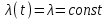 , (18) , (18)вероятность безотказной работы: 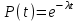 , (19) , (19)средняя наработка до отказа: 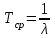 . (20) . (20)Показатели ремонтопригодности и восстанавливаемостиОсновными показателями ремонтопригодности и восстанавливаемости являются: вероятность восстановления работоспособного состояния: 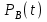 ; ;среднее время (до) восстановления работоспособного состояния: 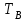 , ТДВ ; , ТДВ ;гамма – процентное время (до) восстановления: ТγВ, ТγДВ ; интенсивность восстановления работоспособного состояния: 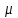 (t). (t).ВЕРОЯТНОСТЬ ВОССТАНОВЛЕНИЯ РАБОТОСПОСОБНОГО СОСТОЯНИЯ - вероятность того, что время (до) восстановления работоспособного состояния объекта не превысит заданное значение. Аналитически это можно записать так: 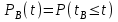 . (21) . (21)Отсюда следует, что  представляет собой функцию распределения времени восстановления. Если известна плотность распределения вероятности времени восстановления представляет собой функцию распределения времени восстановления. Если известна плотность распределения вероятности времени восстановления , то , то (22) (22)Если:  , то , то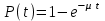 (23) (23)СРЕДНЕЕ ВРЕМЯ ВОССТАНОВЛЕНИЯ РАБОТОСПОСОБНОГО СОСТОЯНИЯ - математическое ожидание времени восстановления: 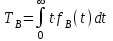 (24) (24)По статистическим данным, полученным в процессе эксплуатации, оценка среднего времени восстановления вычисляется по формуле: 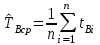 , (25) , (25)где: 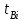 – время восстановления работоспособности после i-го отказа, – время восстановления работоспособности после i-го отказа,n – количество отказов за рассматриваемый срок эксплуатации. ИНТЕНСИВНОСТЬ ВОССТАНОВЛЕНИЯ - условная плотность вероятности восстановления работоспособного состояния объекта, определённая для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено. По данным об отказах за некоторый срок эксплуатации и при показательном законе распределения вероятности времени восстановления: 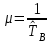 (26) (26)Показатели долговечностиК показателям долговечности относятся: средний ресурс - Трес; гамма - процентный ресурс - Тγрес; средний срок службы – Тср.сл.; гамма - процентный срок службы – Тγср.сл.. СРЕДНИЙ РЕСУРС (СРОК СЛУЖБЫ) — это математическое ожидание ресурса (срока службы). При наличии данных о ресурсе (сроке службе) N объектов статистическая оценка 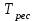 среднего ресурса (среднего срока службы) определяется по формуле: среднего ресурса (среднего срока службы) определяется по формуле: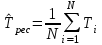 , (27) , (27)где 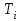 — ресурс i-го объекта. — ресурс i-го объекта.В случае усечённой выборки оценка среднего ресурса (среднего срока службы) определяется с учётом закона распределения ресурса (срока службы). При экспоненциальном законе распределения: 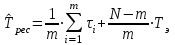 , (28) , (28)где: m – число объектов, выработавших ресурс за рассматриваемый срок эксплуатации 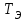 ; ;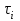 – выработанный ресурс i-го объекта. – выработанный ресурс i-го объекта.ГАММА - ПРОЦЕНТНЫЙ РЕСУРС - суммарная наработка, в течение которой объект не достигнет предельного состояния с вероятностью γ, выраженной в процентах. ГАММА - ПРОЦЕНТНЫЙ СРОК СЛУЖБЫ - календарная продолжительность эксплуатации, в течение которой объект не достигнет предельного состояния с вероятностью γ, выраженной в процентах. Эти показатели определяют из уравнения: 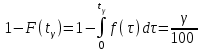 , (29) , (29)где: 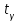 – гамма-процентный ресурс (гамма-процентный срок службы); – гамма-процентный ресурс (гамма-процентный срок службы);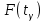 – функция распределения ресурса (срока службы); – функция распределения ресурса (срока службы);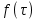 – плотность распределения вероятностей ресурса (срока службы). – плотность распределения вероятностей ресурса (срока службы).Показатели сохраняемостиК ним относятся: средний срок сохраняемости Тсохр. - математическое ожидание срока сохраняемости; гамма-процентный срок сохраняемости Тγсохр. - срок сохраняемости, достигаемый объектом с заданной вероятностью 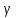 , выраженной в процентах; , выраженной в процентах;Показатели сохраняемости рассчитываются по формулам, аналогичным формулам (27), (28), (29). Приложение 1. Титульный лист отчёта по лабораторной работеМОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ) «МАИ» ОТЧЁТ по практическому занятию №1 «Расчет показателей надёжности невосстанавливаемых систем по статистическим данным» Вариант №13 Выполнил: студент группы 6о-416 Пономарёв Д.Е. Проверил: преподаватель Коробовский А.В. Москва 2021 г. |
