Отчет по ПРАКТ3 (Кириллов А.С) (НЧЛ). Практическая работа 3 Выполнение операции над нечеткими множествами. Направление подготовки

• Название: Практическая работа 3 Выполнение операции над нечеткими множествами. Направление подготовки
• Дата: 05.04.2022
• Размер: 0.73 Mb.
• Имя файла: Отчет по ПРАКТ3 (Кириллов А.С) (НЧЛ).docx
• Тип: Практическая работа; #442725

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное образовательное бюджетное учреждение высшего образования

«Вологодский государственный университет»

(ВоГУ)

НЕЧЕТКАЯ ЛОГИКА

1. 
   ПРАКТИЧЕСКАЯ РАБОТА №3
   
2. 
   «Выполнение операции над нечеткими множествами.»
   
3. 
   
   

Направление подготовки: 09.03.04 Программная инженерия
Направленность (профиль): Разработка программно-информационных систем
Форма обучения: очная

Институт: Математики, естественных и компьютерных наук
Кафедра: Автоматики и вычислительной техники

Группа: РПС-41
Студент: Кириллов А.С.
Руководитель: Суконщиков А.А.

Вологда

2021 г.

Цель работы

ознакомиться с наиболее распространенными логическими операциями над нечеткими множествами.
Теоретическая часть

Основные формулы операций над нечеткими множествами:

1. 
   Пересечение двух нечетких множеств
   

2. 
   Объединение двух нечетких множеств
   

3. 
   Разность двух нечетких множеств
   

4. 
   Симметрическая разность двух нечетких множеств
   

5. 
   Дополнение нечеткого множества
   

6. 
   Дизъюнктивная сумма двух нечетких множеств
   

7. 
   Алгебраическое пересечение двух нечетких множеств
   

8. 
   Алгебраическое объединение двух нечетких множеств
   

9. 
   Граничное пересечение двух нечетких множеств
   

10. 
    Граничное объединение двух нечетких множеств
    

11. 
    Драстическое пересечение двух нечетких множеств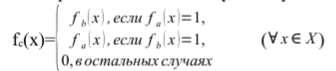
    

12. 
    Драстическое объединение двух нечетких множеств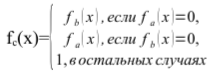
    

13. 
    Умножение нечеткого множества на число
    

14. 
    Возведение нечеткого множества в степень
    

15. 
    Концентрирование нечеткого множества
    

16. 
    Растяжение нечеткого множества
    

Определение центра тяжести фигур.

В SciLab нет специальных функций для определения центра тяжести

фигуры, поэтому будем использовать известные формулы для определения

центра тяжести треугольной и трапециевидной ФП.

Для определения координат центра тяжести треугольника необходимо:

1. 
   Сложить координаты «х» трех вершин треугольника.
   
2. 
   Сложите координаты «у» трех вершин треугольника.
   
3. 
   Разделить каждую сумму на 3
   
4. 
   Полученные х и у - координаты центра тяжести.
   

Центра тяжести равнобедренной трапеции лежит на прямой, соединяющей

центры оснований.
Определение коридора входных параметров ФП гаусса
Для определения коридора функции необходимо приравнять ее к

определенному значению Y1 и найти корни функции (значения х). Для этого

нужно написать функцию, которая будет возвращать значение ошибки между

искомым значением функции (Y1) и значением функции от произвольной

абсциссы хi, а затем найти значения абсцисс, при которых ошибка будет

минимальной – это можно реализовать командой fsolve().
Точка пересечения двух функций

Точку пересечения двух функций можно найти с помощью команды

fsolve(), используя равенство ординат функции в точке пересечения.

Практическая часть (общие задания):

1. 
   Построим график пересечения двух трапециевидных ФП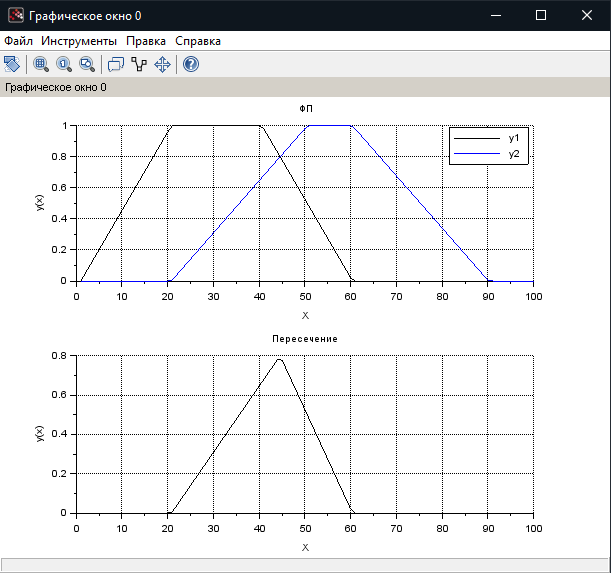
   

2. 
   Построим график драстического пересечения двух функций гаусса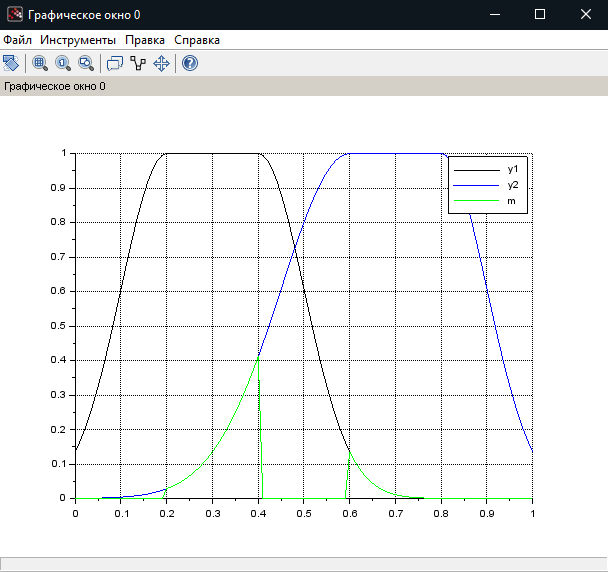
   

3. 
   Построим график драстического объединения двух функций гаусса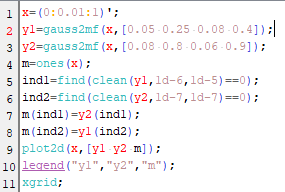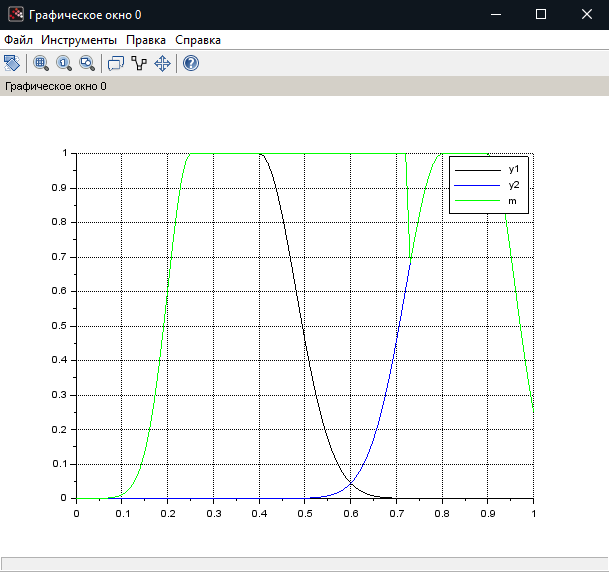
   

4. 
   Найдем центр тяжести треугольной функции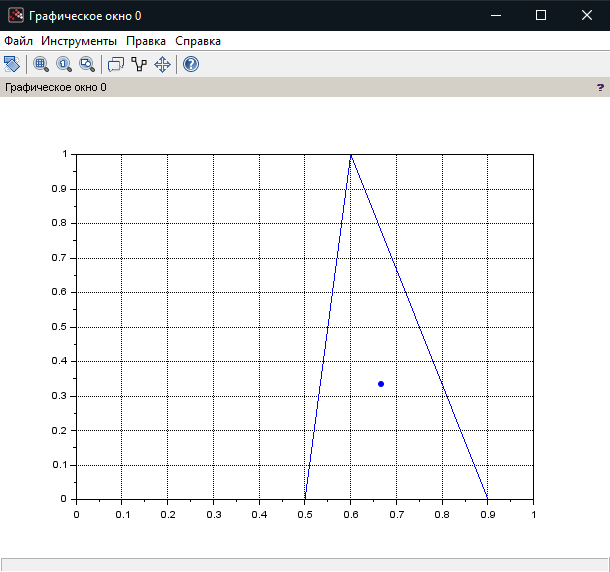
   

5. 
   Найдем центр тяжести равнобедренной трапеции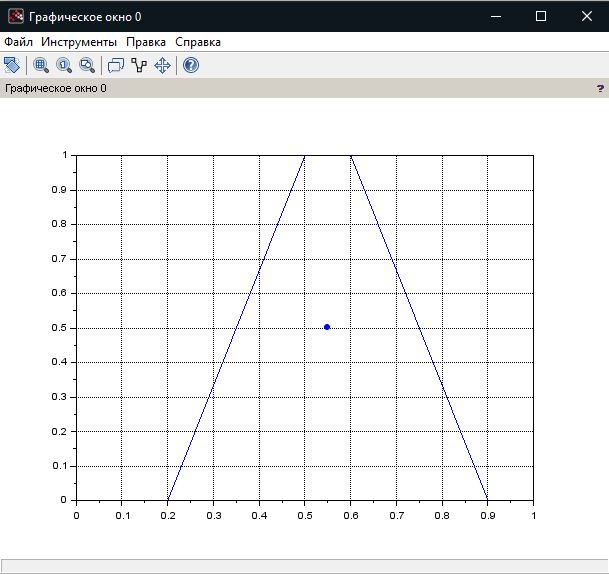
   

6. 
   Построим коридор входных параметров функций гаусса при y=0.8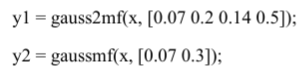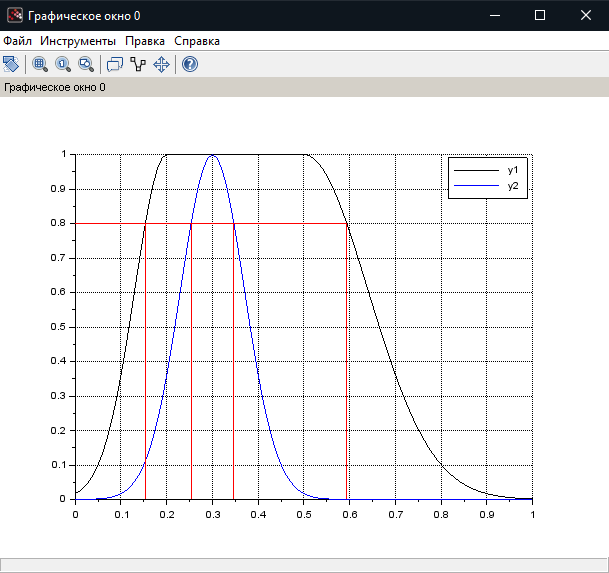
   

7. 
   Построим график пересечения двух функций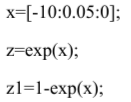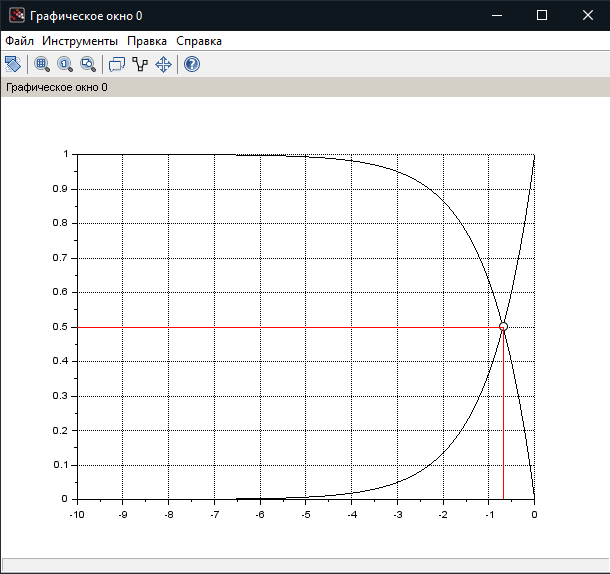
   

Индивидуальная часть (задания по вариантам):

Мой вариант – 5.
Задание №1.

В одном графическом окне (функция subplot) построить:

• 
  3 заданные по вариантам ФП
  
• 
  их пересечение
  
• 
  их объединение
  
• 
  их разность.
  

В итоге в одном графическом окне должно быть 4 графика



Решение:



Результат: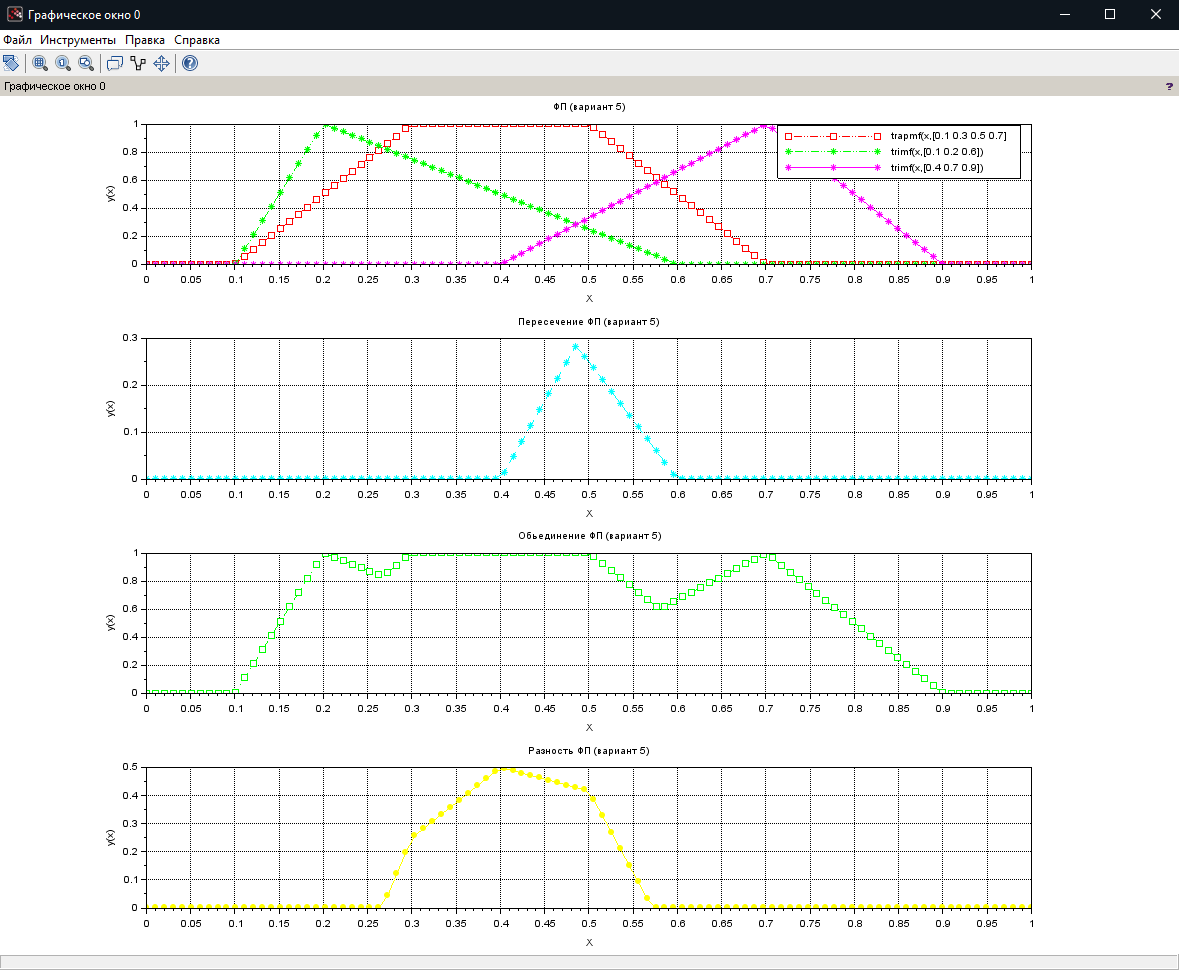



Задание №2.

В одном графическом окне (функция subplot) построить:

• 
  заданную ФП
  
• 
  дополнение
  
• 
  умножение на число a
  
• 
  концентрирование
  
• 
  растяжение
  
• 
  возведение в степень b
  

В итоге в одном графическом окне должно быть 6 графиков.



Решение:



Результат: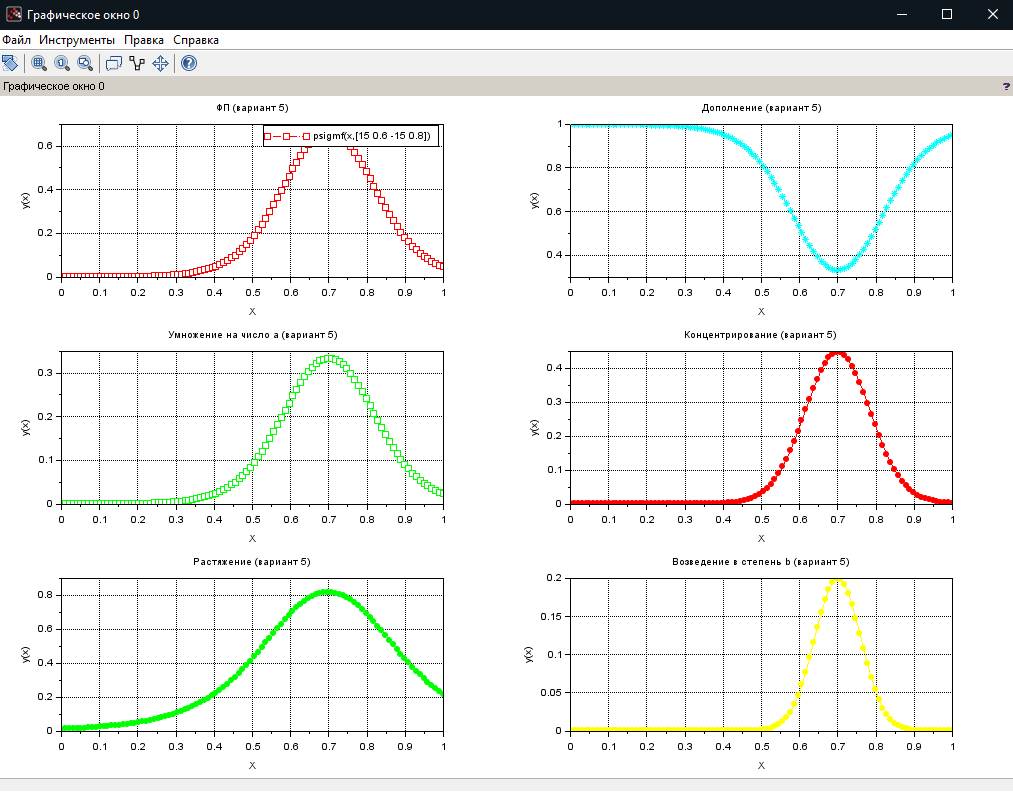



Задание №3.

В одном графическом окне (функция subplot) построить:

• 
  заданные ФП
  
• 
  симметрическую разность
  
• 
  дизъюнктивную сумму
  
• 
  алгебраическое пересечение
  
• 
  алгебраическое объединение
  
• 
  граничное пересечение
  
• 
  граничное объединение
  

В итоге в одном графическом окне должно быть 7 графиков.



Решение:



Результат: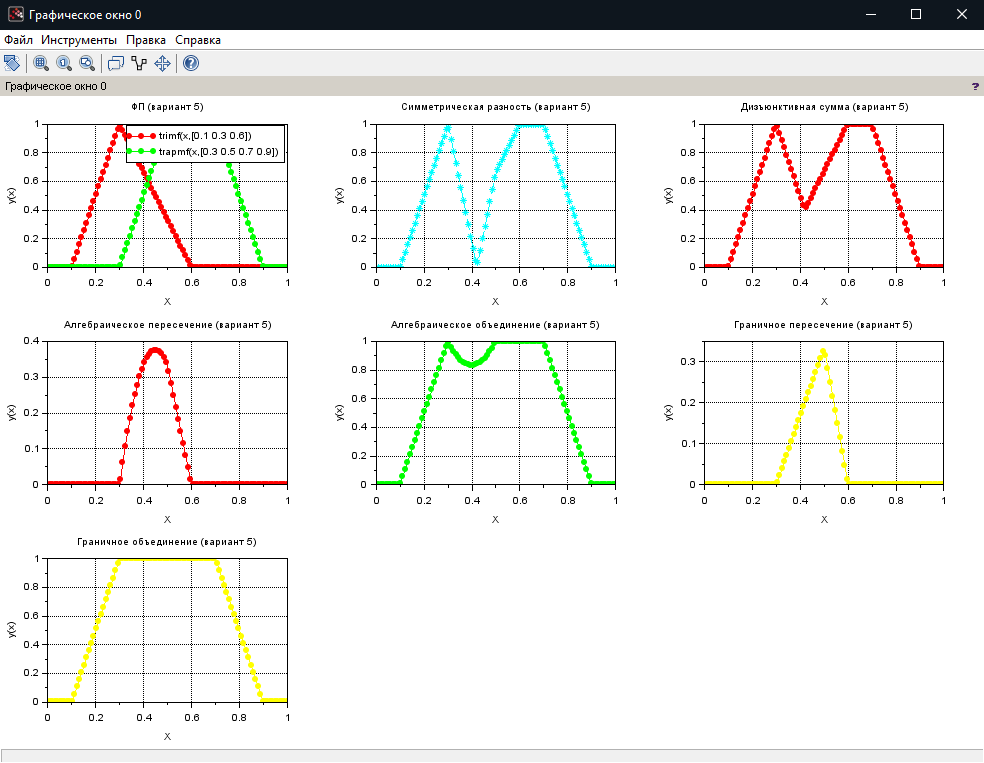



Вывод:

в результате выполнения практической работы мы успешно познакомились с наиболее распространенными логическими операциями над нечеткими множествами, в SciLab построили множество графиков, отражающих результаты этих операций.