Надежность-4. Практическая работа 4 Расчет надежности системы с постоянным резервированием Теоретические сведения
 Скачать 92.18 Kb. Скачать 92.18 Kb.
|
|
Практическая работа № 4 Расчет надежности системы с постоянным резервированием Теоретические сведения При постоянном резервировании резервные элементы 1,2,.... соединены параллельно с основным (рабочим) элементом в течение всего периода работы системы. Все элементы соединены постоянно, перестройка схемы при отказах не происходит, отказавший элемент не отключается. Вероятность отказа системы qc(t) определяется формулой 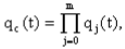 где qj(t) - вероятность отказа j-го элемента. Вероятность безотказной работы системы 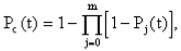 где Рj(t) - вероятность безотказной работы j-го элемента. Если Рj(t) =Р(t), j = 0, 1, . . . , m , то 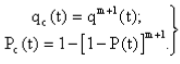 При экспоненциальном законе надежности отдельных элементов имеем 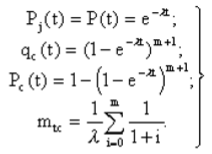 Резервирование называется общим, если резервируется вся система, состоящая из последовательного соединения n элементов. Схема общего резервирования показана на рис.4.2. Основная цепь содержит n элементов. Число резервных цепей равно m, т. е. кратность резервирования равна m. Определим количественные характеристики надежности системы с общим резервированием (резервные цепи включены постоянно). Запишем вероятность безотказной работы j - ой цепи где Рij(t), j = 0,1,2,...m; i=1,2,3,...,n - вероятность безотказной работы элемента Эij. Вероятность отказа j - ой цепи 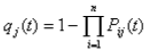 Вероятность отказа системы с общим резервированием 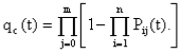 Вероятность безотказной работы системы с общим резервированием 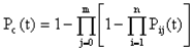 Частный случай: основная и резервные цепи имеют одинаковую надежность, т.е. Тогда 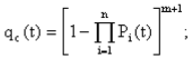 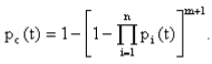 Рассмотрим экспоненциальный закон надежности, т. е. В этом случае формулы для qc(t) и Pc(t) примут вид 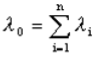 , ,где λ0 - интенсивность отказов цепи, состоящей из n элементов. Частота отказов системы с общим резервированием Интенсивность отказов системы с общим резервированием 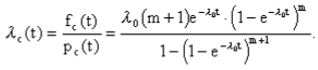 Среднее время безотказной работы резервированной системы 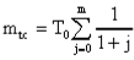 , ,где Т0 = 1/λ0 - среднее время безотказной работы нерезервированной системы. Задания на практическую работу Задача 1. Приемник состоит из трех. блоков: УВЧ, УПЧ и УНЧ. Интенсивности отказов этих блоков соответственно равны: λ1= 4·10-4 1/час; λ2 = 2,5·10-4 1/час; λ3 = 3·10-4 1/час. Требуется рассчитать вероятность безотказной работы приемника при t = 100 час для следующих случаев: а) резерв отсутствует; б) имеется общее дублирование приемника в целом. Задача 2. В радиопередатчике, состоящем из трех равнонадежных каскадов (n = 3) применено общее постоянное дублирование всего радиопередатчика. Интенсивность отказов каскада равна λ = 5·10-4 1/час. Определить Pc(t), T1c, fc(t), λc(t) радиопередатчика с дублированием. Задача 3. Радиоэлектронная аппаратура состоит из трех блоков I, II, III. Интенсивности отказов этих трех блоков соответственно равны: λ1, λ2, λ3. Требуется определить вероятность безотказной работы аппаратуры Pc(t) для следующих случаев: а) резерв отсутствует; б) имеется дублирование радиоэлектронной аппаратуры в целом. Задача 4. В телевизионном канале связи, состоящем из приемника и передатчика, применено общее дублирование. Передатчик и приемник имеют интенсивности отказов λп = 2·10-3 1/час, λпр = 1·10-3 1/час, соответственно. Схема канала представлена на рис. 1. Требуется определить вероятность безотказной работы канала Рc(t), среднее время безотказной работы Т1с, частоту отказов fc(t), интенсивность отказов λс(t). 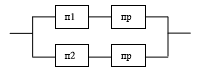 Рис. 1. Задача 5. Нерезервированная система управления состоит из n = 3000 элементов. Известна требуемая вероятность безотказной работы системы Рс(t) = 0,8 при t = 200 час. Необходимо рассчитать допустимую среднюю интенсивность отказов одного элемента, считая элементы равнонадежными, для того чтобы приближенно оценить достижение заданной вероятности безотказной работы при отсутствии профилактических осмотров в следующих случаях: а) резервирование отсутствует; б) применено общее ду6лирование. Задача 6. ИС состоит из двух блоков, соединенных последовательно и характеризующихся соответственно интенсивностями отказов λ1 = 120,54·10-6 1/час и λ2 = 185,66·10-6 1/час. Выполнено общее резервирование с неизменной нагрузкой всей системы (блока 1 и 2). Требуется определить вероятность безотказной работы Рс(t) ИС, среднее время безотказной работы Т1с, частоту отказов fc(t) и интенсивность отказов λс(t) ИС. Определить Рс(t) при t = 20 час. |
