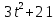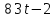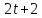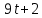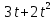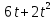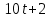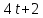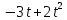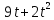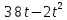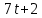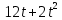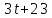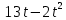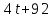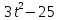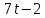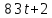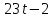лучший доклад о 5 работе. Практическая работа 5 Задача о вычислении пути Согласно физическому смыслу первой производной, производная функции в точке есть мгновенная скорость точки, т е.. Отсюда,. Интегрируя полученное равенство в пределах от t
 Скачать 67.73 Kb. Скачать 67.73 Kb.
|
|
практическая работа 5 1. Задача о вычислении пути Согласно физическому смыслу первой производной, производная функции в точке есть мгновенная скорость точки, т.е. 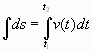 Тогда путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью 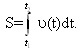 (1) (1)Пример 1. Скорость прямолинейного движения тела выражается формулой Решение. 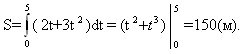 задача 1
время t совпадает с вашим вариантом. Пример 2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v Решение. Искомая величина есть разность расстояний, пройденных телами за 5 с. 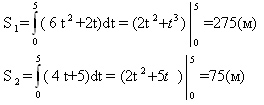 Таким образом, S=S1-S2= 275-75=200 (м). задача 2 Скорость первого тела берете из задачи 1, а скорость второго тела следующий вариант после вас То есть первый вариант берет свою скорость, а скорость второго берет из варианта 2 25 вариант берет скорость первого варианта. На каком расстояния друг от друга они окажутся через 10 с? 2. Задача о вычислении работы переменной силы Пусть материальная точка под действием силы F движется по прямой. Если действующая сила постояна, а пройденный путь равен s, то как известно из курса физики, работа А этой F вычисляется по формуле: А= F*s Работу переменной силы f(x) при перемещении по оси Оx материальной точки от x=a до x=b, находим по формуле (3): A= 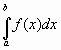 (2) (2)Решении задач на вычисление работы силы упругости, связанных с растяжением и сжатием пружин, основывается на законе Гука. По закону Гука сила F, растягивающая или сжимающая пружину, пропорциональная этому растяжению или сжатию, т.е. F=kx, где x – величина растяжения или сжатия, k – коэффициент пропорциональности. Пример 1. Сила упругости F пружины, растянутой на 11 = 0,05 м, равна 3H. Какую работу надо произвести, чтобы растянуть пружину на 12 =0,1 м? Решение. Подставив данные в формулу закона Гука, получим: 3=k*0.05, т.е. k=60, следовательно, сила упругости выражается соотношением F=60x. Найдем работу переменной силы по формуле (2), полагая, что а=0; b=0,1: A= 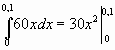 =0,3Дж =0,3Джзадача 3
3. Задача о силе давления жидкости Согласно закону Паскаля величина P давления жидкости на горизонтальную площадку вычисляется по формуле P=gphS, (4) Где g – ускорение свободного падения в м/с2; p– плотность жидкости в кг/м3; h – глубина погружения площадки в м; S – площадь площадки в м2. По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах. Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, у1 = f1(x) и у2=f2(х); система координат выбрана так, как указано на рисунке 1. Для решения задачи разобьем пластину на n частей (малых горизонт альных полосок) прямыми, параллельными поверхности жидкости (т.е. параллельными оси OY). На глубине х выделим одну из них и обозначим через f(x) ее длину, а через Найдем дифференциал dp этой функции. Тогда по закону Паскаля интегрируя полученное равенство в пределах от х = а до х = b, получим P=g 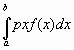 (3) (3)Пример Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м3), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 0,4 м x 0,7 м. Решение. Выберем систему координат так, чтобы оси Оy и Оx соответственно содержали верхнее основание и боковую сторону вертикальной стенки аквариума. Для нахождения силы давления воды на стенку воспользуемся формулой (3). Стенка имеет форму прямоугольника, поэтому 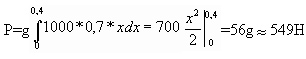 задача 4 Аквариум имеет форму прямоугольного параллелепипеда. Найдем силу давления воды (плотность воды 1000 кг/м3), наполняющей аквариум, на одну из его вертикальных стенок, размеры которой 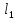 м x м x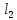 м м задача 5 Взять любую задачу ,где применяется определённый интеграл при решении задач. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||