Главная страница
Навигация по странице:

  • Цель работы

  • Краткие теоретические сведения

    		•

    Отыскание параметров линейной функции методом наименьших квадратов.. Практическая работа 6. Практическая работа 6 Отыскание параметров линейной функции методом наименьших квадратов (нмк) Цель работы


    Скачать 177 Kb.
    НазваниеПрактическая работа 6 Отыскание параметров линейной функции методом наименьших квадратов (нмк) Цель работы
    АнкорОтыскание параметров линейной функции методом наименьших квадратов
    Дата25.03.2022
    Размер177 Kb.
    Формат файлаdoc
    Имя файлаПрактическая работа 6.doc
    ТипПрактическая работа
    #416771

    Дисциплина: Метрология
    Практическая работа № 6
    Отыскание параметров линейной функции
    методом наименьших квадратов (НМК)
    Цель работы:

    Аналитически представить функциональную зависимость и подобрать формулу, описывающую результат эксперимента

    Краткие теоретические сведения:

    При выполнении эксперимента обязательно присутствуют случайные ошибки измерений. В связи с этим нет такой формулы, которая точно описывала бы все опытные значения. График искомой функции при этом не пройдёт через все точки. Сглаживание «шума» будет более точным и надёжным при значительном количестве экспериментальных данных.

    Эмпирическую формулу обычно выбирают из формул определённого типа, например: ; ; и др. Иными словами задача сводится к определению параметров формулы.

    Для простоты обозначим функциональную зависимость как . Параметры нельзя определить точно, так как функции содержат случайные ошибки. Речь идёт о получении «достаточно хороших» оценок искомых параметров. Метод наименьших квадратов позволяет это сделать. При этом предполагается, что измерения значений функции произведены независимо друг от друга, а ошибки измерений подчиняются нормальному закону распределения вероятностей.

    Если все измерения функции произведены с одинаковой точностью, то оценки параметров определяются из условия, чтобы сумма квадратов отклонений измеренных значений от расчётных принимала наименьшее значение.

    , (1)

    Если все измерения приведены с различными дисперсиями (неравноточны), но известны отношения дисперсий различных измерений, то тогда:

    , (2)

    где - все измерения, то есть

    , (3)

    Отыскание значений параметров , которые доставляют наименьшее значение функции сводится к решению системы уравнений:

    (4)

    Если в эмпирическую формулу (1) параметры входят линейно, то система уравнений (4) также будет линейной.

    Задача состоит в нахождении коэффициентов линейной зависимости, при которых функция двух переменных и принимает наименьшее значение.

    Пусть экспериментальные данные будут следующими:
    i = 1
    i = 2
    i = 3
    i = 4
    i = 5

    xi
    0
    1,2
    2,8
    4
    6

    yi
    2,2
    2,7
    2,9
    3,1
    3,3


    Составляется и решается система из двух уравнений с двумя неизвестными. Для решения находим прежде всего частные производные 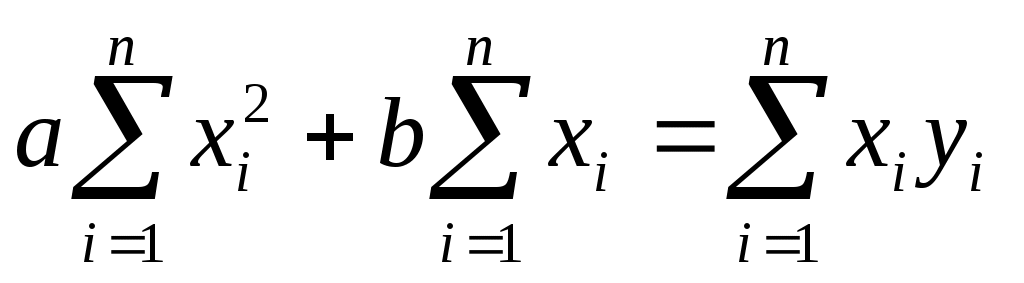по переменным a и b, приравнивая эти производные к нулю.








    Решая систему методом подстановки, находим коэффициенты a и b методом наименьших квадратов: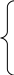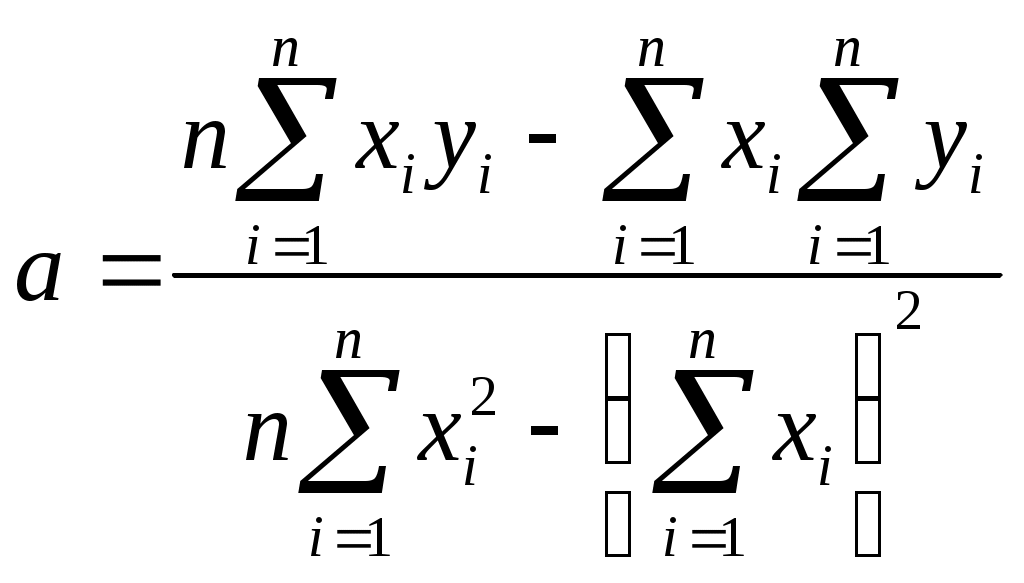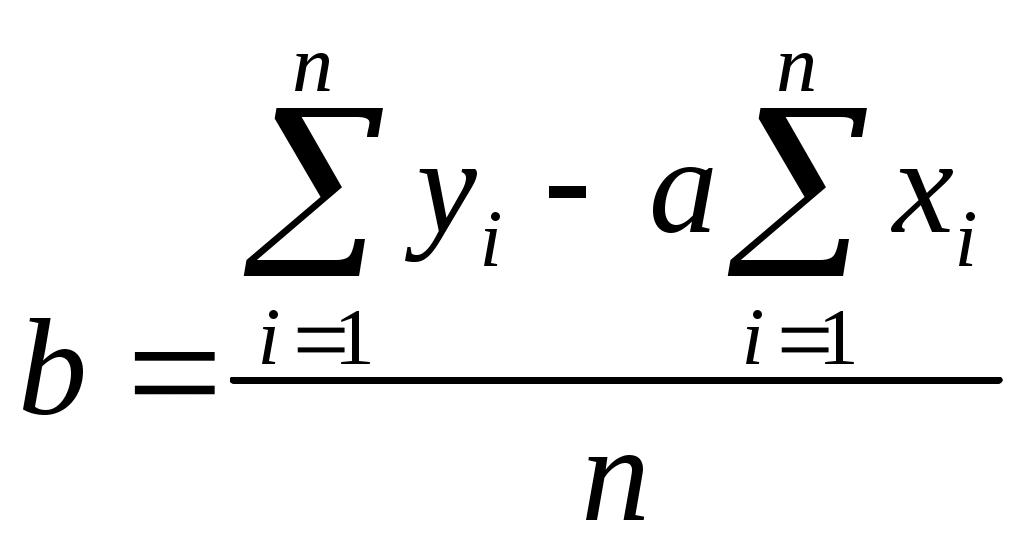





    Далее вычисляются все суммы отдельно, а результаты сводим в таблицу.












    xi
    0
    1,2
    2,8
    4
    6
    14

    yi
    2,2
    2,7
    2,9
    3,1
    3,3
    14,2

    xiyi
    0
    3,24
    8,12
    12,4
    19,8
    43,56



    0
    1,44
    7,84
    16,0
    36,0
    61,28


    Теперь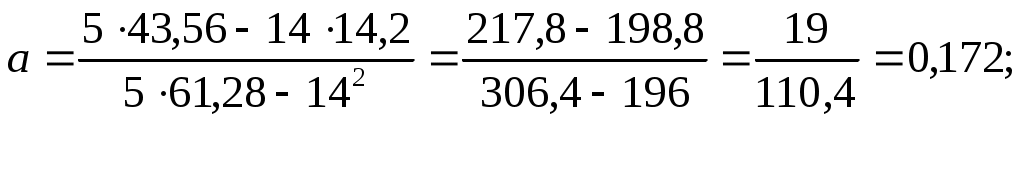







    Следовательно


    Необходимо:

    1. Составить и решить системы из двух уравнений с двумя неизвестными

    2. Определить коэффициенты a и b методом наименьших квадратов

    3. Выполнить табличное и графическое изображение результатов

    4. Оценить погрешность метода НМК

    5. Написать отчёт с выводом по работе


    Варианты заданий

    Номер варианта
    Значения функции и аргумента

    1
    2
    3
    4
    5

    x
    y
    x
    y
    x
    y
    x
    y
    x
    y

    1
    0
    2,1
    1,0
    2,4
    2,0
    2,6
    4,0
    2,8
    5,0
    3,0

    2
    0
    1,6
    0,8
    2,0
    1,8
    2,5
    3,6
    2,7
    4,8
    3,0

    3
    0,5
    1,9
    1,1
    2,3
    1,9
    2,6
    3,9
    3,0
    5,2
    3,1

    4
    1,0
    2,6
    1,2
    2,8
    2,2
    2,9
    4,0
    3,1
    5,5
    3,5

    5
    0,6
    2,0
    0,9
    2,2
    1,8
    2,4
    3,8
    2,9
    5,5
    3,4

    6
    0
    1,8
    1,1
    2,2
    2,1
    2,7
    4,1
    3,2
    5,3
    3,2

    7
    0,2
    2,0
    1,3
    2,4
    2,2
    2,8
    3,9
    3,1
    5,6
    3,5

    8
    0,4
    1,9
    1,0
    2,5
    2,1
    2,8
    4,2
    3,3
    5,7
    3,8

    9
    0
    1,7
    0,9
    2,1
    2,0
    2,6
    3,9
    3,1
    6,0
    3,7

    10
    0,7
    2,2
    1,3
    2,5
    2,4
    2,9
    4,1
    3,3
    5,8
    3,5

    написать администратору сайта