Практическая работа №6 Закон распределения ДСВ (2). Практическая работа 6 Закон распределения дискретной случайной величины

• Название: Практическая работа 6 Закон распределения дискретной случайной величины
• Дата: 11.10.2022
• Размер: 46.68 Kb.
• Имя файла: Практическая работа №6 Закон распределения ДСВ (2).docx
• Тип: Практическая работа; #726571

Практическая работа №6

Закон распределения дискретной случайной величины.
Цель работы: выработать умение решать задачи на запись распределения ДСВ, самостоятельной деятельности, вычислительных навыков.

Случайная величина – величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента.

Дискретной назовём случайную величину, возможные значения которой образуют конечное множество.

Законом распределения дискретной случайной величины называется правило, по которому каждому возможному значениюx_iставится в соответствие вероятностьp_i, с которой случайная величина может принять это значение, причём .

Пример. По мишени производится 4 независимых выстрела с вероятностью попадания при каждом выстреле р = 0,8. Требуется: а) найти закон распределения дискретной случайной величины х, равной числу попаданий в мишень; б) найти вероятности событий: 1  х  3; х > 3; в) построить многоугольник распределения.
Решение. а) Возможные значения случайной величины х: 0, 1, 2, 3, 4. Соответствующие вероятности вычисляем по формуле Бернулли: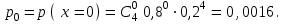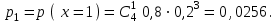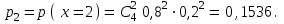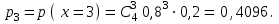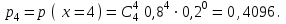











Закон распределения Х представится таблицей:

xi	0	1	2	3	4
pi	0,0016	0,0256	0,1536	0,4096	0,4096

Проверка: 0,0016 + 0,0256 + 0,1536 + 0,4096 + 0,4096 = 1.
б) Вероятность событий 1  х  3 и х > 3 равны:

р (1  х  3) = р ({1,2,3}) = р₁ + р₂ + р₃ = 0,0256 + 0,1536 + 0,4096 = 0,5888;

р( х > 3) = р ({4}) = р₄ = 0,4096.
Многоугольник рспределения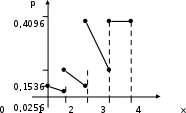



ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНУЮ РАБОТУ в соответствии со своим вариантом

Оформить решение по образцу примера 1
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 1

1. Дискретная случайная величина Х – число мальчиков в семьях с 5 детьми. Предполагая равновероятными рождения мальчика и девочки: а) найдите закон распределения Х; б) постройте многоугольник распределения; в) найдите вероятности событий: А – в семье не менее 2, но не более 3 мальчиков; В – не более 3 мальчиков; С – более одного мальчика.

2. Из коробки, в которой находятся 2 зелѐных, 2 чѐрных и 6 красных стержней для шариковой руки, случайным образом извлекаются 4 стержня. Построить закон распределения числа извлечѐнных стержней красного цвета. Найти вероятность того, что при этом красных стержней будет: а) не менее трѐх б) хотя бы один.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 2

1. С вероятностью попадания при одном выстреле 0,6 охотник стреляет по дичи до первого попадания, но успевает сделать не более 3 выстрелов. Дискретная случайная величина Х – число попаданий. а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3; 1 < x  3.

2. В магазин привезли 10 телевизоров, из которых 2 бракованных. В демонстрационный зал вынесли и подключили 4 телевизора. Событие Х состоит в следующем - «подключенный телевизор неисправен». Построить закон распределения. Найти вероятность того, что неисправных телевизоров будет: а) не менее трѐх б) хотя бы один.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 3

1. Дискретная случайная величина Х – число девочек в семьях с 6 детьми. Предполагая равновероятными рождения мальчика и девочки: а) найдите закон распределения Х; б) постройте многоугольник распределения; в) найдите вероятности событий: А – в семье не менее 2, но не более 3 девочек; В – не более 3 девочек; С – более одной девочки.

2. На пяти карточках написаны цифры 1, 2, 3, 4, 5. Две из карточек вынимаются наугад одновременно. Построить закон распределения суммы чисел, написанных на этих карточках. Найти вероятность того, что эта сумма будет: а) менее шести б) не менее пяти.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 4

1. Трое стрелков производят по одному выстрелу по мишени. Вероятность попадания первого стрелка равна р1=0,7, второго р2=0,8, третьего р3=0,9. Событие Х состоит в следующем «мишень поражена» (не уточняется сколько раз).

а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3; 1 < x  3.

2. Опыт состоит из четырѐх независимых подбрасываний двух одинаковых монет, т.е. выпадение герба и цифры равновозможные события. Построить ряд распределения числа одновременного выпадения двух цифр. Найти вероятность того, что это событие произойдѐт не менее трѐх раз.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 5

1. Баскетболист имеет четыре попытки забросить мяч в корзину. Он бросает мяч до первого попадания. Вероятность попасть в корзину в каждом броске одинакова и равна 0,7. Случайная величина X- количество выполненных баскетболистом бросков.
а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятность события х  1.

2. Производятся 4 независимых опыта, в каждом из которых с вероятностью 0,2; 0,4; 0,6; 0,8 соответственно может появиться случайное событие A. Построить закон распределения числа появлений события А. Найти вероятность того, что А произойдѐт не менее чем в половине опытов.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 6

1. В городе имеются 4 оптовые базы. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна 0,3. а) Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент. б) Постройте многоугольник распределения. в) Найдите вероятность события х  1.

2. Имеется набор из четырех карточек, на каждой из которых написана одна из цифр 1, 2, 3, 4. Из набора наугад извлекают карточку, затем ее возвращают обратно, после чего наудачу извлекают вторую карточку. Построить закон распределения случайной величины, равной сумме чисел, написанных на вынутых карточках. Найти вероятность того, что эта сумма: а) не превзойдет числа 4; б) будет не менее 6.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 7

1. Автоматизированную линию обслуживают 5 манипуляторов. При плановом осмотре их поочередно проверяют. Если характеристики проверяемого манипулятора не удовлетворяют техническим условиям, вся линия останавливается для переналадки. Вероятность того, что при проверке характеристики манипулятора окажутся неудовлетворительными, равна 0,3. а) Найдите закон распределения случайной величины Х, равной числу манипуляторов, проверенных до остановки линии. б) Постройте многоугольник распределения. в) Найти вероятность того, что до остановки линии будет проверено: а) не более двух манипуляторов б) более трѐх манипуляторов.

2. В коробке имеются 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекаются 3 карандаша. Найдите закон распределения случайной величины Х, равной числу красных карандашей в выборке. Найдите вероятность события 0 < x  2.

Практическая работа № 6 Закон распределения дискретной случайной величины.

Вариант 8

1. Наблюдение за районом осуществляется тремя радиолокационными станциями (РЛС). В район наблюдений попал объект, который обнаруживается любой радиолокационной станцией с вероятностью 0,2. Дискретная случайная величина Х – число РЛС, обнаруживших объект. а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3; 1 < x  3.

2. Стрелок, имеющий 4 патрона, стреляет последовательно по двум мишеням, до поражения обеих мишеней или пока не израсходует все 4 патрона. При попадании в первую мишень стрельба по ней прекращается, и стрелок начинает стрелять по второй мишени. Вероятность попадания при любом выстреле 0,8. Построить закон распределения числа поражѐнных мишеней. Найти вероятность того, что будет поражена хотя бы одна мишень.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 9

1. Ракетная установка обстреливает две удаленные цели. Вероятность попадания при каждом выстреле равна 0,6. Цель при попадании в нее уничтожается. Запуск ракет прекращается после уничтожения обеих целей или после использования имеющихся пяти ракет. а) Найдите закон распределения случайной величины Х, равной числу запущенных ракет. б) Постройте многоугольник распределения. в) Найти вероятность того, что при этом будет запущено: а) не более трех ракет; б) от двух до четырех ракет.

2. В коробке имеются 6 карандашей, из которых 4 красные. Из этой коробки наудачу извлекаются 3 карандаша. Найдите закон распределения случайной величины Х, равной числу красных карандашей в выборке. Найдите вероятность события 0 < x  2.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 10

1. Стрелок стреляет по мишени до трех попаданий или до тех пор, пока не израсходует все патроны, после чего прекращает стрельбу. Вероятность попадания при каждом выстреле равна 0,6. Дискретная случайная величина Х – число выстрелов, произведенных стрелком, если у стрелка имеется 5 патронов.

а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятность события при х  1.

2. Из урны, в которой было 4 белых и 2 черных шара, переложен один шар в другую урну, в которой находилось 3 черных шара и один белый. После перемешивания из последней урны вынимают 3 шара. Построить закон распределения числа черных шаров, вынутых из второй урны. Найти вероятность того, что из нее будет извлечено: а) по крайней мере, два черных шара; б) не более двух черных шаров.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 11

1. Баскетболист имеет три попытки забросить мяч в корзину. Он бросает мяч до первого попадания. Вероятность попасть в корзину в каждом броске одинакова и равна 0,35. Случайная величина Х – число попаданий в корзину.

а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3; 1 < x  3.

2. Имеются 5 ключей, из которых только один подходит к замку. Найдите закон распределения случайной величины Х, равной числу проб при открывании замка, если испробованный ключ в последующих опр

обованиях не участвует. Найдите вероятность события 0 < x  2.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 12

1. Центр управления полетами пытается установить радиосвязь с тремя искусственными спутниками Земли (ИСЗ), посылающими сигналы независимо друг от друга. Вероятность приема сигнала от каждого ИСЗ равна 0.5. Случайная величина X - количество принятых сигналов.

а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятность события х  1.

2 . Два носка выбираются случайным образом из ящика, в котором находится 5 коричневых и 3 зеленых. Найдите закон распределения числа коричневых носков. Найдите вероятность события x  1.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 13

1. Стрелок стреляет по мишени 5 раз. Вероятность промаха при каждом выстреле равна 0,2. Случайная величина Х – число промахов.

а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3; 1 < x  4.

2. В партии из 25 изделий 5 изделий имеют скрытый дефект. Определить закон распределения количества качественных деталей среди трѐх наудачу выбранных. Найдите вероятность события 1 < x  3.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 14

1. Вероятность изготовления нестандартной детали 0,1. Из партии контролер берет деталь и проверяет ее на стандартность. Если деталь оказывается нестандартной, то дальнейшие испытания прекращаются, а партия вся задерживается. Если же деталь окажется стандартной, то контролер берет следующую и т.д., но всего он проверяет не более 5 деталей. Найдите закон распределения случайной величины Х, равной числу стандартных деталей среди проверенных. б) Постройте многоугольник распределения. в) Найдите вероятность события 0 < x  2.

2. В партии из 8 деталей имеется 6 стандартных. Из этой партии наудачу взято 3 детали. а) Найдите закон распределения случайной величины, равной числу стандартных деталей в выборке. Найдите вероятность события х  1.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 15

1. На пути автомобиля 3 светофора, каждый из них автомобиль проезжает с вероятностью 0,6. Случайная величина Х – число светофоров, которые автомобиль проезжает до первой остановки.

а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 3; x  1; 1 < x  4.

2. Имеется набор из четырех карточек, на каждой из которых написана одна из цифр 1, 2, 3, 4. Из набора наугад извлекают карточку, затем ее возвращают обратно, после чего наудачу извлекают вторую карточку. Построить ряд распределения случайной величины, равной сумме чисел, написанных на вынутых карточках. Найти вероятность того, что эта сумма: а) не превзойдет числа 4; б) будет не менее 6.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 16

1. 3 стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка при одном выстреле – 0,6, для второго – 0,5, у третьего 0,8. Дискретная случайная величина Х –число попаданий в мишень. а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятность события 0 < x  2.

2. Дважды брошена игральная кость. Случайная величина Х равна сумме очков при первом бросании и числом очков при втором бросании. Найдите закон распределения Хи вероятность события при х  4.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 17

1. 2 стрелка стреляют по одной мишени, делая независимо друг от друга по 2 выстрела. Вероятность попадания в мишень для первого стрелка равна 0,9, для второго – 0,6. Найдите закон распределения случайной величины х, равной общему числу попаданий в мишень. б) Постройте многоугольник распределения. в) Найдите вероятность события 0 < x  2.

2. В вазе лежат 4 зеленых и 6 красных яблок. Из нее наугад берут 3 яблока. Событие Х состоит в следующем «попалось зеленое яблоко». Найдите закон распределения Хи вероятность события при х  2.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 18

1. Дискретная случайная величина Х – число мальчиков в семьях с 3 детьми. Предполагая равновероятными рождения мальчика и девочки: а) найдите закон распределения Х; б) постройте многоугольник распределения; в) Найдите вероятность события 0 < x  2.

2. Три ракетные установки стреляют каждая по своей цели независимо друг от друга до первого попадания, затем прекращают стрельбу. Каждая ракетная установка имеет две ракеты. Вероятность попадания одной ракеты для первой установки – 0,4, для второй – 0,5, для третьей – 0,6. Построить закон распределения числа ракетных установок, у которых осталась неизрасходованная ракета. Найти вероятность того, что будет хотя бы одна такая установка.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 19

1. Баскетболист имеет пять попыток забросить мяч в корзину. Он бросает мяч до первого попадания. Вероятность попасть в корзину в каждом броске одинакова и равна 0,2. Случайная величина Х – число попаданий в корзину.

а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 3; x  4; 2 ≤ x  4.

2. Рабочий обслуживает 4 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,7, для второго – 0,75, для третьего – 0,8, для четвертого – 0,9. Найдите закон распределения случайной величины Х, равной числу станков, которые не потребуют внимания рабочего. Найдите вероятность события 1 < x  3.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 20

1. С вероятностью попадания при одном выстреле 0,7 охотник стреляет по дичи до первого попадания, но успевает сделать не более 4 выстрелов. Дискретная случайная величина Х – число попаданий. а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3; 1 < x  3.

2. В магазин привезли 10 телевизоров, из которых 2 бракованных. В демонстрационный зал вынесли и подключили 3 телевизора. Событие Х состоит в следующем - «подключенный телевизор исправен». Построить закон распределения. Найти вероятность того, что исправных телевизоров будет: а) не менее двух; б) хотя бы один.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 21

1. Дискретная случайная величина Х – число мальчиков в семьях с 6 детьми. Вероятность рождения мальчика равна 0,52: а) найдите закон распределения Х; б) постройте многоугольник распределения; в) найдите вероятности событий: А – в семье не менее 3, но не более 5 мальчиков; В – не более 3 мальчиков; С – более одного мальчика.

2. Из коробки, в которой находятся 2 зелѐных, 2 чѐрных и 6 красных стержней для шариковой руки, случайным образом извлекаются 3 стержня. Построить закон распределения числа извлечѐнных стержней красного цвета. Найти вероятность того, что при этом красных стержней будет: а) не менее двух б) хотя бы один.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 22

1. Наблюдение за районом осуществляется четырьмя радиолокационными станциями (РЛС). В район наблюдений попал объект, который обнаруживается любой радиолокационной станцией с вероятностью 0,4. Дискретная случайная величина Х – число РЛС, обнаруживших объект. а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3.

2. Стрелок, имеющий 3 патрона, стреляет последовательно до поражения мишени или пока не израсходует все 4 патрона. При попадании в мишень стрельба прекращается. Вероятность попадания при любом выстреле 0,8. Построить закон распределения числа выстрелов. Найти вероятность того, что будет поражена хотя бы одна мишень.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 23

1. Баскетболист имеет три попытки забросить мяч в корзину. Он бросает мяч до первого попадания. Вероятность попасть в корзину в каждом броске одинакова и равна 0,4. Случайная величина X- количество выполненных баскетболистом бросков.
а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятность события х  1.

2. Производятся 4 независимых опыта, в каждом из которых с вероятностью 0,2; 0,4; 0,6; 0,8 соответственно может появиться случайное событие A. Построить закон распределения числа появлений события А. Найти вероятность того, что А произойдѐт не менее чем в половине опытов.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 24

1. Рабочий обслуживает 3 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,7, для второго – 0,75, для третьего – 0,8. а) Найдите закон распределения случайной величины Х, равной числу станков, которые не потребуют внимания рабочего б) Постройте многоугольник распределения. в) Найдите вероятность события 1 < x  3.

2. В партии из 20 деталей имеется 16 стандартных. Из этой партии наудачу взято 4 детали. а) Найдите закон распределения случайной величины, равной числу стандартных деталей в выборкеи вероятность события при х  3.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 25

1. 2 стрелка стреляют по одной мишени, делая независимо друг от друга по 2 выстрела. Вероятность попадания в мишень для первого стрелка равна 0,8, для второго – 0,5. Найдите закон распределения случайной величины Х, равной общему числу попаданий в мишень. б) Постройте многоугольник распределения. в) Найдите вероятность события 0 < x  2.

2. В вазе лежат 3 зеленых и 7 красных яблок. Из нее наугад берут 4 яблока. Событие Х состоит в следующем «попалось красное яблоко». Найдите закон распределения Хи вероятность события при х  2.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 26

1. Дискретная случайная величина Х – число мальчиков в семьях с 6 детьми. Предполагая равновероятными рождения мальчика и девочки: а) найдите закон распределения Х; б) постройте многоугольник распределения; в) найдите вероятности событий: А – в семье не менее 1, но не более 4 мальчиков; В – не более 2 мальчиков; С – более трех мальчиков.

2. Из коробки, в которой находятся 3 зелѐных, 4 чѐрных и 3красных стержней для шариковой руки, случайным образом извлекаются 3стержня. Построить закон распределения числа извлечѐнных стержней зеленого цвета. Найти вероятность того, что при этом зеленых стержней будет: а) не менее трѐх б) хотя бы один.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 27

1. В городе имеются 5 оптовых баз. Вероятность того, что требуемого сорта товар отсутствует на этих базах, одинакова и равна 0,2. а) Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент. б) Постройте многоугольник распределения. в) Найдите вероятность события х  3.

2. Производятся 3 независимых опыта, в каждом из которых с вероятностью 0,2; 0,4; 0,6 соответственно может появиться случайное событие A. Построить закон распределения числа появлений события А. Найти вероятность того, что А произойдѐт не менее чем в двух опытах.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 28

1. Ракетная установка обстреливает три удаленные цели. Вероятность попадания при каждом выстреле равна 0,7. Цель при попадании в нее уничтожается. Запуск ракет прекращается после уничтожения всех целей или после использования имеющихся пяти ракет. а) Найдите закон распределения случайной величины Х, равной числу запущенных ракет. б) Постройте многоугольник распределения. в) Найти вероятность того, что при этом будет запущено: а) не более трех ракет; б) от трех до пяти ракет.

2. В коробке имеются 10 карандашей, из которых 6 красные. Из этой коробки наудачу извлекаются 4 карандаша. Найдите закон распределения случайной величины Х, равной числу красных карандашей в выборке. Найдите вероятность события 1 < x  3.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 29

1. Дискретная случайная величина Х – число девочек в семьях с 6 детьми. Предполагая рождения девочки равной 0,52: а) найдите закон распределения Х; б) постройте многоугольник распределения; в) найдите вероятности событий: А – в семье не менее 2, но не более 3 девочек; В – не более 3 девочек; С – более одной девочки.

2. Рабочий обслуживает 3 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,7, для второго – 0,6, для третьего – 0,8. Найдите закон распределения случайной величины Х, равной числу станков, которые не потребуют внимания рабочего. в) Найдите вероятность события x  2.

Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 30

1. Баскетболист имеет три попытки забросить мяч в корзину. Он бросает мяч до первого попадания. Вероятность попасть в корзину в каждом броске одинакова и равна 0,65 Случайная величина X- количество выполненных баскетболистом бросков.
а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятность события х  2.

2. Производятся 4 независимых опыта, в каждом из которых с вероятностью 0,3; 0,4; 0,5; 0,7 соответственно может появиться случайное событие A. Построить закон распределения числа появлений события А. Найти вероятность того, что А произойдѐт не менее чем в трех опытах.
Практическая работа № 6 Закон распределения дискретной случайной величины.

Вариант 31

1. Наблюдение за районом осуществляется четырьмя радиолокационными станциями (РЛС). В район наблюдений попал объект, который обнаруживается любой радиолокационной станцией с вероятностью 0,2. Дискретная случайная величина Х – число РЛС, обнаруживших объект. а) Найдите закон распределения Х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3; 2 < x  4.

2. Стрелок, имеющий 3 патрона, стреляет последовательно по двум мишеням, до поражения обеих мишеней или пока не израсходует все 3 патрона. При попадании в первую мишень стрельба по ней прекращается, и стрелок начинает стрелять по второй мишени. Вероятность попадания при любом выстреле 0,9. Построить закон распределения числа поражѐнных мишеней. Найти вероятность того, что будет поражена хотя бы одна мишень.
Практическая работа № 6 Закон распределения дискретной случайной величины.
Вариант 32

1. Ракетная установка обстреливает три удаленные цели. Вероятность попадания при каждом выстреле равна 0,6. Цель при попадании в нее уничтожается. Запуск ракет прекращается после уничтожения обеих целей или после использования имеющихся пяти ракет. а) Найдите закон распределения случайной величины Х, равной числу запущенных ракет. б) Постройте многоугольник распределения. в) Найти вероятность того, что при этом будет запущено: а) не более четырех ракет; б) от двух до пяти ракет.

2. В коробке имеются 6 карандашей, из которых 3 красные. Из этой коробки наудачу извлекаются 4 карандаша. Найдите закон распределения случайной величины Х, равной числу красных карандашей в выборке. Найдите вероятность события 0 < x  2.