Зайнуллин И.Э.ПЭНП, 9 вариант. Практическая работа по дисциплине " Планирование эксперимента на производстве" Выполнил (а) студент 2 курса группы затм120
 Скачать 153.79 Kb. Скачать 153.79 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ» Отчёт Практическая работа по дисциплине “ Планирование эксперимента на производстве” Выполнил (а): студент 2 курса группы ЗАТм-1-20 Зайнуллин И.Э. Преподаватель: Сафаров И.М. г. Казань 2021 ВАРИАНТ 9 1. Провести статистическую обработку результатов удельного объема насыщенного водяного пара с доверительной вероятностью Р=0,95, если в опыте были получены следующие результаты:
Решение: Производим статистическую обработку результатов анализа давления насыщенного водяного пара в MS Excel.  Рисунок 1 – Исходные данные Математическая обработка включает расчет, как минимум, следующих статистических величин: - средняя арифметическая 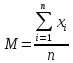 - среднеквадратичное отклонение единичного результата 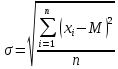 - стандартное отклонение среднеарифметической или ошибка средней арифметической из всех n повторностей 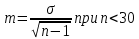 - достоверность средней арифметической 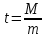 Полученные результаты представлены на рисунке 2. 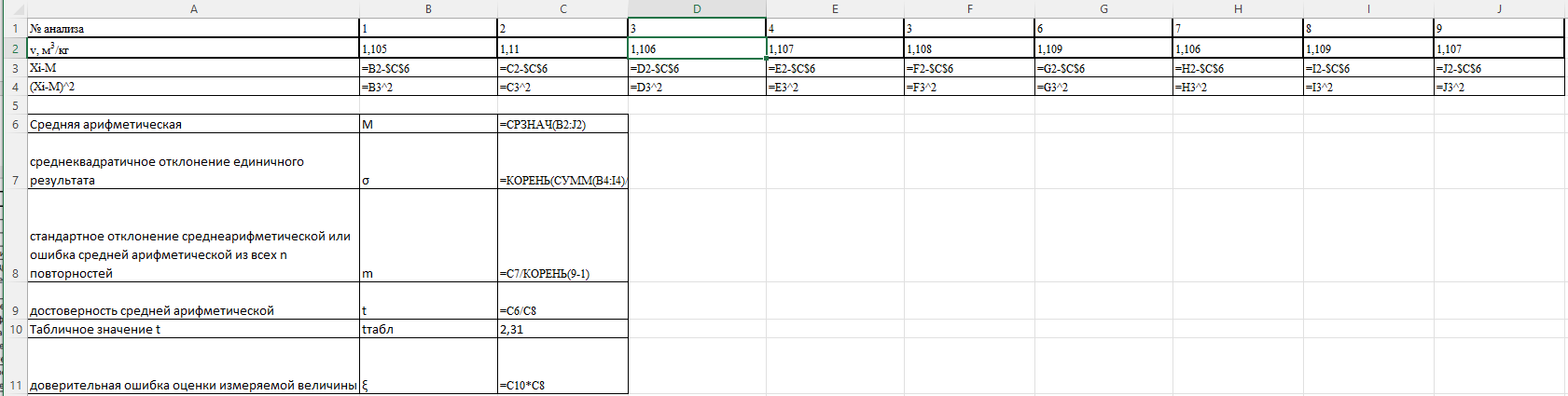 а 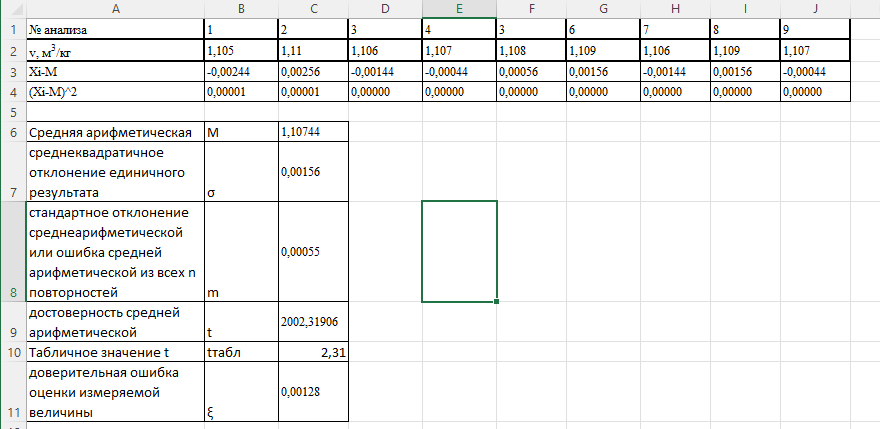 б Рисунок 2 – Полученные результаты расчетов а) таблица с отображением примененных формул б) таблица с числовыми результатами По прил. 4 при f=n-1=9-1=8 и Р=0,95 t=2,31. Так как tрасч>tтабл, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим. - доверительная ошибка оценки измеряемой величины 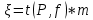 Таким образом, доверительный интервал выглядит следующим образом 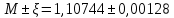 2. Установить корреляционную и функциональную зависимости между удельным объемом насыщенного водяного пара и температурой по данным, представленным в таблице:
Решение: Введем исходные данные  Рисунок 3 – Исходные данные Для установления корреляционной зависимости построим поле корреляции. Далее добавляем линию тренда, указываем уравнение регрессии и величину достоверности аппроксимации. 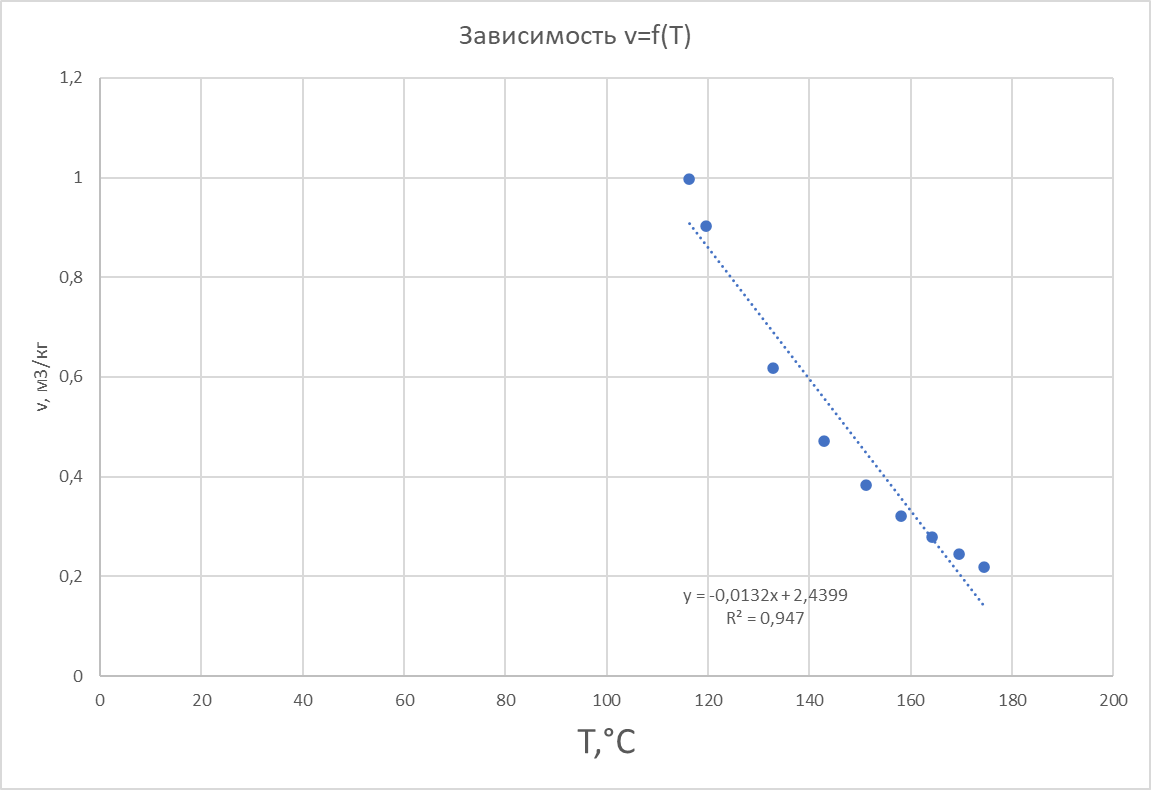 Рисунок 4 – График зависимости v=f(Т) Произведем необходимые расчеты для получения уравнения регрессии. 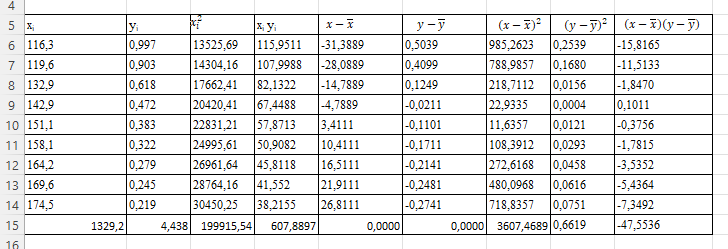 Рисунок 5 – Расчетные данные Найдем коэффициент корреляции: 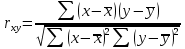 Найдем уравнение регрессии: 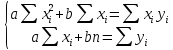 Отсюда 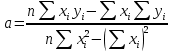 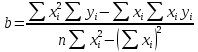 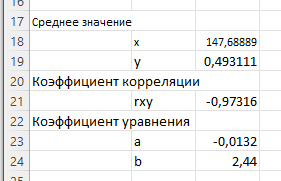 Рисунок 6 – Расчет коэффициентов Получаем уравнение регрессии: 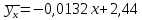 |
