Надежность_практическая работа вариант 1. Практическая работа _Надежность. Практическая работа по дисциплине Надежность электроснабжения Выполнил студент Горлов Евгений Геннадьевич Группа иб161582

• Название: Практическая работа по дисциплине Надежность электроснабжения Выполнил студент Горлов Евгений Геннадьевич Группа иб161582
• Анкор: Надежность_практическая работа вариант 1
• Дата: 16.07.2022
• Размер: 1.87 Mb.
• Имя файла: Практическая работа _Надежность.docx
• Тип: Практическая работа; #631799

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Институт высокоточных систем им. В.П. Грязева

Кафедра «Электроэнергетика»
Практическая работа

по дисциплине

«Надежность электроснабжения»
Выполнил студент

Горлов Евгений Геннадьевич

Группа: ИБ161582

Проверил

Ершов Сергей Викторович,

канд. техн. наук, доц.

Тула 2021 г.

Оглавление

Задача 1 3

Задача 2 4

Задача 3 5

Задача 4 6

Задача 5 8

Задачи 6 9

Задача 7 11

Задача 8 14

Список литературы 16

Задача 1

Система передачи электроэнергии потребителю состоит из генератора Г, повышающего трансформатора Т1, линии Л, понижающего трансформатора Т2.



Рисунок 1 – Схема к задаче 1

События отказа каждого элемента - независимые вероятности отказов: генератора Г - q_Г, трансформатора Т1 - q_Т1, линии Л – q_л, трансформатора Т2 - q_Т2. Определить вероятность того, что потребитель не получит электроэнергии из-за отказа системы.

Показатель	№вар	Вар7
Вер. отк. ген.	qГ	0,0035
Вер. отк. тр1	qТ1	0,00004
Вер. отк. лин.	qл	0,0035
Вер. отк. тр2	qТ1	0,00003

Решение

Вероятность события А – р(А) определим с использованием правила умножения для совместных событий - работы всех элементов системы - только в этом случае при последовательном соединении элементов возможна передача электроэнергии потребителю.

Определяем вероятность безотказной работы элементов схемы:

1. 
   генератора:
   

р_Г = (1 - q_Г);

р_Г = (1 - 0,0035) = 0,9965;

2. 
   трансформатора 1:
   

р_тр1 = (1 - q_тр1);

р_тр1 = (1 - 0,00004) = 0,99996;

3. 
   линии:
   

р_л = (1 - q_л);

р_л = (1 - 0,0035) = 0,9965;

4. 
   трансформатора 2:
   

р_тр1 = (1 - q_тр2);

р_тр2 = (1 - 0,00003) = 0,99997.

Определим вероятность безотказной работы, рассматривая систему как систему с последовательным соединением элементов:

Р_с = 1 - р_Г×р_тр1×р_л×р_тр2;

Р_с = 1 - 0,9965×0,99996×0,9965×0,99997 = 0,00349.

вероятность того, что потребитель не получит питания определяется как противоположное событие.

Задача 2

Потребитель получает электроэнергию по двум цепям линии электропередачи, сооружённым по разным трассам.



Рисунок 2 – Схема к задаче 2

Вероятность отказа каждой цепи qл. События отказов цепей независимые. Каждая цепь может пропустить 50% мощности, необходимой потребителю. Считая потребление мощности в течение всего рассчитываемого периода равным 100%, определить:

1. 
   Вероятность передачи 100% мощности.
   
2. 
   Вероятность передачи 50% мощности.
   
3. 
   Вероятность полной потери питания.
   

Таблица 2 - Исходные данные для задачи №2
Показатель	№вар	Вар7
Вер. отк. лин.	qл	0,0065

Решение

Определим вероятность безотказной работы линий электропередач:

р_л = 1- q_л;

р_л = 1 - 0,0065 = 0,9935.

1. 
   Осуществление передачи 100% мощности возможно только при одновременной работе двух цепей ЛЭП. Вероятность этого события соответствует параллельному соединению элементов:
   

р(100%) = р_л×р_л;

р(100%) = 0,9935×0,9935 = 0,98704.

2. 
   Передача 50% мощности возможна тогда, когда одна из цепей в рабочем состоянии, вторая - в состоянии отказа, всего таких случаев - 2.
   

р(50%) = р_л×q_л + р_л×q_л = 2р_л×q_л;

р(50%) = 2×0,9935×0,0065 = 0,0129155.

3. 
   Полная потеря питания возможна в случае одновременного отказа обеих цепей ЛЭП:
   

р(0%) = q_л×q_л = q_л²;

р(0%) = 0,0065^2 = 0,00004225.

Задача 3

Потребитель получает электроэнергию по двум цепям линии электропередачи, сооружённым по разным трассам.



Рисунок 3.1 – Схема к задаче 3

Вероятность отказа каждой цепи q_л. События отказов цепей независимые. При этом вероятность того, что потребителю требуется 100% мощности равна Р_треб(100%) = 0,5, a 50% мощности равна Р_треб(50%) = 0,5, т.е. определить вероятность передачи всей требуемой мощности, 50% мощности и полной потери питания.

Таблица 3 - Исходные данные для задачи №3
Показатель	№вар	Вар7
Вер. отк. лин.	qл	0,0065
Ртреб(100%)		0,5
Ртреб(50%)		0,5

Решение

Определим вероятность безотказной работы линий электропередач:

р_л = 1- q_л;

р_л = 1 - 0,0065 = 0,9935.

1. 
   Так как с вероятностью 0,5 потребителю требуется только 50% мощности то вероятность передачи всей мощности по сравнению с предыдущим случаем увеличивается на величину 0,5(2р_лq_л).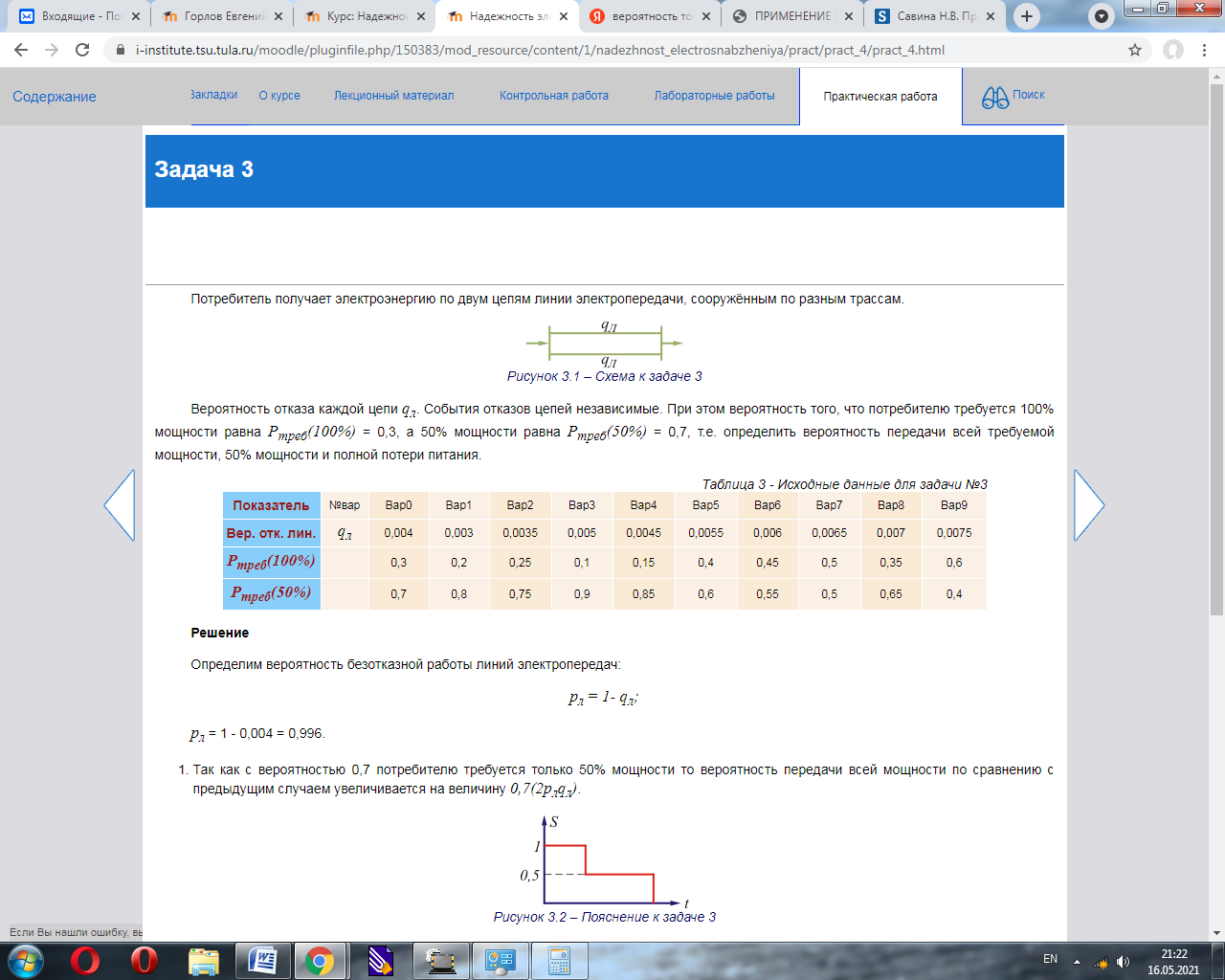
   

Рисунок 3.2 – Пояснение к задаче 3

Найдем 2р_лq_л:

2×0,9935×0,0065 = 0,0129155.

Найдем р_л².

р_л² = 0,9935^2 =0,98704.

р(100%) = р_л²(0,5 + 0,5) + 0,5×2р_лq_л;

р(100%) = 0,98704 (0,5 + 0,5) + 0,5×0,0129155= 0,993498.

2. 
   Вероятность передачи 50% мощности остаётся без изменения:
   

р(50%) = 2р_лq_л×0,5;

р(50%) = 2×0,9935×0,0065 ×0,5=0,006458.

3. 
   Вероятность полной потери питания:
   

р(0%) = q_л2;

р(0%) = 0,0065^2 = 0,00004225.

В этом случае, с учётом графика нагрузки, недоотпуск электроэнергии уменьшится.

Задача 4

Система передачи потребителю электроэнергии состоит из повышающего трансформатора Т1, двух независимых цепей линии электропередачи, двух понижающих трансформаторов Т2.



Рисунок 4 – Схема к задаче 4

События отказов всех элементов системы независимы. Вероятности отказов и пропускные способности элементов приведены в таблице 4.

Таблица 4 - Исходные данные к задаче 4
Показатель	№вар	Вар7
Вер. отк. тр1	qтр1	0,0065
Вер. отк. лин.	qл	0,05
Вер. отк. тр2	qтр2	0,005

Для всех вариантов:

Элемент	Т1	ЛЭП	Т2
Пропускная способность %	100	100/100	50/50

Считая потребление мощности неизменным и равным 100%, определить р(100%), р(50%), р(0%).

Решение

Определяем вероятности безотказной работы элементов схемы.

р_тр1 = 1- q_тр1;

р_тр1 = 1 - 0,0065 = 0,9935;

р_л = 1 - q_л;

р_л = 1 - 0,05 = 0,95;

р_тр2 = 1 - q_тр2;

р_тр2 = 1 - 0,005 = 0,995;

1. 
   Передача всей мощности возможна, если работает трансформатор Т1, хотя бы одна из цепей ЛЭП и два трансформатора Т2:
   

р(100%) = р_тр1(1 - q_л²) р_тр2²;

р(100%) = 0,9935 (1 - 0,05²) 0,995= 0,986061.

2. 
   Передача 50% мощности возможна, если повреждён один трансформатор Т2, работает один трансформатор Т1, и хотя бы одна цепь ЛЭП:
   

р(50%) = р_тр1(1 - q_л2)²_ртр2q_тр2;

р(50%) = 0,9935* (1 - 0,05²)*0,995*0,005= 0,0049303.

3. 
   Полная потеря питания:
   

р(0%) = q_тр1 + q_л² + q_тр2;

р(0%) = 0,0065 + 0,05² + 0,005²=0,009025.

Задача 5

Промышленное предприятие получает электроэнергию от двух источников питания ИП-1 и ИП-2. Вероятность безотказной работы первого источника р_ИП1 = 0,96, второго р_ИП2 = 0,95. Схема электроснабжения с указанием пропускных способностей элементов и вероятностей отказов приведена ниже.

Таблица 5 -  Исходные данные к задаче 5
Показатель	№вар	Вар7
Вер. отк. тр1	qтр1	0,0065
Вер. отк. тр2	qтр2	0,0045
Вер. отк. тр3	qтр3	0,005
Вер. отк. тр4	qтр4	0,0045
Вер. отк. лин.I	qлI	0,05
	qлI/ qлII	0,1
Вер. отк. лин.I	qлII	0,05
Вер. без.раб.ИП1	рИПI	0,96
Вер. без.раб.ИП1	рИПII	0,95

Для всех вариантов:

Элемент	Т1	Т2	Т3	Т4	ЛЭП-1	ЛЭП-2
пропускная способность, %	100%	100%	100%	100%	100/100	100%

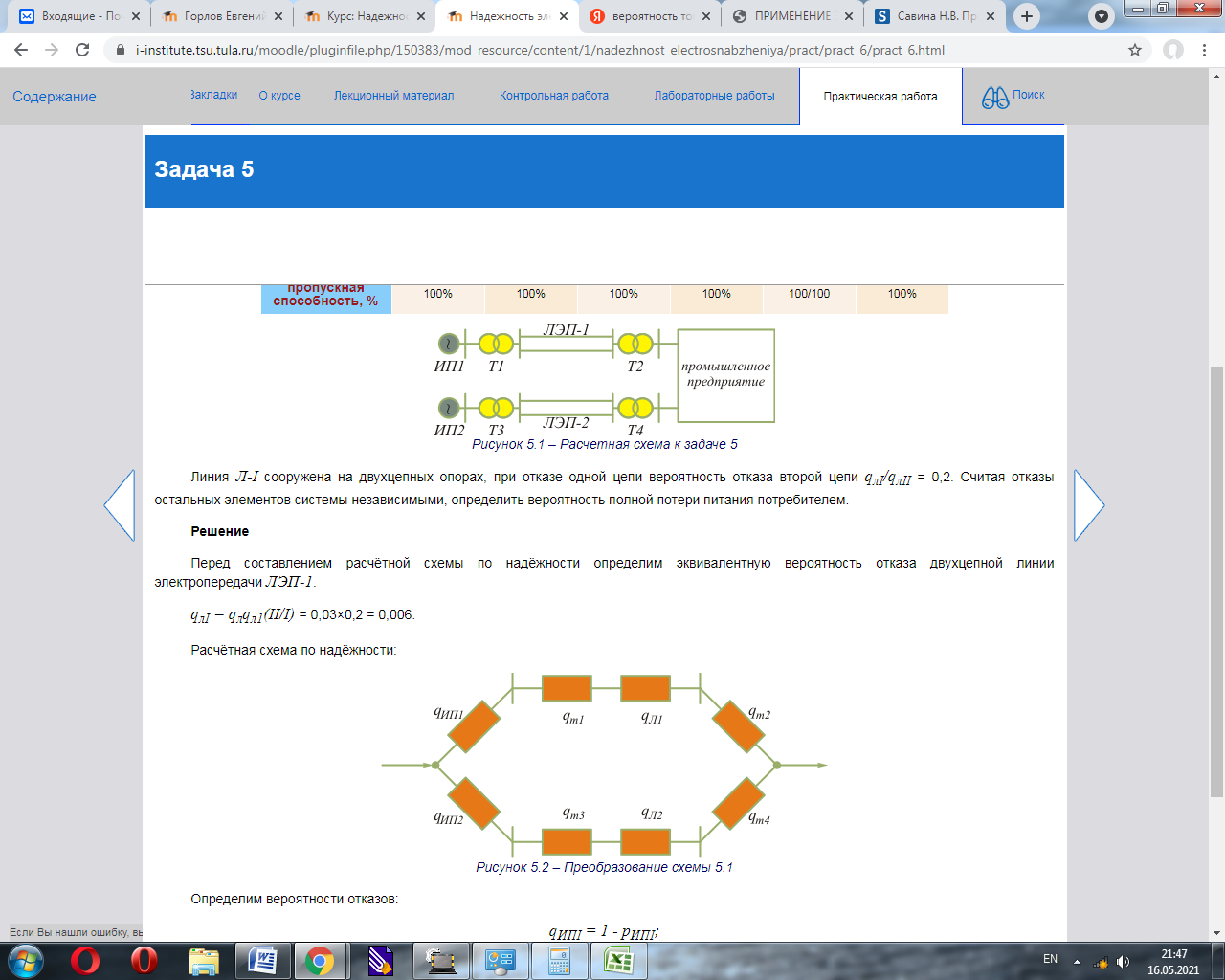Линия Л-I сооружена на двухцепных опорах, при отказе одной цепи вероятность отказа второй цепи q_лI/q_лII = 0,1. Считая отказы остальных элементов системы независимыми, определить вероятность полной потери питания потребителем.

Решение

Перед составлением расчётной схемы по надёжности определим эквивалентную вероятность отказа двухцепной линии электропередачи ЛЭП-1.

q_лI = q_лq_л1(II/I) = 0,05×0,1 = 0,005.

Расчётная схема по надёжности:



Рисунок 5.2 – Преобразование схемы 5.1

Определим вероятности отказов:

q_ИПI = 1 - p_ИПI;

q_ИПI = 1 - 0,96 = 0,04;

q_ИП2 = 1 - p_ИП2;

q_ИПI = 1 - 0,95 = 0,05;

Вероятность полной потери питания:

q_c = р(0%) = (q_ИПI + q_тр1 + q_л + q_тр2)(q_ИП2 + q_тр3 + q_л² + q_тр4);
q_c = (0,04 + 0,0065+ 0,005 + 0,0045)*(0,05 + 0,005 + 0,05 + 0,0045) = 0,006132.

Задачи 6

Система передачи электроэнергии состоит из пяти линий передачи (см. рисунок 6.1) и двух понижающих трансформаторов в пункте 4.

Пропускная способность каждой линии относительно узла нагрузки п.4 составляет 100% мощности, передаваемой в п.4.

Пропускная способность каждого понижающего трансформатора 50%. вероятность отказовых состояний линии А, В, С, Д, Е соответственно q_A = 0,19, q_B = 0,05, q_C = 0,3,q_Д = 0,12, q_Е = 0,02, каждого трансформатора Т1 q_тр1 = 0,0025.

Считая график потребления мощности в п.4 постоянным и неизменным в течение рассматриваемого периода времени, определить вероятность передачи 100%, 50%, и 0% мощности потребителю п.4.

Таблица 6 -  Исходные данные к задаче 6
Показатель	№вар	Вар7
Вер. отк. А	qА	0,19
Вер. отк. В	qВ	0,05
Вер. отк. С	qС	0,3
Вер. отк. D	qD	0,12
Вер. отк. Е	qE	0,02
Вер. отк. тр1	qтр1	0,0025

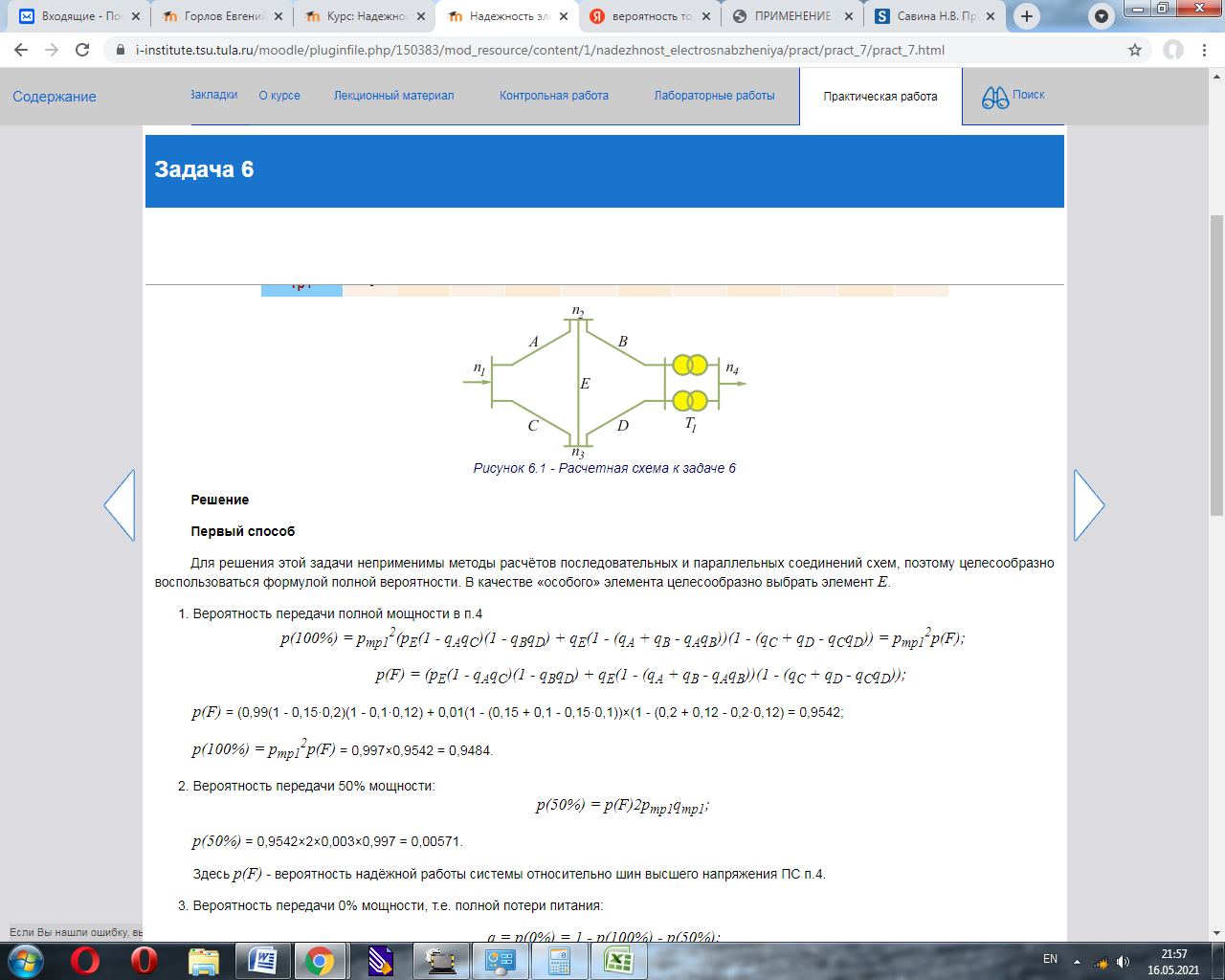Рисунок 6.1 - Расчетная схема к задаче 6

Решение

Для решения этой задачи неприменимы методы расчётов последовательных и параллельных соединений схем, поэтому целесообразно воспользоваться формулой полной вероятности. В качестве «особого» элемента целесообразно выбрать элемент Е.

1. 
   Вероятность передачи полной мощности в п.4
   

p(100%) = р_тр1²(р_Е(1 - q_Аq_С)(1 - q_Вq_D) + q_Е(1 - (q_А + q_В - q_Аq_В))(1 - (q_С + q_D - q_Cq_D)) = р_тр1²р(F);

р(F) = (р_Е(1 - q_Аq_С)(1 - q_Вq_D) + q_Е(1 - (q_А + q_В - q_Аq_В))(1 - (q_С + q_D - q_Cq_D));

р(F) = (0,98(1 - 0,19·0,3)(1 - 0,05·0,12) + 0,02(1 - (0,19 + 0,05 - 0,19·0,05))×(1 - (0,3 + 0,12 - 0,3·0,12) = 0,928075;

p(100%) = р_тр1²р(F) = 0,9965*0,928075= 0,924827.

2. 
   Вероятность передачи 50% мощности:
   

p(50%) = р(F)2p_тр1q_тр1;

p(50%) = 0,928075*2*0,0025*0,9965 = 0,004624.

Здесь р(F) - вероятность надёжной работы системы относительно шин высшего напряжения ПС п.4.

3. 
   Вероятность передачи 0% мощности, т.е. полной потери питания:
   

q = p(0%) = 1 - p(100%) - p(50%);

q = 1 - 0,924827- 0,004624 = 0,070549.

Задача 7

Двухцепная линия электропередачи напряжением 110 кВ, длиной l, км, сооружённая на одних опорах, имеет следующие показатели надёжности среднее значение параметра потока отказов одной цепи λ₀₁, 1/км·год, второй цепи λ₀₂, 1/км·год. Доля отказов линии, приводящих к отключению двух цепей по одной причине равна γ. Среднее время аварийного восстановления одной цепи t_в1, час, двух цепей t_в2, час. Время планового простоя одной цепи t_пр, час/год при четырех отключениях в год. Пропускная способность каждой цепи - 100% передаваемой мощности.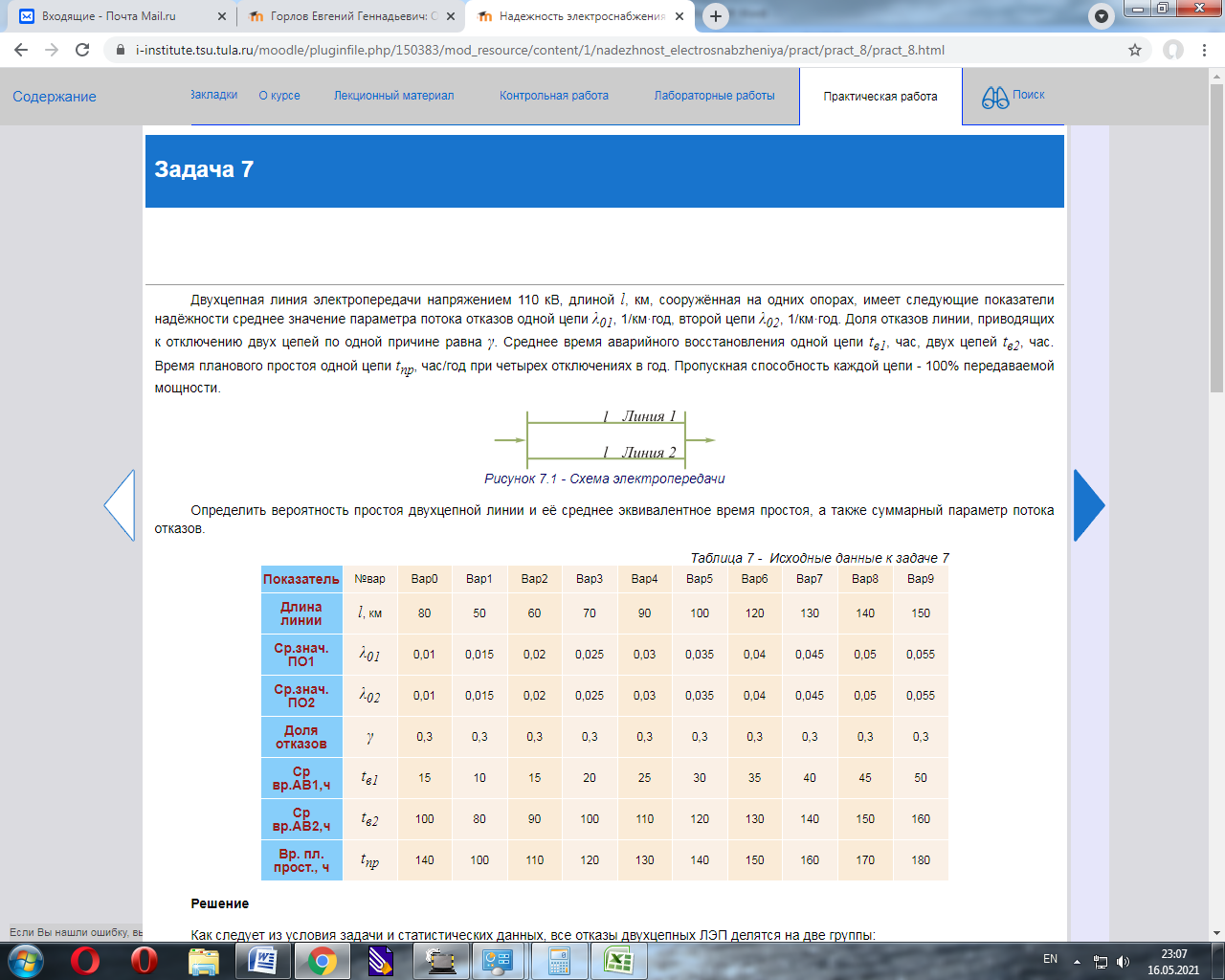



Рисунок 7.1 - Схема электропередачи

Определить вероятность простоя двухцепной линии и её среднее эквивалентное время простоя, а также суммарный параметр потока отказов.

Таблица 7 -  Исходные данные к задаче 7
Показатель	№вар	Вар7
Длина линии	l, км	130
Ср.знач. ПО1	λ01	0,045
Ср.знач. ПО2	λ02	0,045
Доля отказов	γ	0,3
Ср вр.АВ1,ч	tв1	40
Ср вр.АВ2,ч	tв2	140
Вр. пл. прост., ч	tпр	160

Решение

Как следует из условия задачи и статистических данных, все отказы двухцепных ЛЭП делятся на две группы:

1. 
   отказы только одной цепи;
   
2. 
   одновременные отказы обеих цепей, вызванные одной и той же причиной.
   

Поэтому при таких условиях задачи двухцепная ЛЭП в расчёте надёжности должна представляться в виде двух параллельно соединённых элементов, характеризующих параллельные отказы каждой цепи ЛЭП, и одного последовательно соединённого элемента, характеризующего одновременный отказ обеих цепей, вызванный одной и той же причиной.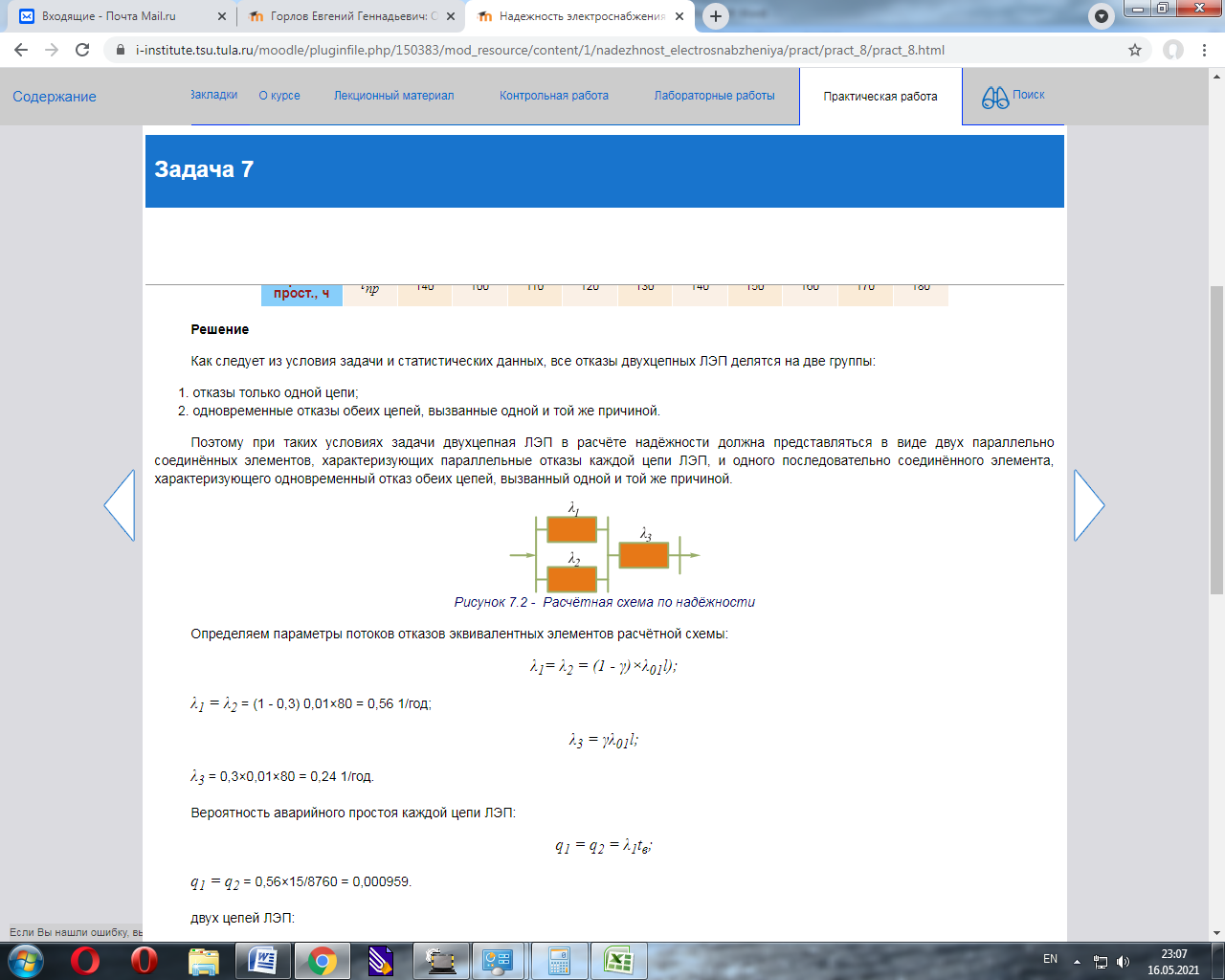



Рисунок 7.2 -  Расчётная схема по надёжности

Определяем параметры потоков отказов эквивалентных элементов расчётной схемы:

λ₁= λ₂ = (1 - γ)×λ₀₁l);

λ₁ = λ₂ = (1 - 0,3)*0,045*130 = 4,095 1/год;

λ₃ = γλ₀₁l;

λ₃ = 0,3*0,045*130 = 1,755 1/год.

Вероятность аварийного простоя каждой цепи ЛЭП:

q₁ = q₂ = λ₁t_в;

q₁ = q₂ = 4,095*40/8760 = 0,0187.

двух цепей ЛЭП:

q₃ = λ₃t_в2;

q₃ = 1,755*140/8760 = 0,0028.

Вероятность простоя каждой цепи в преднамеренном отключении:

q_п = t_пр/Т ;

q_п = 160/8760 = 0,0183.

Параметр потока отказов двухцепной ЛЭП:

λ_∑ = λ₃ + 2λ₁(q₁ + q_п);

λ_∑ = 1,755 + 2*4,095*(0,0187 + 0,0183) = 2,06 1/год.

Здесь q₁ + q₂ - вероятность аварийного и преднамеренного отключения одной цепи.

Вероятность простоя двухцепной ЛЭП:

q_∑ = q₁q₂ + 2Кq₁q_п + q₃.

В этом выражении неизвестной величиной является коэффициент, учитывающий уменьшение вероятности совпадения аварийных и плановых ремонтов одной цепи вследствие того, что возможно лишь наложение аварийного ремонта на плановый, а не наоборот.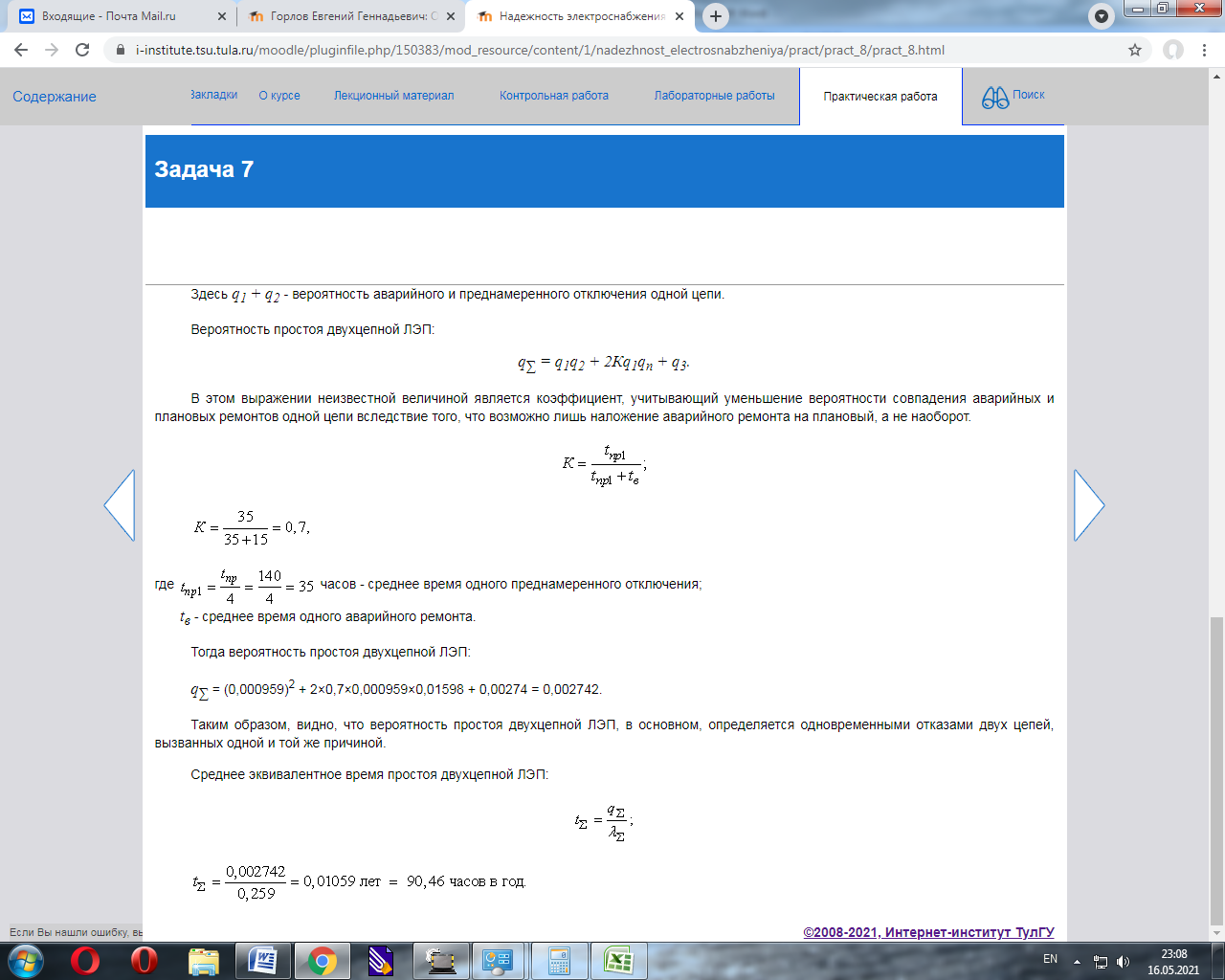



K=40/(40+40)=0,5

где t_пр1=160/4=40  часов - среднее время одного преднамеренного отключения;

t_в - среднее время одного аварийного ремонта.

Тогда вероятность простоя двухцепной ЛЭП:

q_∑ = (0,0187)^2 + 2*0,5*0,0187*0,0183 + 0,0028 = 0,0035.

Таким образом, видно, что вероятность простоя двухцепной ЛЭП, в основном, определяется одновременными отказами двух цепей, вызванных одной и той же причиной.

Среднее эквивалентное время простоя двухцепной ЛЭП: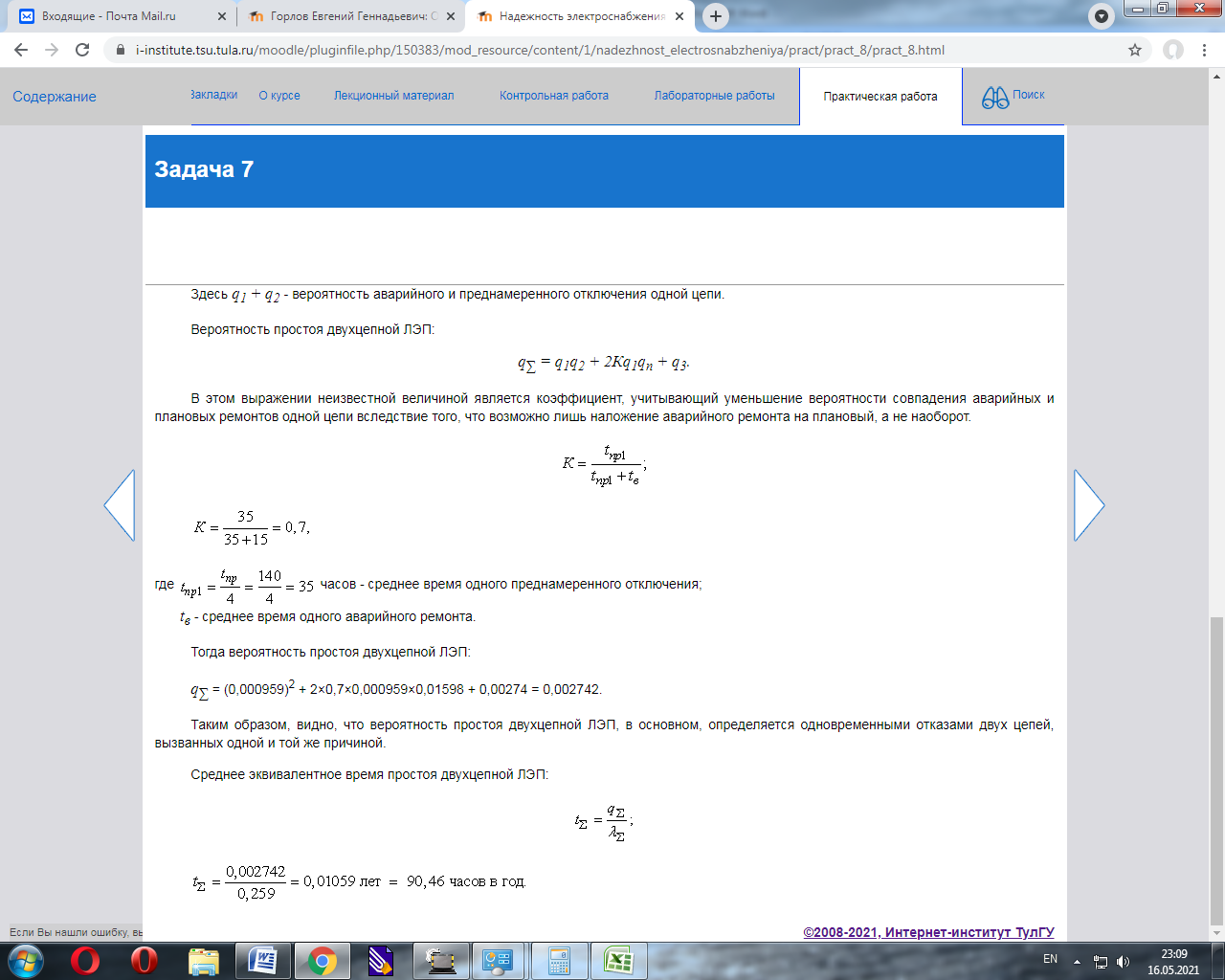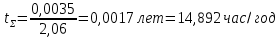

Задача 8

Две одноцепных линии электропередачи напряжением 110 кВ, длиной l, км, сооружённые на разных опорах, имеют следующие показатели надёжности: среднее значение параметра потока отказов одной цепи λ₀₁, 1/км·год, второй цепи λ₀₂, 1/км·год. Доля отказов линии, приводящих к отключению двух цепей по одной причине равна γ. Среднее время аварийного восстановления каждой цепи t_в, час. Время планового простоя одной цепи t_пр, час/год при четырех отключениях в год. Пропускная способность каждой цепи - 100% передаваемой мощности.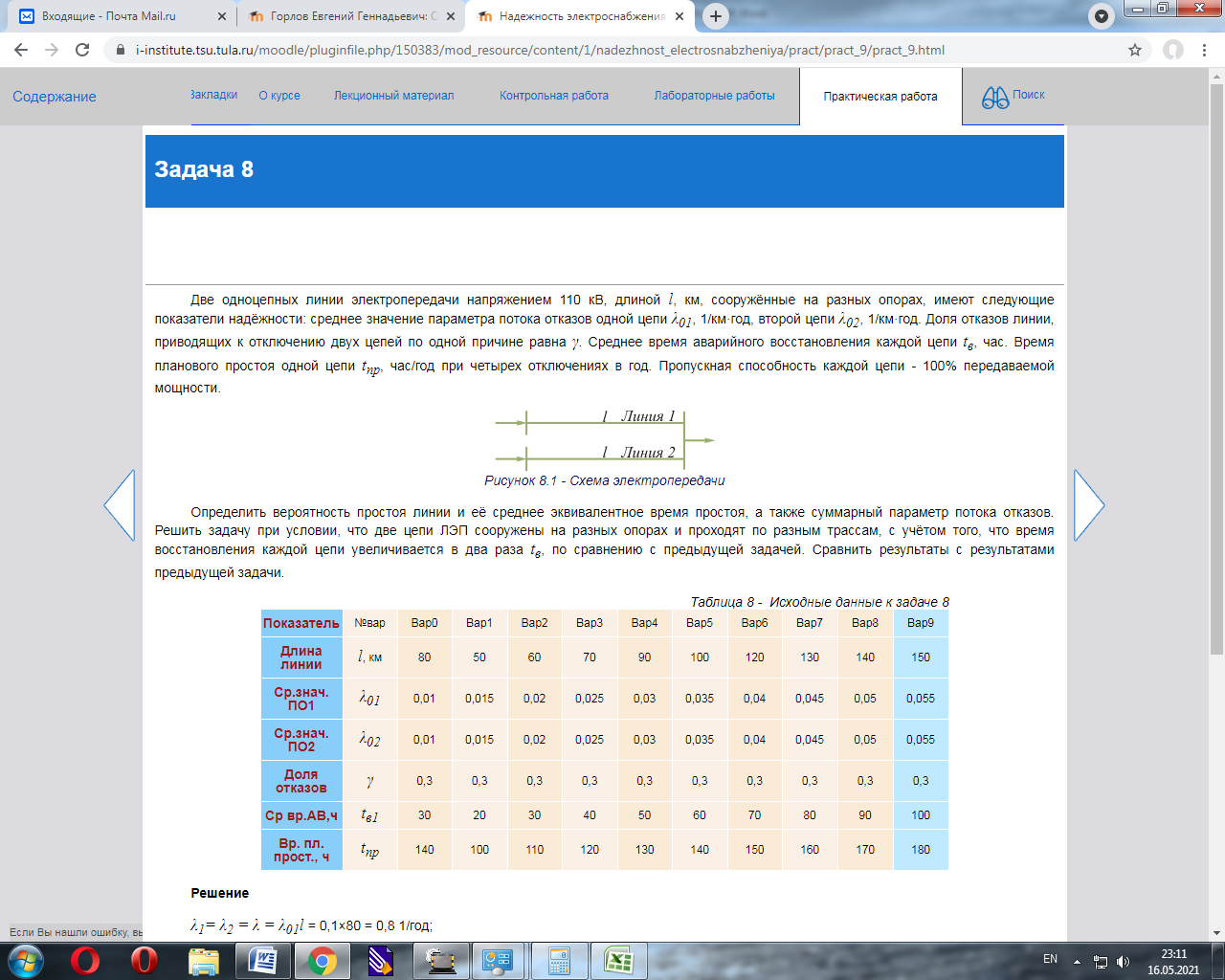



Рисунок 8.1 - Схема электропередачи

Определить вероятность простоя линии и её среднее эквивалентное время простоя, а также суммарный параметр потока отказов. Решить задачу при условии, что две цепи ЛЭП сооружены на разных опорах и проходят по разным трассам, с учётом того, что время восстановления каждой цепи увеличивается в два раза t_в, по сравнению с предыдущей задачей. Сравнить результаты с результатами предыдущей задачи.

Таблица 8 -  Исходные данные к задаче 8
Показатель	№вар	Вар7
Длина линии	l, км	130
Ср.знач. ПО1	λ01	0,045
Ср.знач. ПО2	λ02	0,045
Доля отказов	γ	0,3
Ср вр.АВ,ч	tв1	80
Вр. пл. прост., ч	tпр	160

Решение

λ₁= λ₂ = λ = λ₀₁l = 0,045×130 = 5,85 1/год;

q₁ = q₂ = 5,85*80/8760  = 0,00534;

q_п = t_пр/Т;

q_п = 160/8760 = 0,0183.

λ_S = 2λ₁(q₁ + q_п);

λ_S = 2*5,85*(0,00534+0,0183) = 0,2765 1/год;

q_∑ = q₁² + 2Кq₁q_п;

q_∑ = 0,00534^2  + 2*(40/(40+80))*0,00534*0,0183 = 9,366*10^-5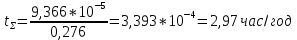

;



Сравнивая полученный результат с результатом предыдущей задачи, видим, что эквивалентное время простоя двух одноцепных линий уменьшилось в 14,892/2,97 = 5,01 раз. Примерно во столько же раз, можно считать, уменьшается недоотпуск электроэнергии.

Список литературы

1. 
   Балабанов В.Н. Надежность электроустановок: Учебно-методическое пособие. – Хабаровск: ДВГУПС, 1999, - 97с.
   
2. 
   Ефимов А.В., Галкин А.Г. Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж/д транспорта. – М.: УМК МПС России, 2000 – 512с.
   
3. 
   Анищенко В.А. Надежность систем электроснабжения: Учебное пособие. Мн.: УП «Технопринт», 2001. – 160с.