практическая по менеджменту. практические задачи. Практическая работа по дисциплине Производственный менеджмент Выполнил студент гр. Проверил ст преподаватель Тюмень, 2022 Задача
 Скачать 233.71 Kb. Скачать 233.71 Kb.
|
|
1/3 продукции отправляется на склад (стратегия A2), 2/3 продукции дополнительно обрабатывается (стратегия A3), при этом цена игры 8,67. Задача Фирма, занимающаяся перевозкой грузов на собственных автомобилях КамАЗ, обслуживает своих клиентов в центральных городах России. Клиенты могут заказать фирме доставку груза из любого населенного пункта в любой город. После доставки КамАЗы ждут распоряжений диспетчера о выполнении следующей заявки в том городе, куда был доставлен груз. В настоящий момент 4 порожних автомобиля ждут распоряжений диспетчера в Иваново, 3 автомобиля – в Костроме, 6 машин – в Орле и одна – в Калуге. Одновременно диспетчеру поступили заявки на 5 автомобилей во Владимире, на 3 автомобиля в Санкт-Петербурге и на 6 автомобилей в Москве. Расстояния между городами известны и приведены в таблице.
Требуется: составить такой план перегона порожних автомобилей из мест их расположения к клиентам, чтобы суммарный пробег всех автомобилей, а следовательно, и издержки фирмы были минимальными; Выяснить, как изменится оптимальный план, если стало известно, что в Калуге освободилась еще одна машина, а в Москве появился дополнительный заказчик. РЕШЕНИЕ: Обозначим через xij количество машин, направляемых из i-го города к j-му клиенту. Тогда искомый план перевозок будет содержать 12 неизвестных
Математически задача формулируется следующим образом. Необходимо сформировать такой план ( xij ), при котором целевая функция Z - суммарный порожний пробег транспортных средств, будет минимальным. Z = 119 х11 + 971 х12 + 287 х13 + 214 х21 + 1008 х22 + 324 х23 +………+135 х43 На искомые переменные наложены ограничения: • По свободным машинам, ожидающим распоряжений: х11 + х12 + х13 = 4, х21 + х22 + х23 = 3, х31 + х32 + х33 = 6, (7.17) х41 + х42 + х43 = 1. • По заявкам клиентов: х11 + х21 + х31 + х41 = 5, х12 + х22 + х32 + х42 = 3, х13 + х23 + х33 + х43 = 6. Кроме того, переменные неотрицательны: xij >= 0 (i=l, 2, 3, 4; j =1, 2, 3). Данная задача относится к классической замкнутой транспортной задаче линейного программирования. Решаем задачу в MS Excel 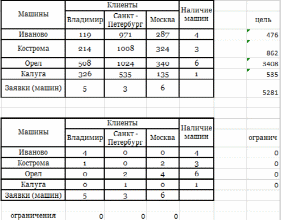 Ответ: Оптимальный план перегона автомобилей к заказчикам, следующий: · во Владимир направляются 4 машины из Иваново и одна из Костромы; · в С.-Петербург – 2 машины из Орла и одна из Калуги; · в Москву – 2 машины из Костромы и 4 из Орла. При этом будет обеспечен наименьший суммарный пробег всех автомашин, который составит 5281 км. Если дополнительно в Калуге освободится еще одна машина, а в Москве появится еще один заказчик, то оптимальный план изменится. В этом случае во Владимир направляются 4 машины из Иваново и одна — из Костромы. 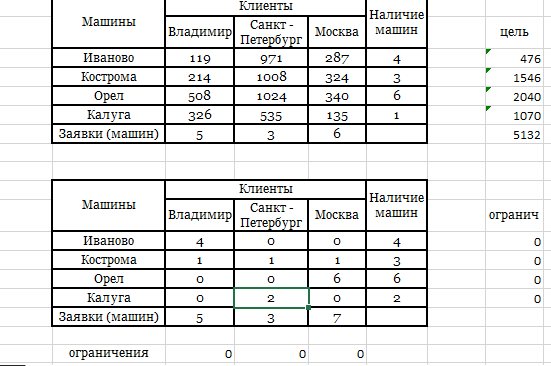 Задача Заменить колесо машины (работу выполняют два человека). Достать из багажника домкрат и инструменты (40 с); снять диск с колеса (30 с); освободить колесо (50 с); поставить домкрат под машину (20 с); из багажника взять запасное колесо (25 с); снять гайки и колесо (20 с); установить запасное колесо на ось (10 с); завинтить (не сильно) гайки на оси (15 с); опустить машину и собрать домкрат (25 с); поставит домкрат обратно в багажник (10 с); завинтить гайки на оси до конца (12 с); поставить на место диск колеса (10 с). Составить сеть работ. РЕШЕНИЕ: Сетевой график. Все работы выполняются последовательно двумя людьми. 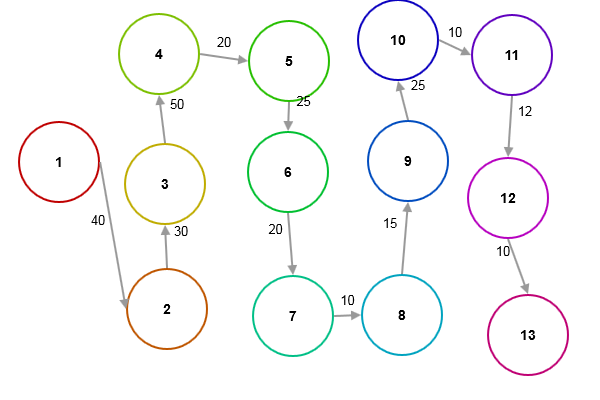 Продолжительность критического пути: 267 с или 4,45 мин. Задача Компания производит ГСМ. За прошлые годы спрос составил 5, 7, 8 или 9 тонн. Расчет вероятности привел к значениям 0,1, 0,2, 0,5 и 0,2 соответственно. Затраты на производство 1 тонны равны 43 д.ед., компания продает каждую тонну за 64 д.ед. Непроданный в течение года объем резко ухудшает свои свойства и подлежит уничтожению. Сколько тонн ГСМ должна производить фирма, если исходить из критерия максимизации прибыли с учетом риска? (построить дерево решений + расчет) Решение: Выполним вспомогательные расчеты
Для выпуска 5 тн затраты составят 5 * 43 = 215 Выручка 5 * 64 = 320 Аналогично по другим вариантам. Составим платежную матрицу. Значения в этой таблице представляют собой размер прибыли, который получит компания при различных сочетаниях выпуска и спроса.
Проще всего заполняется первая строка в этой таблице, т.к. при выпуске 5 тн весь произведенный объем будет продан со 100% -ой вероятностью независимо от состояния спроса. 320 – 215 = 105 В случае, если принимается решение выпускать 7 тн, расчет выполняется следующим образом. При спросе 5 тн из предыдущей таблицы берем размер выручки от реализации 5 тн и вычитаем из нее размер затрат на выпуск 7 тн. При спросе 7 тн из предыдущей таблицы берем размер выручки от реализации 7 тн и вычитаем из нее размер затрат на выпуск 7 тн. При спросе 8 тн из предыдущей таблицы берем размер выручки от реализации 7 тн (мы не можем продать больше, чем произвели) и вычитаем из нее размер затрат на выпуск 7 тн. Аналогично заполняем значения прибыли для других сочетаний выпуска и спроса. Средняя ожидаемая прибыль для каждого выпуска рассчитывается суммированием произведений прибыли на вероятность того или иного спроса. Например, при выпуске 7 тн 19*0,1 + 147*0,2 + 147*0,5 + 147*0,2 = 134,2 Максимум прибыли достигается в случае принятия решения о выпуске 8 тн. Именно столько тонн ГСМ должна производить кампания.  Прибыль 105 с вероятностью 100%  5 тн                            Прибыль 189 с вероятностью 20% Прибыль 125 с вероятностью 50% Прибыль 61 с вероятностью 20% Прибыль -67 с вероятностью 10% Прибыль 168 с вероятностью 70% Прибыль 104 с вероятностью 20% Прибыль -24 с вероятностью 10% Прибыль 147 с вероятностью 90% Прибыль 19 с вероятностью 10% 9 тн 8 тн 7 тн Выбор объема | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
