практическая по менеджменту. практические задачи. Практическая работа по дисциплине Производственный менеджмент Выполнил студент гр. Проверил ст преподаватель Тюмень, 2022 Задача
 Скачать 233.71 Kb. Скачать 233.71 Kb.
|
|
Этап II. Улучшение опорного плана. Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0. u1 + v1 = 7; 0 + v1 = 7; v1 = 7 u3 + v1 = 3; 7 + u3 = 3; u3 = -4 u3 + v4 = 6; -4 + v4 = 6; v4 = 10 u1 + v2 = 13; 0 + v2 = 13; v2 = 13 u4 + v2 = 0; 13 + u4 = 0; u4 = -13 На данном этапе возникла ситуация, когда для оставшихся занятых клеток не известно ни одного из потенциалов. Это результат вырожденности решения. Для его преодоления в одну из клеток нужно внести нулевую поставку, таким образом, такая клетка станет условно занятой. Для неизвестного потенциала u2 нулевую поставку можно разместить в клетках: (2;1), v1=7 (2;2), v2=13 (2;4), v4=10 Для неизвестного потенциала v3 нулевую поставку можно разместить в клетках: (1;3), u1=0 (3;3), u3=-4 (4;3), u4=-13 Среди этих клеток, в которых может быть размещена нулевая поставка, наименьший тариф имеет клетка (4, 3) с c43 = 0. Следовательно, нулевую поставку размещаем в клетку (4, 3), и она становится условно занятой. u4 + v3 = 0; -13 + v3 = 0; v3 = 13 Ранее поставленный псевдоноль из ячейки (1;1) убираем. u2 + v3 = 7; 13 + u2 = 7; u2 = -6
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj> cij (1;3): 0 + 13> 9; ∆13 = 0 + 13 - 9 = 4> 0 Выбираем максимальную оценку свободной клетки (1;3): 9 Для этого в перспективную клетку (1;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
Цикл приведен в таблице (1,3 → 1,2 → 4,2 → 4,3). Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (4, 3) = 0. Прибавляем 0 к объемам грузов, стоящих в плюсовых клетках, и вычитаем 0 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0. u1 + v2 = 13; 0 + v2 = 13; v2 = 13 u4 + v2 = 0; 13 + u4 = 0; u4 = -13 u1 + v3 = 9; 0 + v3 = 9; v3 = 9 u2 + v3 = 7; 9 + u2 = 7; u2 = -2 u1 + v4 = 8; 0 + v4 = 8; v4 = 8 u3 + v4 = 6; 8 + u3 = 6; u3 = -2 u3 + v1 = 3; -2 + v1 = 3; v1 = 5
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj> cij (2;2): -2 + 13> 8; ∆22 = -2 + 13 - 8 = 3> 0 Выбираем максимальную оценку свободной клетки (2;2): 8 Для этого в перспективную клетку (2;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
Цикл приведен в таблице (2,2 → 2,3 → 1,3 → 1,2). Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 40. Прибавляем 40 к объемам грузов, стоящих в плюсовых клетках, и вычитаем 40 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0. u1 + v2 = 13; 0 + v2 = 13; v2 = 13 u2 + v2 = 8; 13 + u2 = 8; u2 = -5 u4 + v2 = 0; 13 + u4 = 0; u4 = -13 u1 + v3 = 9; 0 + v3 = 9; v3 = 9 u1 + v4 = 8; 0 + v4 = 8; v4 = 8 u3 + v4 = 6; 8 + u3 = 6; u3 = -2 u3 + v1 = 3; -2 + v1 = 3; v1 = 5
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vj ≤ cij. Минимальные затраты составят: F(x) = 13*90 + 9*40 + 8*110 + 8*40 + 3*90 + 6*20 + 0*60 = 3120 Из 1-го склада необходимо груз направить к 2-у потребителю (90 ед.), к 3-у потребителю (40 ед.), к 4-у потребителю (110 ед.) Из 2-го склада необходимо весь груз направить к 2-у потребителю. Из 3-го склада необходимо груз направить к 1-у потребителю (90 ед.), к 4-у потребителю (20 ед.) Потребность 2-го потребителя остается неудовлетворенной на 60 ед. 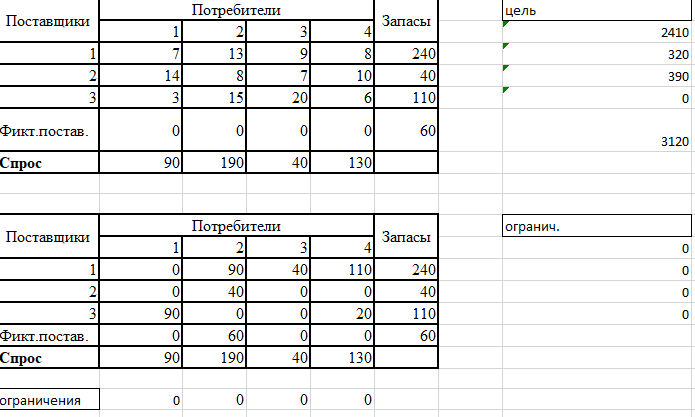 Задача Предприятие выпускает скоропортящуюся продукцию, которую может сразу отправить потребителю - стратегия А1, отправить на склад для хранения – А2, подвергать дополнительной обработке для длительного хранения – А3. Потребитель может приобрести продукцию немедленно – В1, в течение небольшого времени – В2, после длительного периода времени – В3. В случае стратегии А2 и А3 предприятие несет дополнительные потери на хранение и обработку продукции, которая не требуется для А1. Однако при А2 следует учесть возможность убытка из-за порчи продукции, если потребитель выбирает стратегию В2, В3. Определить оптимальные пропорции продукции для применения стратегии А1, А2, А3, при следующей матрице затрат.
РЕШЕНИЕ: Получаем игру с платежной матрицей
В этой матрице первую строку можно отбросить как невыгодную (ее элементы меньше соответствующих элементов второй строки). Матрица примет вид.
Элементы первого столбца больше соответствующих элементов второго столбца, поэтому его можно отбросить. Игра упростилась
Мы свели игру 3 x 3 к игре 2 x 2.
Находим решение P2 = 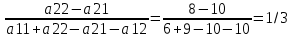 P3 =  Цена игры, y = 26/3 = 8,67 Оптимальная стратегия производителя продукции: стратегия A1 не применяется, |
