конспект. Практическая работа по информатике в 11 классе Решение задачи оптимального планирования

• Название: Практическая работа по информатике в 11 классе Решение задачи оптимального планирования
• Анкор: конспект
• Дата: 27.04.2023
• Размер: 158.5 Kb.
• Имя файла: rprakt_rabota_po_informatike_v_11_klasse_reshenie_zadachi_optima.doc
• Тип: Практическая работа; #1094905

МБОУ «Учхозская средняя общеобразовательная школа» Краснослободского муниципального района Республики Мордовия

Практическая работа по информатике в 11 классе

«Решение задачи оптимального планирования»

Урок подготовил и провел: учитель информатики и ИКТ Бахарев Юрий Владимирович
п. Преображенский -2021

Цель урока: научить учащихся решать задачи оптимального планирования средствами MS Excel.

Задачи:

1. 
   познакомить учащихся с особым видом экономических задач – задач оптимального планирования, способом их решения в среде MS Excel;
   
2. 
   закрепить навыки работы с формулами в среде электронных таблиц;
   
3. 
   развивать умение анализировать и обобщать материал, строить математическую модель задачи;
   
4. 
   воспитывать самостоятельность и ответственность в принятии решения.
   

Оборудование:

1. 
   Компьютер преподавателя
   
2. 
   Компьютеры учащихся – 10 шт.
   
3. 
   Локальная сеть
   
4. 
   Программное обеспечение: MS PowerPoint, MS Excel
   

Продолжительность урока: 40 мин.

 

Ход урока

1. 
   Организующее начало урока.
   
2. 
   Выявление имеющихся знаний и умений.
   

1. а) Что такое корреляционная зависимость?

б) Что такое корреляционный анализ?

в) Какие типы задач можно решать с помощью корреляционного анализа?

г) Какая величина является количественной мерой корреляции? Какие значения она может принимать?

2. 
   С помощью какого средства табличного процессора можно вычислить коэффициент корреляции?
   
3. 
   а) Для данных из таблицы, представленной на рис. 2.18, постройте две линейные регрессионные модели.
   

б) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.

4. Практическая работа 3.6 «Решение задачи оптимального планированияl»

Цели работы:

• получение представления о построении оптимального плана методом линейного программирования;

• практическое освоение раздела MS Excel «Поиск решения» для построения оптимального плана.

Используемое программное обеспечение: табличный процессор Microsofxt Excel.
Задание1.

Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («зерно и картофель»), как воспользоваться указанным средством.

Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х₁ га(площадь отведенная для посевов зерна ) и х₂га(площадь отведенная под картофель). Ниже этих ячеек представлена система неравенств (а), определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция (Р) занесена в ячейку В15.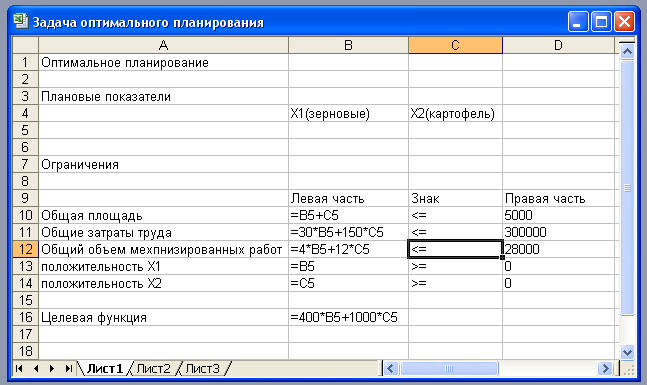
Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду => Сервис => Поиск решения. На экране откроется соответствующая форма (рис. 2)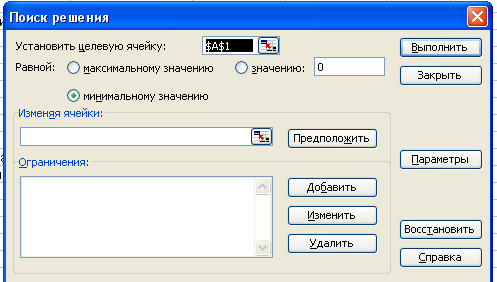


Далее надо выполнить следующий алгоритм:

1. 
   Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).
   
2. 
   Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.
   
3. 
   В поле «Изменяя ячейки» ввести В5:С5, то есть сообщить, какое место отведено под значения переменных -плановых показателей.
   
4. 
   В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10<=D10; B1K=D11; B12>=D12; B13>=D13. Ограничения вводятся следующим образом:
   

=> щелкнуть по кнопке «Добавить»;

в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11<=D11 и так далее. В конце надо щелкнуть на кнопке ОК.

5. Закрыть диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения» (рис. 3).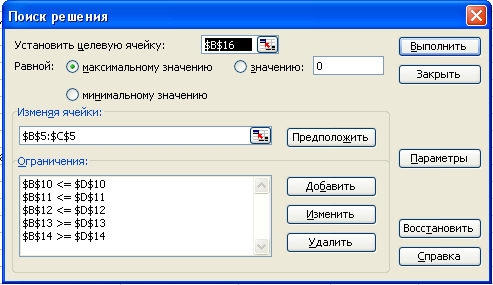


6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры» — появится форма «Параметры поиска решения» (рис. 4).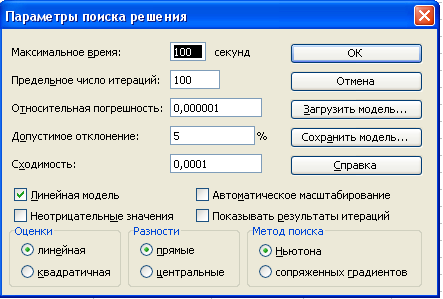

7. 
   Надо выставить флажок на переключателе «Линейная модель» Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения».
   

Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 4000 и 1000), а также число 2600000 в ячейке В16 — максимальное значение целевой функции (рис. 5).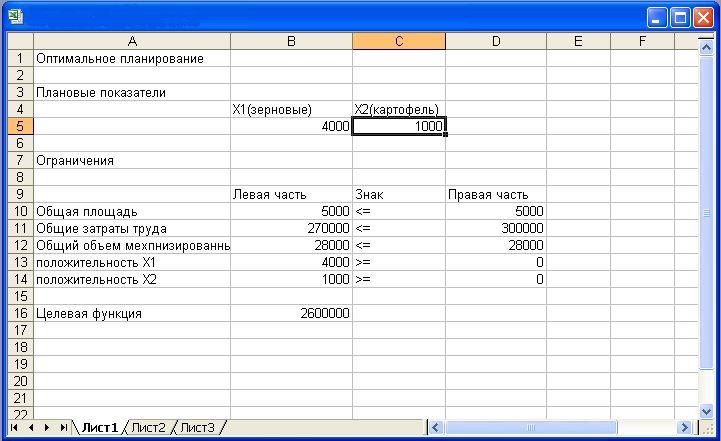


Этап III. Оптимальное сочетание посевных площадей культур: зерновые — 4000 га, картофель—1000 га. Существенно провести экономический анализ оптимального решения задачи.

При х₁=4000 и х₂=1000 х₁ + х₂=5000, а это значит, что пашня используется полностью.

4 х₁ + 12 х₂≤ 300 000= 4·4000+ 12·1000 = 28 000. Это означает, что ресурсы тракторного парка используются полностью.

30 х₁ + 150 х₂= 30·4000+150·1000 = 270 000. Мы выяснили, что трудовые ресурсы недоиспользованы на 30 000 чел.·ч. Полное использование трудовых ресурсов сдерживается ограниченностью пашни и мощностью тракторного парка. Как видим, для рассмотренного в задаче совхоза ресурсы имеют разную ценность: человеческих рук в избытке, а механизированный труд дефицитен.

5. Закрепление новой темы по вопросам:

1. 
   В чем состоит задача оптимального планирования?
   
2. 
   Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.
   
3. 
   Попробуйте сформулировать содержание оптимального планирования своей учебной деятельности.
   
4. 
   Что такое математическое программирование, линейное программирование?
   

6. Д/З § 20, читать конспект, составить математическую модель для решения 1 задачи

Список используемой литературы:

1. Семакин И.Г Учебник Информатика и ИКТ. Базовый уровень 11 класс.. М. Бином 2019г.

2. И.М. Шапиро. Использование задач с практическим содержанием в преподавании математики. М. Просвещение 1990 г.