Построение сетевых графиков и работа с ними. Практическая работа. Практическая работа Построение сетевых графиков и работа с ними Цель работы
 Скачать 0.84 Mb.
|
|
Практическая работа Построение сетевых графиков и работа с ними Цель работы: Изучить основные понятия сетевого моделирования и теории графов. Научиться находить оптимальное решение той или производственной или коммерческой ситуации. Уметь строить графики заданного комплекса работ, рассчитывать временные характеристики сетевого графика при нормальном режиме работ; находить критический путь, полные резервы времени, временные характеристики сетевого графика при срочном режиме работ, критический путь, полные резервы времени, стоимость работ. В результате освоения учебной дисциплины обучающийся должен уметь: использовать и рассчитывать показатели и критерии оценивания информационной системы, осуществлять необходимые измерения. В результате освоения учебной дисциплины обучающийся должен знать: реинжиниринг бизнес-процессов; модели жизненного цикла информационной системы, методы проектирования информационной системы; оценку необходимых ресурсов для реализации проекта. Теоретическая часть Поиск более эффективных способов планирования сложных процессов привели к необходимости использования моделей сетевого планирования и управления (СПУ). СПУ основано на моделировании процесса с помощью сетевого графика (сетевой модели). Сетевая модель представляет план выполнения некоторого комплекса работ. Главными элементами сетевого графика является событие и работа. Событие – это завершение, какого либо процесса, отражающий отдельный этап выполнения проекта. На сетевом графике событие изображается кружком. Работа – процесс, связанный с затратами времени и ресурсов и приводящий к получению определённых результатов. Работами считают также процессы, не требующие расходов ресурса, а только времени. Действительная работа — протяжённый во времени процесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т. п.). Зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами (событиями), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю. 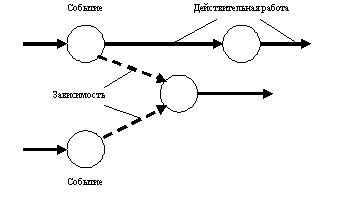 Рис. 1 Основные элементы сетевой модели  При составлении сетевых графиков (моделей) используют условные обозначения. События на сетевом графике изображаются кружками (вершинами графа), а работы — стрелками (ориентированными дугами):— событие,  — работа (процесс), — фиктивная работа — применяется для упрощения сетевых графиков (продолжительность всегда равна 0).Среди событий сетевой модели выделяют исходное и завершающее события. Исходное событие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий. Сетевой график «работы–связи» в отличие от графика «события–работы» обладает известными преимуществами: не содержит фиктивных работ, имеет более простую технику построения и перестройки, включает только хорошо знакомое исполнителям понятие работы без менее привычного понятия события. Если в сетевой модели нет числовых оценок, то такая сеть называется структурной. Известны два метода сетевого планирования: CPM – метод критического пути при фиксированном числе работ для составления расписания, и PERT – метод оценки и пересмотра программ. Правила построения классических сетевых графиков Для правильного отображения взаимосвязи между работами сетевого графика при его построении необходимо соблюдать ряд правил. Первое правило. Если работы А, Б и В выполняются последовательно, то на сетевом графике изображаются по горизонтали одна за другой (рисунок 2). 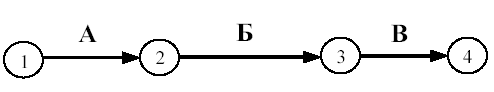 Рис. 2. Первое правило Второе правило. Если результат работы А необходим для выполнения работ Б и В, то на сетевом графике это отображается следующим образом (рисунок 3). 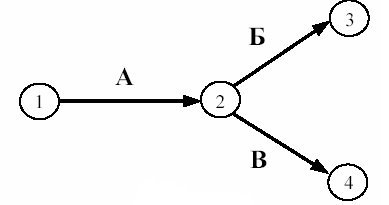 Рис.3. Второе правило Третье правило. Если результат работ Г и Д необходим для выполнение работы Е, то на сетевом графике это изображается так (рисунок 4). 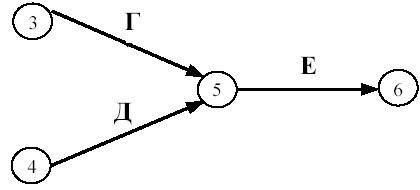 Рис. 4. Третье правило Четвертое правило. Работы сетевого графика не должны иметь одинакового кода. Если работы Б, В, Г выходят из одного события и выполнение необходимо для свершения одного и того же события, то вводятся дополнительные фиктивные работы (рисунок 5). 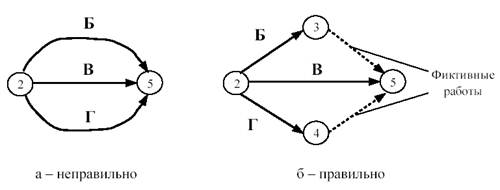 Рис. 5. Четвертое правило Пятое правило. Если работы Б, В и Г начинаются после частичного выполнения работы А, то работа А разбивается на части А1, А2 ... Аi и т.д., при этом каждая работа А в сетевом графике считается самостоятельной работой (рисунок 6). 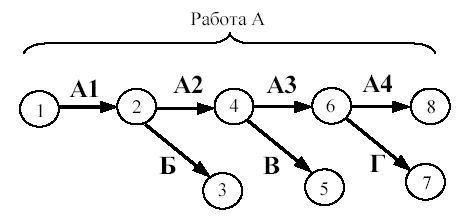 Рис. 6. Пятое правило Шестое правило. Если для начала работы Ж необходимо выполнение работ В и Г, а для начала работы Д выполнение работы Г, то в сетевой график вводится дополнительная фиктивная работа (рисунок 7). 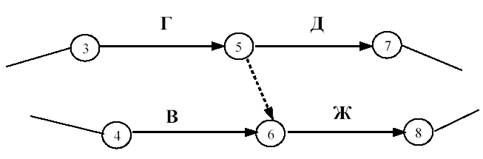 Рис. 7. Шестое правило Седьмое правило. Если после окончания работы А можно начать работу Б, а после окончания работы В работу Г, а работа Д может быть начата только после окончания работ А и В, то на сетевом графике это изображается с помощью двух дополнительных фиктивных работ (рисунок 8). 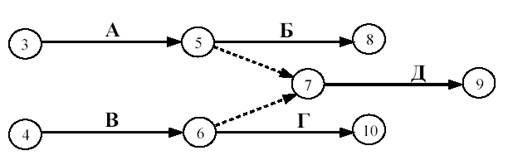 Рис. 8. Седьмое правило Восьмое правило. В сетевом графике не должно быть замкнутых контуров (циклов), т.е. цепочек работ, возвращающихся к тому событию, из которого они вышли. На рисунке 9 замкнутый контур (цикл) образовался из событий 3, 4, 2, 3. Наличие цикла в сети свидетельствует об ошибке в исходных данных или в неправильном изображении взаимосвязи работ (рисунок 9). 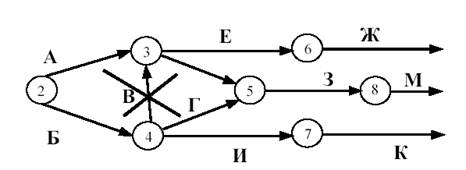 Рис. 9. Восьмое правило Девятое правило. События следует кодировать так, чтобы номер начального события данной работы был меньше номера конечного события этой работы (рисунок 10). 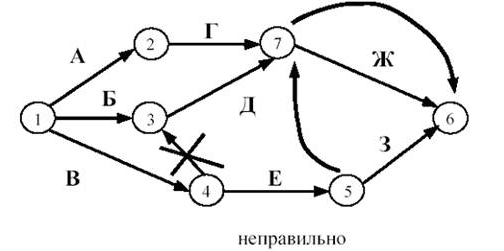 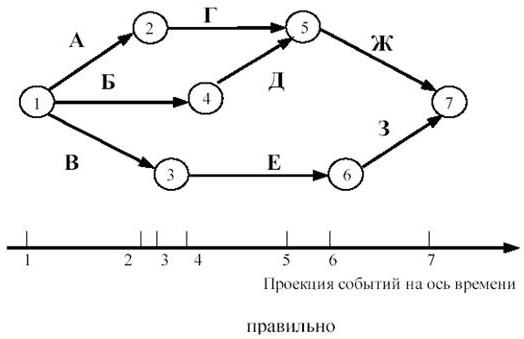 Рис.10. Девятое правило Десятое правило. В одноцелевом сетевом графике не должно быть "тупиков", т.е. таких событий, из которых не выходит ни одной работы. (рисунок 11). 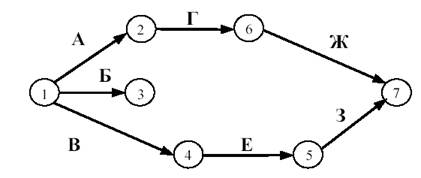 Рис. 11. Десятое правило Одиннадцатое правило. В сетевом графике не должно быть "хвостов", т.е. событий, в которые не входит ни одной работы, если эти события не являются исходными для данного сетевого графика. 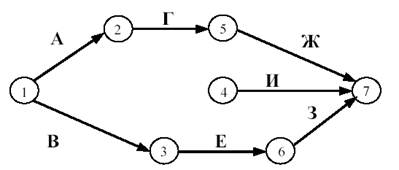 Рис. 12. Одиннадцатое правило Двенадцатое правило. При укрупнении сетевых графиков группа работ может изображаться как одна работа, если в этой группе имеется одно конечное событие и если эти работы выполняются одним исполнителем при наличии в группе входных и выходных работ. Понятие о пути Одно из важнейших понятий сетевого графика — понятие пути. Путь — любая последовательность работ, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы. Среди различных путей сетевого графика наибольший интерес представляет полный путь— любой путь, начало которого совпадает с исходным событием сети, а конец — с завершающим. Наиболее продолжительный полный путь в сетевом графике называется критическим. Критическими называются также работы и события, находящиеся на этом пути. Условия критичности пути необходимое условие: нулевые резервы событий, лежащих на критическом пути  ;достаточное условие: нулевые полные резервы работ, лежащих на критическом пути  .  — показывает максимальное время, на которое можно увеличить длительность работы (i,j) или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом.Временные параметры сетевых графиков Ранний (или ожидаемый) срок свершения события определяется продолжительностью максимального пути, предшествующего этому событию. Поздний (или предельный) срок свершения события равен разности максимального времени наступления последующего за работой события и времени работы до этого (будущего) события. Резерв времени события определяется как разность между поздним и ранним сроками его свершения. Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ. Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события. Отдельная работа может начаться (и окончиться) в ранние, поздние или другие промежуточные сроки. В дальнейшем при оптимизации графика, возможно, любое размещение работы в заданном интервале, называемом продолжительностью работы. Очевидно, что ранний срок начала работы совпадает с ранним сроком наступления предшествующего события. Ранний срок окончания работы совпадает с ранним сроком свершения последующего события. Поздний срок начала работы совпадает с поздним сроком наступления предшествующего события. Поздний срок окончания работы совпадает с поздним сроком наступления последующего события. Если путь не критический, то он имеет резерв времени, определяемый как разность между длиной критического пути и рассматриваемого. Он показывает, на сколько в сумме могут быть увеличены продолжительности всех работ, принадлежащих этому пути. Среди резервов времени работ выделяют четыре разновидности: Полный резерв времени работы показывает, на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв времени работы равен резерву максимального из путей, проходящего через данную работу. Частный резерв времени первого вида есть часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока её начального события. Частный резерв времени второго вида, или свободный резерв времени работы представляет часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока её конечного события. Независимый резерв времени работы — часть полного резерва времени, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки. Работы, лежащие на критическим пути, так же как и критические события, резервов времени не имеют. Практическая часть Часть 1. Расчет временных параметров Основным временным параметром сетевого графика является продолжительность критического пути. Расчет критического пути состоит из двух этапов. Можно выделить: Прямой подход. Вычисление начинают с исходного события и продолжают до тех пор, пока не будет достигнуто завершающее событие. Для каждого события вычисляется одно число, соответствующее раннему сроку наступления этого события; Обратный подход. Вычисления начинают с завершающего события и продолжают, пока не будет достигнуто исходное событие. Для каждого события вычисляется поздний срок его наступления. Рассмотрим прямой подход. Введем обозначения:  - ранний срок начала всех работ, следующих за событием i;  - ранний срок начала всех работ, предшествующих событию j;  - продолжительность работы (i,j);  ;  - ранний срок окончания работы;  - поздний срок окончания всех работ, предшествующих событию i;  - поздний срок начала работ; n – завершающее событие сети;  для всех (i,j). Пример 1 Для заданной сетевой модели некоторого комплекса работ определить время, критический путь и оптимальный путь, ранние сроки начала и окончания работ, поздние сроки начала и окончания работ, резервы времени.
На основе данных таблицы построим сетевой график создания прибора с учетом изложенных рекомендаций.  Г=2.          А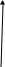=2.  Ж=2   Б=3. В=3 И=6 Д=3  Е=7 З=5К=2  Для данного графа выпишем частичные и полные пути, определим критический путь и оптимальный. Частичные пути: L1= (0, 1); L2= (0, 1, 3); L3= (0, 1, 3, 5); L4= (0, 2); L5= (0, 2, 3); L6= (0, 2, 3, 5); L7= (0, 2, 4); L8= (0, 2, 4,5). Полные пути: L1= (0, 1, 3, 6); L2= (0, 1, 3, 5, 6); L3= (0, 2, 3, 6); L4= (0, 2, 3, 5, 6); L5= (0, 2, 4, 5, 6); L6 = (0, 2, 4, 6). Определим ранние сроки начала всех работ из предыдущего примера. Для исходного события ранний срок начала работ равен позднему сроку окончания работ и равен нулю tpн(0) = tпо(0) = 0 где tpн(0) – ранний срок начала работ исходного события; tпо(0) – поздний срок окончания исходного события. Ранний срок начала работ tpн(j) совершения j-го события определяется по формуле tpн(j) = tpн(i) + Т(i-j) где Т(i-j) – продолжительность работы, ч; tpн(i) – ранний срок начала предшествующего события, ч. Если событие имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то для оценки раннего срока совершения j-го события следует выбирать максимальный из предшествующих путей.  ;  ;  ;  ;  ;  . Найдем ранние сроки окончания работ. Этот срок является наиболее ранним (минимальным) из возможных моментов окончания работы при заданной продолжительности работ, т.е.  . Поэтому           Рассчитаем обратный проход. Если i=n, то  и является отправной точкой обратного прохода. Т.о.  для всех работ (i,j)и поэтому  ;  ;  ;  ;  ;   Вычислим поздние сроки начала работ. Эти сроки являются наиболее поздними (максимальными) из допустимых моментов начала данной работы, при которых еще возможно выполнение всех последующих работ в установленный срок, т.е.  . Следовательно:           Существует три вида резерва времени: полный резерв (  ), независимый резерв (rн) и свободный резерв  . Независимый резерв времени работ найдем по формуле rн(i,j)=tрнj –tпоi – tij Полный резерв показывает, на сколько может быть увеличена сумма продолжительности всех работ относительно критического пути, представляет разность между максимальным отрезком времени, в течение которого может быть выполнена работа, и его продолжительность рассчитывается по формуле  . Результаты вычислений:           Свободный резерв времени – максимальное время, на которое можно отсрочить начало или увеличить продолжительность работы, при условии, что все события наступают в ранние сроки:  . вычислим свободные резервы для всех работ:          Следует отметить, что критические работы имеют нулевой полный резерв времени, при этом свободный резерв также должен быть равен нулю. Используя результаты вычислений при прямом и обратном проходах, можно определить работы критического пути. Работа (i,j)принадлежит критическому пути. Если для нее выполняются условия  ,  ,  . В рассматриваемом примере критический путь включает в себя работы (0,2), (2,4), (4,5), (5,6) с общим временем выполнения работ 18 недель. Все расчеты запишем в таблицу.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||