пз_4 -1. Практическая работа Принципы установления законов распределения случайной величины

Название	Практическая работа Принципы установления законов распределения случайной величины
Дата	28.02.2022
Размер	120.42 Kb.
Формат файла
Имя файла	пз_4 -1.docx
Тип	Практическая работа #377583
страница	1 из 7

1 2 3 4 5 6 7

_{Практическая работа}_{«Принципы установления законов распределения случайной величины»}
Цель: научить студентов устанавливать законы распределения показателей надежности по статистическим данным
Пример

На основе представленных статистических данных провести расчет и анализ показателей надежности серии невосстанавливаемых объектов.

Исходные данные:

Таблица 1 – Данные об отказах оборудования

№ объекта	Время наблюдения	Время отказа, час	Число отказов
1	1150	155, 291, 340, 396, 900, 1145	6
2	1990	90, 180, 460, 853, 1761, 1987	6
3	3020	420, 930, 1213, 1916, 2005, 2774, 3015	7
4	3600	300, 830, 1430, 1933, 2247, 2968, 3220, 3561	8
5	2250	301, 610, 1700, 1900, 2100, 2250	6
6	3000	68, 415, 888, 1231, 1717, 1917, 2090, 2967	8
7	2898	87, 211, 715, 1600, 1903, 2115, 2344, 2898	8
8	2050	60, 280, 395, 470, 850, 1050, 2000	7
9	1350	50, 158, 484, 945, 1120, 1300	6
10	2550	81, 240, 793, 1145, 1781, 1973, 2005, 2500	8

Решение.

Получение простого статистического ряда

Определяем наработку до отказа по всем объектам. Для этого из каждого последующего времени возникновения отказа вычитаем предыдущее. Для удобства расчетов данные представляем в виде таблицы.

Таблица 2 – Нахождение значений наработки на отказ

№ изделия	Т1	Т2	Т3	Т4	Т5	Т6	Т7	Т8
1	2	3	4	5	6	7	8	9
1	155	136	49	56	504	245
2	90	90	280	393	908	226
3	420	510	283	703	89	769	241
4	300	530	600	503	314	721	252	341
5	301	309	1090	200	200	150
6	68	347	473	343	486	200	173	877
7	87	124	504	885	303	212	229	554
1	2	3	4	5	6	7	8	9
8	60	220	115	75	380	200	950
9	50	108	326	461	175	180
10	81	159	553	352	636	192	32	495

Выстраиваем полученные данные в порядке возрастания. Находим максимальное и минимальное значение из полученного простого статистического ряда.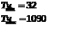

Определяем диапазон значений или амплитуду статического ряда.

Обработка статистического ряда

Количество данных равно 70. Определяем количество интервалов.

.

Определяем длину интервала

.

Рассчитываем частость и накопленную частость по всем интервалам. Данные сводим в таблицу 3.

Таблица 3 – Расчет частости и накопленной частоты

No интервала	Начало интервала в час.	Конец интервала в час.	Кол-во изд. отказав. в интервале, Δni(Δti)	Частость, Δn(Δt)/N	Накопленная частость, Σ(Δn(Δt)/N)
1	30	170	19	0,27	0,27
2	170	310	21	0,30	0,57
3	310	450	9	0,13	0,70
4	450	590	11	0,16	0,86
5	590	730	4	0,06	0,91
6	730	870	1	0,01	0,93
7	870	1010	4	0,06	0,99
8	1010	1150	1	0,01	1,00
			Σ=70	Σ=1,00

Строим гистограммы по полученным значениям частости и накопленной частости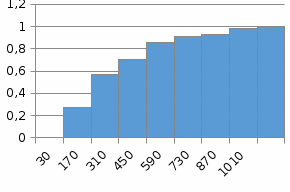

Рисунок 1 – Гистограмма частости Рисунок 2 – Гистограмма накопленной частости

Расчет показателей безотказности по статистическим данным

Определяем количество работоспособных изделий на середину каждого периода по формуле

Определяем статистическую оценку вероятности безотказной работы на середину каждого периода по формуле

.

Определяем количество отказавших деталей нарастающим итогом на середину каждого периода по формуле

Определяем статистическую оценку вероятности отказа на середину каждого периода по формуле

.

Определяем статистическую оценку плотности вероятности отказов по формуле

.

Результаты расчета для удобства сводим в таблицу 4

Таблица 4. – Расчет показателей безотказности по экспериментальным данным

Начало интервала	Конец интервала	Середина интервала	Количество отказавших изделий в интервале	Количество отказавших изделий на середину интервала	Количество работоспособных изделий на середину интервала	R(t)	Q(t)	f(t)
1	2	3	4	5	6	7	8	9
30	170	100	19	9,5	60,5	0,86	0,14	0,00097
170	310	240	21	29,5	40,5	0,58	0,42	0,00301
310	450	380	9	44,5	25,5	0,36	0,64	0,00454
1	2	3	4	5	6	7	8	9
450	590	520	11	54,5	15,5	0,22	0,78	0,00556
590	730	660	4	62	8	0,11	0,89	0,00633
730	870	800	1	64,5	5,5	0,08	0,92	0,00658
870	1010	940	4	67	3	0,04	0,96	0,00684
1010	1150	1080	1	69,5	0,5	0,01	0,99	0,00709

Строим график зависимости вероятности безотказной работы R(t) и вероятности отказа Q(t) по экспериментальным данным.

Рисунок 3 – График зависимости вероятности безотказной работы и вероятности отказа от времени.

Расчет числовых характеристик наработки до отказа.

Средняя наработка до отказа определяется по формуле:

,

где n_i – количество отказов изделий в рассматриваемом интервале; t_i_сер – середина рассматриваемого интервала.

Таблица 5 – Промежуточные расчеты средней наработки до отказа

Середина интервала	Кол-во изд. отказав. в интервале	tc*ni	tc^2*ni
100	19	1900	190000
240	21	5040	1209600
380	9	3420	1299600
520	11	5720	2974400
660	4	2640	1742400
800	1	800	640000
940	4	3760	3534400
1080	1	1080	1166400
		Σ=24360	Σ=12756800

Дисперсия: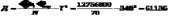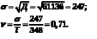

Выбор закона распределения и его параметры.

Выдвигаем гипотезу по закону распределения средней наработки до отказа. Если ν>0,5, то данная случайная величина подчиняется закону Вейбулла. В данном случае 0,71>0,5, следовательно, выбираем закон распределения Вейбулла).

Основная гипотеза Н0 – средняя наработка до отказа подчинена закону Вейбулла.

Основная гипотеза Н1 – средняя наработка до отказа не подчинена закону Вейбулла.

Определяем характеристики закона распределения Вейбулла: коэффициент формы и масштаба. Воспользуемся номограммой на рисунке 4.

Рисунок 4 – Номограмма для определения параметра закона Вейбулла

По рисунку 4 определяем параметр α для соответствующего значения ν, при ν=0,71 будет α=1,47.

Рассчитаем параметр λ: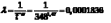

Простая гипотеза Н0– средняя наработка до отказа подчиняется закону Вейбулла с параметрами: α=1,47; λ=0,0001836.

Подтверждение гипотезы

Для подтверждения гипотезы используем критерий согласия Пирсона (χ²), который характеризует отклонение теоретической кривой от практической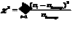

;

При расчете необходимо объединить интервалы с количество данным менее 5.

Расчет ведем для 5-ти интервалов:

.

Результаты расчета представляем в таблице 6.
Таблица 6.

Начало интервала	Конец интервала	Середина интервала	Кол-во изд. отказав. в интервале	Pit	nit	ni-nit	(ni-nit)^2	(ni-nit)^2/nit
30	170	100	19	0,294	20,61	-1,61	2,61	0,13
170	310	240	21	0,275	19,28	1,72	2,97	0,15
310	450	380	9	0,198	13,84	-4,84	23,41	1,69
450	590	520	11	0,119	8,30	2,70	7,29	0,88
590	730	660	4	0,063	4,38	-0,38	0,15	0,03
730	870	800	1	0,030	2,09	-1,09	1,19	0,57
870	1010	940	4	0,013	0,91	3,09	9,53	10,43
1010	1150	1080	1	0,005	0,37	0,63	0,40	1,07
				Σ=0,997				Σ=χ²=14,95

χ² расчетное равно 14,95. Сравним χ² расчетное с χ² теоретическим: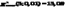

,

14,95<15,09 , следовательно, т.к. χ² расчетное < χ² теор. – гипотеза верна, отклонения меньше допустимых, т.е. наработка до отказа подчиняется закону Вейбулла с такими параметрами.

Расчет показателей безотказности по теоретическим данным.

ti	f(t)	R(t)	Q(t)
0	0	1	0
30	0,0012990	0,973	0,027
170	0,0021281	0,706	0,294
310	0,0017208	0,430	0,570
450	0,0011079	0,232	0,768
590	0,0006164	0,114	0,886
730	0,0003065	0,051	0,949
870	0,0001389	0,021	0,979
1010	0,0000580	0,008	0,992
1150	0,0000225	0,003	0,997

Рисунок 5 – График теоретической зависимости вероятности безотказной работы и вероятности отказа от времени

Рисунок 6 – График теоретической зависимости плотности распределения отказов во времени

1 2 3 4 5 6 7