Теория вероятностей и математическа статистика Жаукенова А.Е. Практическая работа. Задание Буквы, составляющие слово ракета, написаны по одной на шести
 Скачать 25.57 Kb. Скачать 25.57 Kb.
|
|
Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» Кафедра менеджмента Форма обучения: заочная с применением ДОТ
МОСКВА 2021 Практическая работа. Задание 1. Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет. 1.1. Чему равна вероятность того, что, вынимая четыре буквы, получим слово РЕКА? Решение: Найдем вероятность выбора первой буквы Р: Количество событий = общему количеству букв = 6. Из них благоприятных событий (подходящих букв) = 1. Вероятность по формуле Лапласа: Р = 1/6. Вероятность, что вторая буква Е: Р = 1/5 (из остав.5ти букв 1 Е); Вероятность того, что третья буква будет К: Р = 1/4 (из остав.4х букв 1 К); Вероятность того, что четвертая буква будет А: Р=2/3(из остав.3х букв 2А); Вероятность взаимосвязанных событий. Что поочередно вынуты буквы Р, Е, К, А: Р=(1/6)*(1/5)*(1/4)*(2/3)=1/180 Ответ: Вероятность того, что, вынимая четыре буквы, получим слово РЕКА равна 1/180. 1.2.Какова вероятность сложить слово КАРЕТА при вынимании всех букв? Решение: Найдем вероятность выбора первой буквы К: Количество событий = общему количеству букв = 6. Из них благоприятных событий (подходящих букв) = 1. Вероятность по формуле Лапласа: К = 1/6. Вероятность, что вторая бука А: Р = 2/5(из оставшихся 5ти букв 2 А); Вероятность того, что третья буква будет Р: Р = 1/4 (из остав.4х букв 1 Р); Вероятность того, что четвертая буква будет Е: Р = 1/3(из остав.3х букв 1 Е); Вероятность того, что пятая буква будет Т: Р = 1/2 (из остав.2х букв 1 Т); Вероятность того, что шестая буква будет А: Р = 1/1 (из остав.1х букв 1 А); Вероятность взаимосвязанных событий, что поочередно вынуты буквы К, А, Р, Е, Т, А: Р = (1/6)*(2/5)*(1/4)*(1/3)*(1/2)*(1/1) = 1/360 Ответ: Вероятность того, что, при вынимании всех букв, получим слово КАРЕТА равна 1/360. Задание 2. Дискретная случайная величина ξ задана следующим законом распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. Решение: Математическое ожидание находим по формуле 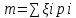 Математическое ожидание 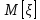 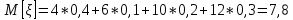 Дисперсию находим по формуле 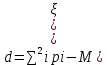 Дисперсия 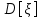 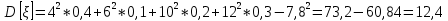 Среднее квадратическое отклонение 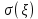 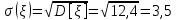 Задание 3. Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание 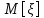 = 1.9, а также = 1.9, а также 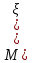 = 7.3, найти вероятности = 7.3, найти вероятности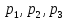 которые соответствуют дискретным значениям случайной величины. которые соответствуют дискретным значениям случайной величины.Решение: Дисперсия случайной величины ξ: 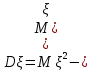 , поскольку ξ дискретная, то , поскольку ξ дискретная, то 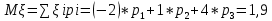 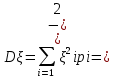 Учитываем условие, что 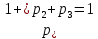 Решаем как систему уравнений: 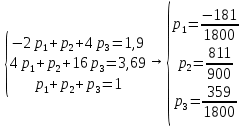 Значение вероятности 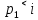 0, что наверно, поэтому задача не имеет решения. 0, что наверно, поэтому задача не имеет решения.Ответ: Так как значение вероятности 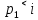 0, задача не имеет решения. 0, задача не имеет решения. | |||||||||||||||||||
