Конструкционная безопасность. Глава 3 определ подкрановой балки. Практические приложения

• Название: Практические приложения
• Анкор: Конструкционная безопасность
• Дата: 07.06.2022
• Размер: 270.05 Kb.
• Имя файла: Глава 3 определ подкрановой балки.docx
• Тип: Документы; #574658
• страница: 4 из 5

ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ДЕФОРМИРОВАНИЮ И РАЗРУШЕНИЮ ПРИ МАЛОЦИКЛОВОМ НАГРУЖЕНИИ

(Лабораторная работа)
Цель работы.

Экспериментальное определение параметров обобщенных диаграмм статического и циклического деформирования и характеристик сопротив- ления разрушению.
Постановка задачи.

Испытание при малоцикловом нагружении является основным ме- тодом определения сопротивления деформированию и разрушению в условиях однородных напряженных состояний.
При экспериментальном нагружении наиболее нагруженных эле- ментов нефтегазохимических объектов в зонах концентрации напряжений сварных швов, локальных контактных взаимодействий и дефектов возни- кают статические и циклические упругопластические деформации.

В связи с этим, в дополнение к общепринятым стандартным испы- таниям при однократном растяжении осуществляются испытания лабора- торных образцов при малоцикловом упругопластическом нагружении. Эти испытания предусмотрены как одни из видов испытаний на усталость в широком диапазоне нагрузок и долговечностей. Основной целью предла- гаемых испытаний является экспериментальное определение важных ха- рактеристик деформирования и разрушения, позволяющих обоснованно выбирать конструкционные материалы для заданных условий нагружения и проводить расчетную оценку деформативности, прочности и долговечности при статическом и малоцикловом нагружении (см. часть I).

Эти испытания могут проводится как на лабораторных образцах из основного металла, так и на образцах со сварным швом.

Основным режимом нагружения при лабораторных испытаниях яв- ляется режим мягкого нагружения – нагружения с заданными амплитудами

нагрузок Р_а (напряжений

_а ). При этом

  ^Ра

а _F

(1)

Возникающие при этом деформации зависят от свойств материала и числа циклов нагружения

_а , механических

Схема нагружения цилиндрического образца с рабочей длиной  ₀ и

 _d² 

d₀ ^ F₀ ^{0 } показана на рис. 1.

 ⁴ 

l₀
Р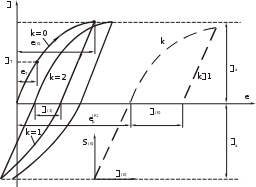




Рис. 1
Обычно реализуются близкие к синусоидальным циклам циклы из- менения нагрузок Р или напряжений  по уравнению 1 в зависимости от времени нагружения . В силу малости деформаций деформаций можно принять F=F₀.

При таком режиме нагружения деформации после достижения пре-

дела текучести _т

становятся упругопластическими и достигают величин

_e(0)

при

_a  ⁽⁰⁾ . Исходный полуцикл k=0 деформирования определяет

сопротивление статическим деформациям в условиях изменения напряже-

ний от 0 до

⁽⁰⁾ . После достижения этого напряжения осуществляется

разгрузка до =0 и последующее нагружение в области сжатия до уровня

напряжений

_a . От точки разгрузки в области растяжения до достижения

напряжений _a

в области сжатия реализуется первый полуцикл нагруже-

ния (k=1). В дальнейшем производится следующее нагружение в область

растяжения до уровня напряжений _a

цикл нагружения k=2).

(то есть реализуется второй полу-

Полуциклы k=1 и k=2 на оси деформаций е определяют ширину

петли упругопластического деформирования

⁽¹⁾ . При дальнейшем накоп-

лении числа циклов до k и k+1 регистрируется ширина петли

_(К)

и сле-

дующие петли

_е(к) _.

р
Если в точке начала k-полуцикла поместить начало координат

«S^(K)  ^(K) » то, получим диаграмму циклического деформирования в этих координатах. Для каждого из последующих полуциклов k+1, k+2, и т.д. получаются свои диаграммы деформирования в координатах «S-». Это

означает, что для данного материала при данной амплитуде напряжений _a

и данном числе полуциклов нагружения получается своя диаграмма цик- лического деформирования « S^(K)  ^(K) ». Указанные обстоятельства прак- тически исключают возможность проведения испытаний при всех воз-

можных режимах нагружения (при варьировании _a

и k).

Использование общеизвестной диаграммы циклического деформи- рования позволяет записать связь между напряжениями «S-» для любых

_a и k. Как везде в I части, параметры обобщенных диаграмм деформиро-

вания и являются целью проведения лабораторных испытаний.

Если циклическое нагружение продолжить до разрушения, то можно

определить долговечность N для заданного значения

_a . Испытывая серию

образцов (8-10), можно построить кривую усталости « _a -N» (рис. 2).

a в a a K K I II III 1 N

Рис. 2

На кривой усталости N=1 (однократное нагружение) откладываются

величины

_a = _в

( _в

• 
  предел прочности материала при статическом рас-
  

тяжении и _К

• 
  сужение образца в шейке
  

К
  ^{F0  FK} 100% F₀
(2)

где

d²

F_K - площадь образца в шейке при разрушении ( F_K ^K , d_K – диа-

4

метр образца в шейке).

Область I по числу циклов N, когда сохраняется постоянным значение

_К (на уровне _К

при статическом однократном разрушении) называется

областью квазистатических малоцикловых разрушений).

По мере снижения _К ( _К  0) разрушения носят усталостный ха-

рактер (зона III). Им предшествует образование в рабочей части образца трещин усталости (как при классической малоцикловой усталости). Между областями квазистатических разрушений (зона I) и усталостных разруше- ний (зона III) располагается зона переходных разрушений (зона II). В по- следней зоне наблюдается образование не выраженной шейки с трещинами в шейке.

Описанные выше испытания проводятся на механических или гид- равлических машинах с предельными усилиями до 100 кН, при этом раз- меры образцов составляют d₀=510 мм,  ₀ =2550 мм.

Порядок проведения опыта

1. 
   Измерить размеры поперечного сечения образца d₀,  ₀ .
   
2. 
   Установить образец в захватах машины.
   
3. 
   Установить на образце деформометр для измерения продольных
   

деформаций е на базе

 ₀ .

4. 
   Включить системы измерения усилий Р и деформаций е (через двухкоординатные самописцы или компьютер).
   
5. 
   Установить на шкале нагрузок предельные нагрузки Р, соответ-
   

ствующие амплитудам напряжений _a

в полуциклах растяжения и сжатия.

6. 
   Включить режим нагружения в нулевом полуцикле (k=0) и заре- гистрировать диаграмму исходного нагружения до точки ( ⁽⁰⁾  е⁽⁰⁾ ).
   
7. 
   Продолжить циклическое нагружение с регистрацией диаграмм
   

деформирования в полуциклах k (обычно выбирают ряд k = 0, 1, 2, 3, 5, 7,

10, 20, 30, 50, 70, 100 и т.д.).

8. 
   Довести образец до разрушения при циклическом нагружении с регистрацией последнего цикла N.
   
9. 
   После разрушения образца зарегистрировать d_K в зоне разрушения.
   

Обработка результатов опыта.

1. 
   По результатам записи диаграмм деформирования, провести раз- метку измеряемых параметров нагружения и деформирования в соответ- ствии с рисунками 1 и 2.
   

2. 
   Установить амплитуду напряжений _a
   

по формуле 1.

3. 
   Определить предел текучести _т
   

формаций к пластическим).

(точка перехода от упругих де-

4. 
   Определить модуль продольной упругости
   

Е  _т е_т .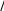

5. 
   Определить коэффициент упрочнения в упругопластической об- ласти из соотношения
   

_{ е}(0) _^m

lg⁽⁰⁾  

т

т
⁽⁰⁾   ^{ }

 ^ет 

m  lg e⁽⁰⁾ e 

(3)

6. 
   Построить зависимость ширины петли
   

_(К)

от числа полуциклов k

и установить характер циклического поведения материала:

• 
  если с ростом k величина ^(К)
  

чески разупрочняющимся;

растет, то материал является цикли-

• 
  если с ростом k величина ^(К) уменьшается, то материал является циклически упрочняющимся;
  

• 
  если с ростом k величина ^(К)
  

практически не изменяется, то ма-

териал является циклически стабильным.

6. 
   По построенным функциям
   

^(К)  F(k)

(4)

определяются параметры  и  циклического деформирования соответ- ственно для материалов указанных в п. 6.

^(К)  ⁽¹⁾ exp(k 1)

_(К) _{ }(1)_k

_(К) _{ }(1)
(5)

8. 
   По уравнениям (6) определяются параметры С и В
   

  С(е⁽⁰⁾  е_т )

  В(⁽⁰⁾  _т )

(6)

9. По зависимости


т
⁽¹⁾  Ае⁽⁰⁾  е 

(7)

определяется параметр А.
10. Величины _т, Е, _в, _к, А, В, С заносятся в протокол испытаний.

По параметрам В и С устанавливается принадлежность материала к циклически упрочняющемуся или разупрочняющемуся. Если В=С=0, то материал принимается циклически стабильным.