Конструкционная безопасность. Глава 3 определ подкрановой балки. Практические приложения

• Название: Практические приложения
• Анкор: Конструкционная безопасность
• Дата: 07.06.2022
• Размер: 270.05 Kb.
• Имя файла: Глава 3 определ подкрановой балки.docx
• Тип: Документы; #574658
• страница: 5 из 5

ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ РАЗРУШЕНИЯ K_Iс ПРИ НАЛИЧИИ ДЕФЕКТА ТИПА ТРЕЩИНЫ

(Лабораторная работа)
Цель работы.

Определение критического значения коэффициента интенсивности напряжений K_Iс (вязкость разрушения) при статическом изгибе образца с трещиной (острым надрезом).
Постановка задачи.

Испытание на вязкость разрушения является одним из основных ме- тодов определения сопротивления металлов разрушению при наличии ис- ходных дефектов типа трещин в условиях статического нагружения (изги- ба).

Так как в реальных изделиях практически трудно исключить воз- можность образования дефектов на стадии их изготовления или эксплуа- тации (расслой, заковы, горячие и холодные трещины от сварки, непровары, усталостные или коррозионные трещины), то на ряду со стандартными испытаниями лабораторных образцов без макродефектов в последние годы предложен ряд методов определения характеристик прочности при наличии дефектов. Основной целью предлагаемых испытаний является экспери- ментальное определение таких характеристик разрушения, которые бы позволяли более обоснованно выбирать материал с учетом его трещино- стойкости, а также проводить расчетную проверку прочности элемента конструкции с дефектами или устанавливать предельно допустимые раз- меры дефекта при заданных условиях эксплуатации. Выбор таких харак- теристик базируется на анализе напряженного и деформированного со- стояния в вершине трещин. При этом трещины можно рассматривать как надрезы, имеющие бесконечно малые радиусы закругления в вершине.

Если пластину из упругого (хрупкого) материала большой ширины В, имеющую боковой надрез глубиной  с радиусом закругления в вер- шине  растягивать при номинальных напряжениях , то в минимальном сечении пластины напряжения будут распределены (фиг.1) неравномерно, т.е. будут зависеть от  и Х.

_y  f , X

На контуре надреза

_y  _max , при

x  ,

(1)
_y   . Максимальное

напряжение на контуре определяется по известной формуле

^max

 _ , (2)

где

_ – теоретический коэффициент концентрации напряжений.

Величина
_  1 К

_ для рассматриваемой пластины зависит от  и 
, (3)

где К – коэффициент (К1).

При

  0

или

  

величина

_  l и

_max  

т.е. при отсут-

ствии концентрации имеет место равномерное распределение напряжений. Если при заданной глубине надреза  уменьшать радиус  (   0 ), то

величина _ по уравнению (3) будет увеличиваться ( _   ); макси-

мальные напряжения на контуре

^max

по (2) также будут повышаться

^{( }max

  ), и будет усиливаться неравномерность распределения напря-

жений (фиг2).

у  y max  х  В 	у max  3  y 1 2 2 1 х х 3
Фиг. 1	Фиг. 2

Решение задачи теории упругости для трещины (   0 ), полученное

Д.Ирвином показало, что напряжения _у

непосредственно у вершины

трещины (при Х < 0,1  ) распределены по закону

К
_у 
(4)

где Х – расстояние от вершины трещины до рассматриваемой точки; К – коэффициент.

При Х0 (т.е. у вершины трещины) напряжения _у

по уравнению (4)

увеличиваются ( _у   ), что следует из проведенного выше анализа концентрации напряжений.

Распределение напряжений _у

по Х, описываемое уравнением (4) , не

зависит от формы пластины и способа ее нагружения (растяжение, изгиб).

Таким образом, абсолютные значения напряжений _у

в рассматриваемой

точке будут определяться величиной К; следовательно, величина К характеризует интенсивность распределения напряжений у вершины трещины. Велична К называется коэффициентом интенсивности напряжений.

Для пластины из упругого материала деформации _у

на основе

закона Гука будут пропорциональны

_у , тогда по (4)

  ^у

у <sub>Е

</sub>К Е
(5)

Если проинтегрировать дефомации е_у на участке   Х  0 , то на

основе (5) можно получить перемещения v_y в направлении у, которые определяют раскрытие трещины или форму ее берегов (фиг. 3).

берега трещины 2vy =0 2v =0 0

Фиг. 3

Это интегрирование дает

v_y  К

(6)

В пластине из упругого материала при Х0, v_y0, т.е. берега трещины стыкуются плавно. При Х=  , v_y=v.

Так как напряжения _у у вершины трещины (для 0) на основе (1),

3. 
   и (4) зависят только от  и  , то и величина К зависит от  и  .
   

Решение указанных выше задач теории упругости дает К  а

где а – коэффициент, зависящий от отношения  /В.

(7)

Если пластину из упругого материала нагружать при возрастающих нагрузках, Р, соответствующих напряжениям  , то при достижении кри- тического состояния произойдет разрушение пластины. Номинальные напряжения  , соответствующие моменту разрушения, называются кри-

тическими

_с . Если эти напряжения подставить в уравнение (7), то можно

получить критическое значение коэффициента интенсивности напряжении К_Ic, т.е.

К_с  а_с

(8)

Распределение напряжений по Х в минимальном сечении описыва- ется уравнением (4) при K = K_c, а распределение перемещений - уравнением (6).

При известных величинах

К_с и _с

на основе (8) можно определять

предельный размер трещины  в конструкции, а при известных К_с и 

можно определять предельные напряжения _с .

Из сказанного следует, что для экспериментального определения

критического значения коэффициента интенсивности напряжений

К_с для

образца с трещиной из упругого материала необходимо измерить началь- ную длину трещины  , установить по справочным данным коэффициент а и установить из опыта для момента разрушения критическое номинальное

напряжение

_с .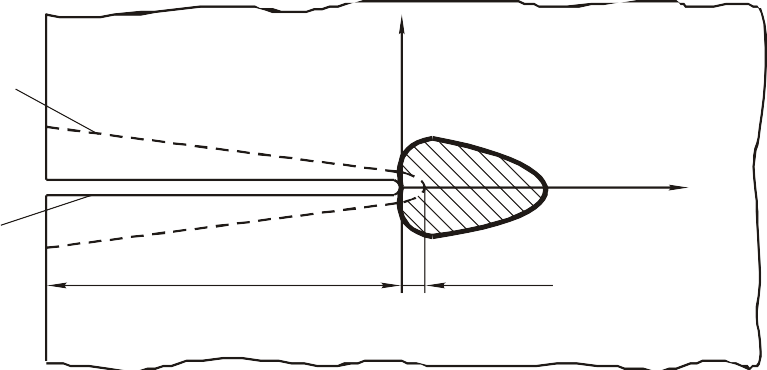

По величинам  , а и _с

па основе (8) рассчитывается величина

К_с .

у  =0 х l l

Фиг. 4

Если пластина с трещиной изготовлена не из упругого, а из упру-

го-пластичного материала, то при увеличении напряжений в вершине трещины возникнут зоны пластических деформаций, трещина удлинится на

величину ; за счет пластических деформаций и роста трещины переме-

щения v_y при Х=0 будут отличны от нуля (эти перемещения обозначаются


X0
через ; т.е.   2v_y  ).

При достижении напряжениями критической величины _с

величины

 , v и  принимают значения _с , v_с и _с. В связи с перераспределением

напряжений в пластических зонах разрушающие напряжения _с _в

упруго-пластичного (вязкого) материала оказываются выше, чем _с _Х

для для

упругого (идеально хрупкого) материала. Зависимости  , v и  для вязкого материала на фиг. 5 показаны сплошными линиями, для идеально хрупкого материала - пунктирными. Графические зависимости между  и  назы- ваются диаграммами разрушения.

Если понизить (за счет снижения температуры испытаний, увеличе- ния скорости нагружения и степени объемности напряженного состояния в вершине трещины) способность вязкого материала к образованию пласти- ческих деформаций у вершины трещины, то характер разрушения вязкого материала будет мало отличаться от характера разрушения хрупкого ма-

териала, _с _в _с _Х . В этих условиях для исходного вязкого материала

получаются минимальные критические значения коэффициентов интен- сивности напряжений, обозначаемых через К_Ic (где индекс I - означает разрушение нормальным отрывом в плоскости начальной трещины).

На фиг. 6 показаны зависимости K-v (или   v, или P  v ) для не-

большого образца (линия 1) и более крупного образца (линия 2), имеющего пониженную пластичность в зоне разрушения.

 (C)в (C)x  v l 0 l l, , v	К 3  Р H K PIc с Ic К P с Ic 2 1   v
Фиг. 5	Фиг. 6

Опыты показывают, что величину K_Ic (как одну из основных харак- теристик сопротивления хрупкому разрушению) можно приближенно определить по результатам испытаний небольшого образца, если на диа-

грамме K-v (линия 1) провести прямую линию 3 под углом '  до пере-

сечения с линией 1 ( tg'  0,95tg ). Таким образом, для определения ве- личины K_Ic для данного материала и температуры испытания надо провести опыт с нагружением образца имеющего начальный острый дефект типа трещины. В этом опыте должны быть зарегистрированы усилия Р и пере-

мещения v берегов трещины. При этом, если разрушение носит хрупкий характер (т.е. отклонение зависимости Р-v от линейной мало), то по вели- чине Р_Iс в момент разрушения можно определить _с и по формуле (8)

рассчитать К_с  К_Ic . Если разрушение не является хрупким (выраженная

нелинейность зависимости

P  v ), то расчет

^КIc

производится по условной

нагрузке

P'_Ic , соответствующей точке пересечения линии 3, идущей под

углом

' , с линией 1 на фиг 6.

Испытание на изгиб плоского образца с трещиной проводится на

механической машине Р-5 с предельным усилием 5 тонн; усилия Р и пере- мещения берегов трещины v регистрируются автоматически на двухкоор- динатном самописце ПДС-021.
Порядок проведения опыта.

1. 
   Измерить размеры поперечного сечения образца 1 в ненадрезанной части (В и h), глубину (  ) начального острого надреза типа трещины и расстояние между опорами L (фиг.7).
   
2. 
   Установить на образце опорные устройства 3 и датчик 4 для изме- рения перемещений v (фиг. 7).
   
3. 
   Установить образец на опоры машины.
   
4. 
   Подвести вручную упор 5 до соприкосновения с образцом.
   
5. 
   Подключить чувствительные элементы (датчики сопротивления) датчика 6 (для измерения перемещении v) и динамометра 7 для измерения усилий Р) к двухкоординатному самописцу 8.
   
6. 
   Проверить и записать масштабы записи усилий Р и перемещений v.
   
7. 
   Включить самописец 8 и прогреть его до выхода на рабочий режим его электронных устройств.
   
8. 
   Включить машину и нагружать образец до разрушения (или обра- зования макротрещины от надреза).
   
9. 
   После разрушения образца выключить машину и самописец; снять полученную диаграмму Р-v.
   

Обработка результатов опыта.

1. 
   По виду диаграммы и анализу зоны разрушения установить вид разрушения (хрупкий или вязкий).
   
2. 
   Зарисовать диаграмму Р-v в журнале.
   
3. 
   Используя схему фиг. 6 установить нагрузку P_Ic или P'_Ic .
   

P'_Ic ).

4. 
   Определить критическое напряжение _с
   

(по нагрузкам P_Ic или

• 
  _ P_Ic  L
  

^c 4  W
Bh ²
или

• 
  _ P'_Ic L
  

^c 4  W

( W  - момент сопротивления).

6

5. 
   Рассчитать на основе формулы (8) величину
   

К_Iс  а_с

^КIc

Коэффициент а для

 / h 

принимается равным 1,3.

ния

6. 
   По максимальной нагрузке Р_с определить (см. п.п. 4 и 5) напряже-
   

_с , а по нему - критическое значение коэффициента интенсивности

напряжений

К_с .

7. 
   Определить отношение величин
   

^КIc ^Kc

и сделать заключение о

степени развития пластических деформаций в вершине трещины.

0. КОНТРОЛЬНЫЕ ВОПРОСЫ

1. 
   Какие типы оборудования нефтегазовых производств подлежат анализу прочности и ресурса?
   
2. 
   Назовите особенности конструктивных форм и условий нагружения оборудования.
   
3. 
   В чем состоит задача нормативных расчетов прочности и ресурса?
   
4. 
   С какой целью проводятся уточненные расчеты прочности и ресурса?
   
5. 
   Охарактеризуйте модели деформируемых твердых тел.
   
6. 
   Запишите основное уравнение состояния и назовите определяющие параметры уравнений.
   
7. 
   Как влияют температура и скорость деформирования на механические свойства?
   
8. 
   Охарактеризуйте статическое, длительное статическое и циклическое нагружение.
   
9. 
   Что такое обобщенная диаграмма циклического деформирования? Назовите основные параметры этих диаграмм.
   
10. 
    Запишите критериальные уравнения для статического, циклического и длительного статического нагружения.
    
11. 
    Как перераспределяются нагружения и деформации в зоне концентрации при переходе от упругого к пластическому деформированию?
    
12. 
    В чем состоят особенности деформирования и разрушения сварных соединений?
    
13. 
    Перечислите виды дефектов в элементах конструкций.
    
14. 
    Как изменяется распределение напряжений при уменьшении ра- диуса кривизны в вершине надреза?
    
15. 
    Что такое коэффициент интенсивности напряжений? Какова его размерность?
    
16. 
    В чем состоит сущность предельного состояния тела с трещиной?
    
17. 
    Как в опыте определяется критическая величина коэффициента интенсивности напряжений?
    
18. 
    Что такое раскрытие трещины?
    
19. 
    В чем состоят особенности деформирования и разрушения в зоне трещин упруго-пластического материала?
    
20. 
    Что такое диаграмма разрушения?
    
21. 
    Чем отличаются величины K_Ic и K_c?
    
22. 
    Для каких целей можно использовать характеристики K_Ic и K_c?
    
23. 
    Запишите условие для определения прочности и ресурса обору- дования нефтегазовых производств.
    
24. 
    Перечислите запасы прочности и ресурса и назовите диапазоны их изменения.
    

СПИСОК ЛИТЕРАТУРЫ

1. 
   Конструирование машин. Справочно-методическое пособие. – М.: Машиностроение, 1994. том 1. – 530 с. Том 2. – 624 с.
   
2. 
   Машиностроение. Энциклопедия. Том IV-I. Детали машин. Кон- струкционная прочность, трение, износ, смазка. – М.: Машиностроение, 1995. – 863 с.
   
3. 
   Безопасность России. Функционирование и развитие сложных народнохозяйственных, технических, энергетических, транспортных си- стем, систем связи и коммуникаций. – М.: МГФ «Знание», 1998, том 1. – 444 с., Том 2 – 410 с.
   
4. 
   Безопасность России. Безопасность трубопроводного транспорта. – М.: МГФ «Знание», 2002 – 749 с.
   
5. 
   Москвичев В.В., Махутов Н.А., Черняев А.П. и др. Трещиностой- кость и механические свойства конструкционых материалов. – Новоси- бирск: Наука, 2002. 333 с.
   
6. 
   Когаев В.П., Махутов Н.А., Гусенков А.П. Расчеты деталей машин и конструкций на прочность и долговечность. Справочник. – М.: Машино- строение, 1985. 223 с.
   
7. 
   Харионовский В.В. Надежность и ресурс конструкций газопрово- дов. – М.: Наука. – 2000. 407 с.
   
8. 
   Махутов Н.А. Деформационные критерии разрушения и расчет элементов конструкций на прочность. – М.: Машиностроение, 1981. – 272 с.