Расчёт движения колёсного робота. Расчет движения колесного робота. Практические задания 1 Расчет движения колесного робота
 Скачать 438.55 Kb. Скачать 438.55 Kb.
|
|
«Робототехника» Практические задания 1 Расчет движения колесного робота Движение по прямой или дуге на заданное расстояние, изменение положения захватного устройства – одни из базовых задач в робототехнике. Использование шаговых двигателей и сервомоторов (рис. 1) позволяет достигнуть высокой точности при таких перемещениях. Скажем, сервомоторы Lego EV3 имеют датчики с точностью измерения до 1 градуса.   а) б) Рисунок 1 – Примеры сервомотора (а) и шагового двигателя (б) для Arduino Сервоприводы отличаются тем, что содержат кроме самого двигателя токже датчик и электронный блок управления, сравнивающий внешний сигнал (задание) и текущие показания датчика. Блок управляет двигателем и поддерживает параметры движения, соответствующие заданию (например, приходящему с контроллера робота). Шаговые двигатели совершают вращение не непрерывно, а шагами. Каждый шаг составляет часть от полного оборота. Следовательно, чем больше шагов в обороте, тем большей точности можно достигнуть. Двигатель имеет несколько обмоток, при их последовательной активации под воздействием меняющегося магнитного поля статора ротор перемещается от одного положения к следующему, после остановки движения он фиксируется в последнем положении (рис. 2). 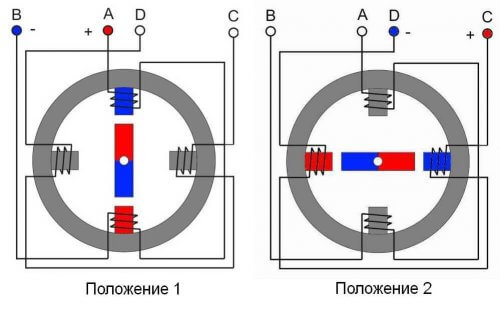 Рисунок 2 – Пример устройства шагового двигателя с 4 шагами Управлять движением сервомоторов и шаговых двигателей можно с помощью соответствующих функций, при этом настраивать можно разные параметры. Например, для сервомотора можно задавать угол поворота, количество оборотов, скорость вращения, для шагового двигателя – количество шагов, количество оборотов в минуту. При управлении движением колесного робота возникают следующие вопросы: Как рассчитать настройки так, чтобы робот проехал столько, сколько нужно? Как определить точность позиционирования? Цель данной работы – определить зависимости пройденного расстояния от параметров двигателей и колес робота и рассчитать значения, которые нужно внести в программу для движения на заданное расстояние. Введем обозначения: r – радиус колеса робота; v – скорость вращения сервопривода; Δc – погрешность сервопривода. Под ней будем понимать максимальное возможное отклонение от заданного угла. Т.е. если мы задали поворот на 20⁰ градусов, а Δc = 2⁰, то двигатель мог повернуться на угол от 18⁰ до 22⁰. N – число шагов на оборот у шагового двигателя; L – расстояние, которое должен проехать робот от начального до конечного положения; ΔL – погрешность положения робота. Под ней будем понимать максимальное возможное отклонение от заданного положения, например, если робот может проехать при одних и тех же настройках от 30 до 34 см, то ΔL = 2 см. γ – угол поворота сервопривода; t – время работы двигателя. Задания: Используя введенные выше обозначения, выполните в электронном виде описанные ниже задачи. Значения величин по вариантам представлены в таблице 1. Помните, что параметры движения зависят от радиуса колеса, также обращайте внимание на размерность величин. Необходимо, чтобы робот с сервомоторами проехал расстояние L. Выведите формулу для расчета угла поворота γ, на который должен повернуться двигатель. Выведите формулу для расчета ΔL при таком движении. Вычислите по выведенным формулам значения γ и ΔL. Определите, достаточна ли точность при движении на такое расстояния, если мы хотим, чтобы погрешность составила не более 5% от пройденного расстояния. Рассчитайте, при каком значении L1 погрешность составит 5% от L1. Мы задали сервоприводу определенную скорость v. Выведите формулу для расчета времени t, за которое робот с этой скоростью проедет расстояние L. Вычислите по этой формуле время. Мы управляем шаговым двигателем, задавая число шагов N. Выведите формулу для определения N, если нужно проехать расстояние L. Рассчитайте по этой формуле число шагов. Обратите внимание на то, что итоговое число шагов должно быть целым – шаги не делятся на более мелкие части. Выведите формулу для расчета ΔL при движении из п.6. Определите, достаточна ли точность при движении на такое расстояния, если мы хотим, чтобы погрешность составила не более 5% от пройденного расстояния. Рассчитайте, при каком значении L2 погрешность составит 5% от L2. Таблица 1 – Данные для расчетов
2 Расчет криволинейного движения Помимо движения по прямой мобильному роботу часто требуется поворачивать на месте на определенный угол или двигаться по дуге. Сложное движение по траектории неправильной формы может быть с некоторой точностью представлено как последовательность движений по дугам разного радиуса. В данном случае мы будем рассматривать симметричного мобильного робота с двумя большими колесами по бокам и маленьким сзади (для равновесия). Для упрощения будем считать, что маленькое колесо создает малое сопротивление при поворотах и пренебрежем его влиянием. Рассмотрим движение по дуге (рис. 3). 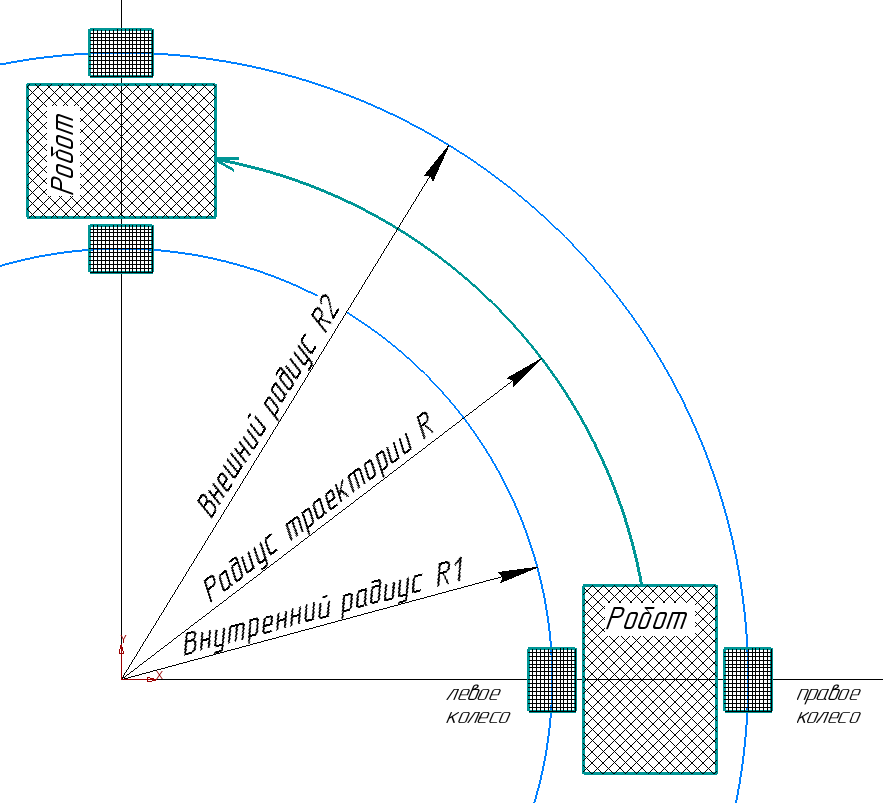 Рисунок 3 – Движение по дуге При движении по дуге радиуса влево R будем считать, что R – расстояние до центра робота, R1 – до центра левого колеса, R2 – до центра правого. При плавном повороте по дуге на 90⁰ окажется, что правое колесо, двигаясь по дуге большего радиуса, проделало больший путь, чем левое: 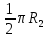 против против 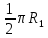 . Таким образом, можно установить прямую связь между отношением скоростей вращения левого и правого колес и радиусом поворота робота. . Таким образом, можно установить прямую связь между отношением скоростей вращения левого и правого колес и радиусом поворота робота.Если задать двигателям одинаковую по модулю, но противоположную по знаку скорость, мы добъемся вращения вокруг своей оси, радиус кривизны траектории каждого колеса будет равен при этом расстоянию от центра робота до центра колеса (рис. 4). Если задать разную скорость разного знака, то робот будет вращаться вокруг некоторой оси, находящейся между колесами (рис. 5). 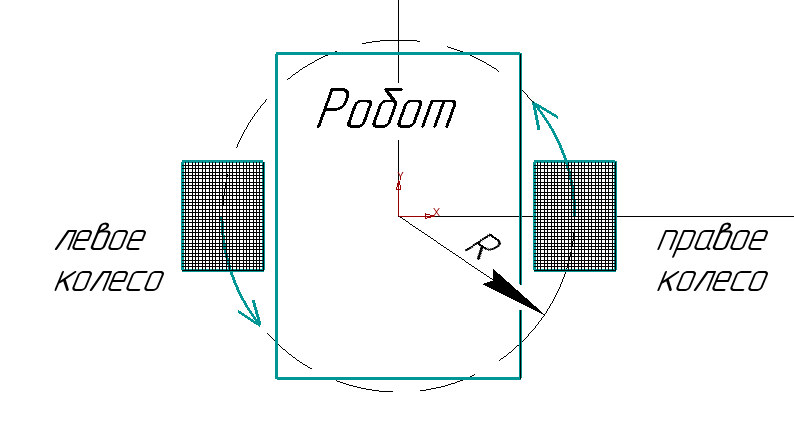 Рисунок 4 – Вращение вокруг своей оси 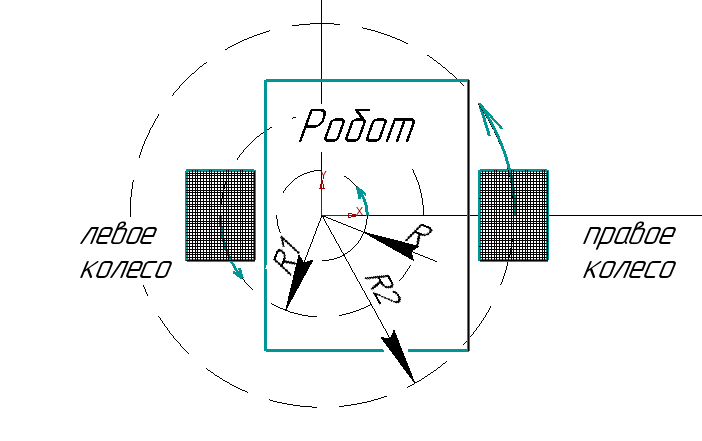 Рисунок 5 – Вращение вокруг некоторой оси Цель данной работы – определить зависимость радиуса дуги и угла поворота робота от параметров работы двигателей и рассчитать параметры, требуемые для движения по заданной дуге Введем обозначения: R – радиус кривизны траектории, по которой движется центр робота; v1 и v2 – скорости вращения левого и правого колес соответственно; α – угол, на который должен повернуться робот относительно своей оси; К – колея робота – расстояние между центрами его колес; t – время работы двигателя. Задания: Используя введенные выше обозначения, выполните в электронном виде описанные ниже задачи. Значения величин по вариантам представлены в таблице 2. Помните, что параметры движения зависят от радиуса колеса, также обращайте внимание на размерность величин – в том числе скорость вращения колес и скорость движения его центра связаны между собой, но выражаются в разных единицах. Выведите зависимость радиуса кривизны траектории R от скоростей вращения колес робота и его колеи К. Обратите внимание, что этот радиус не равен радиусам кривизны траекторий, по которым движутся колеса, но связан с ними. Вычислите по выведенной формуле значение R. Ответьте на вопрос: как изменится R, если мы увеличим скорости вращения обоих колес в два раза? Ответьте на вопрос: можно ли при вычислении по этой формуле определить, поворачивает робот влево или вправо? В какую сторону он поворачивает у вас? Проверьте свою формулу: подставьте v1 и 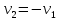 , что соответствует вращению относительно центра робота. Соответствует ли полученное значение R теории? , что соответствует вращению относительно центра робота. Соответствует ли полученное значение R теории?Проверьте формулу: подставьте v1 и 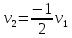 , что соответствует вращению относительно некоторой оси между колес робота. Сравните полученное значение R с , что соответствует вращению относительно некоторой оси между колес робота. Сравните полученное значение R с 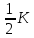 , соответствует ли оно теории? , соответствует ли оно теории?Выведите формулу зависимости скорости движения центра робота от скоростей вращения его колес. Рассчитайте значение. Выведите зависимость угла α, на который робот повернулся во время движения, от радиуса кривизны траектории R, времени движения t и скоростей вращения колес. Подсказка: робот движется по касательной к дуге, касательная перпендикулярна радиусу дуги, следовательно, угол поворота робота связан тем, какую часть окружности робот успел проехать по дуге. Рассчитайте угол поворота по полученной формуле. Таблица 2 – Данные для расчетов
|
