ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА. Практические заданияТеория вероятностей. Практических заданий по дисциплине теория вероятностей и математическая статистика

• Название: Практических заданий по дисциплине теория вероятностей и математическая статистика
• Анкор: ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
• Дата: 18.06.2021
• Размер: 22.76 Kb.
• Имя файла: Практические заданияТеория вероятностей.docx
• Тип: Задача; #218823

Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА



Группа ____________
Студент
_____________


МОСКВА 2021

Ответы на практические задания.
Задача 1.
Буквы, составляющие слово РАКЕТА, написаны по одной на шести

карточках; карточки перемешаны и положены в пакет.

1.1. Чему равна вероятность того, что, вынимая четыре буквы, ПОЛУЧИМ

слово РЕКА?

1.2. Какова вероятность сложить слово КАРЕТА при вынимании всех букв?
Решение:

1. 
   Рассчитаем вероятность появления нужной буквы (каждая буква вынимается при условии, что предыдущее событие уже произошло).
   

Вероятность того, что вытащим букву Р: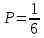



Вероятность того, что вытащим букву Е (из оставшихся 5-ти, 1 буква Е):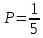



Вероятность того, что вытащим букву К (из оставшихся 4-х, 1 буква К):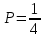



Вероятность того, что вытащим букву А (из оставшихся 3-х, 2 буквы А):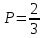



Вероятность событий что мы поочередно вынем буквы Р, Е, К, А:

2. 
   Рассчитаем вероятность появления нужной буквы (каждая буква вынимается при условии, что предыдущее событие уже произошло).
   

Вероятность того, что вытащим букву К: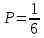



Вероятность того, что вытащим букву А (из оставшихся 5-ти, 2 буквы А):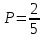



Вероятность того, что вытащим букву Р (из оставшихся 4-х, 1 буква Р):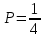



Вероятность того, что вытащим букву Е (из оставшихся 3-х, 1 буква Е):



Вероятность того, что вытащим букву Т (из оставшихся 2-х, 1 буква Е):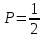



Вероятность появления последней буквы А равна 1.

Вероятность событий что мы поочередно вынем буквы К, А, Р, Е, Т, А:


Задача 2.

Дискретная случайная величина ξ задана следующим законом

распределения:

ξ	4	6	10	12
Р	0,4	0,1	0,2	0,3

Найти математическое ожидание, дисперсию и среднее квадратическое

отклонение.
Решение:

Математическое ожидание вычисляется по формуле: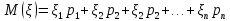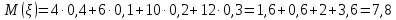




Дисперсия ищется по формуле: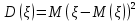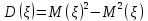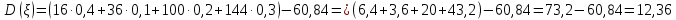






Среднеквадратическое отклонение:


Задача 3.

Возможные значения дискретной случайной величины равны: -2, 1, 4. При

условии, что заданы: математическое ожидание М(ξ) = 1.9, а также

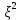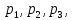М( ) = 7.3, найти вероятности которые соответствуют

дискретным значениям случайной величины.
Решение:

Так как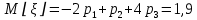







То получим следующую систему уравнений:



Решение находим по системе Гаусса: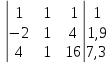


Ко второй строке прибавляем первую строку умноженную на 2, а к тертьей строке прибавляем первую строку умноженную на -4 и получаем: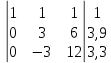



К третьей строке прибавляем вторую строку и получаем: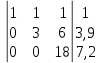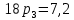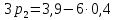



, тогда

, тогда



Ответ: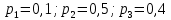