теория вероятности. Практическое задание по дисциплине Теория вероятностей математич. Практических заданий по дисциплине теория вероятностей и математическая статистика
 Скачать 21.61 Kb. Скачать 21.61 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Группа 20М171 Студент Серебряков А.А МОСКВА 2021 Задание №1 Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет. 1.1.Чему равна вероятность того, что, вынимая четыре буквы, ПОЛУЧИМ слово РЕКА? 1.2.Какова вероятность сложить слово КАРЕТА при вынимании всех букв? Решение: Введем в рассмотрение следующие события: A={получили слово РЕКА}, B={получили слово КАРЕТА}. Используя теорему умножения вероятности, получим: 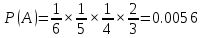 ; ;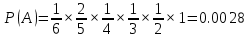 . .Ответ: 1)0.0056; 2)0.0028. Задание №2 Дискретная случайная величина ξ задана следующим законом распределения:
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение. Решение: Найдем заданные числовые характеристики: 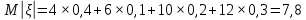 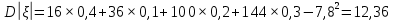 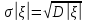 = =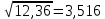 Ответ:  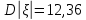 ; ;  . .Задание №3 Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание М ( 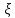 )=1,9, а также М( )=1,9, а также М(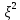 )=7,3, найти вероятности )=7,3, найти вероятности 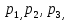 которые соответствуют дискретным значениям случайной величины. которые соответствуют дискретным значениям случайной величины.Решение: Так как: 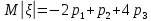 =1,9 , =1,9 ,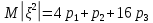 =7,3 и =7,3 и 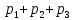 = 1, то получим: = 1, то получим: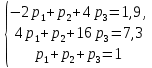 Найдем решение системы методом Гаусса: 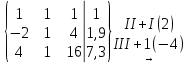 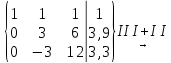 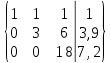 ; ;Ранг матрицы системы равен рангу расширенной матрицы, значит, система совместна. Тогда получим: 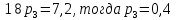 ; ; ; ;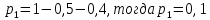 ; ;Ответ: 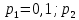 = 0,5 ; = 0,5 ; 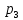 = 0,4. = 0,4. |
