Практическая работа. Задача по линейной оптимизации. Практическое задание 6
 Скачать 40.85 Kb. Скачать 40.85 Kb.
|
|
Федеральное государственное автономное образовательное учреждение высшего образования «Сибирский федеральный университет» Саяно – Шушенский филиал институт Гидроэнергетики, гидроэлектростанций, электроэнергетических систем и электрических сетей кафедра ПРАКТИЧЕСКОЕ ЗАДАНИЕ № 6 «Методы и средства научных исследований» наименование дисциплины «Графическое решение задачи линейного программирования» тема Вариант 3
Саяногорск 2019 Цель работы: найти оптимальный план работы энергосистемы, обеспечивающий максимум суммарного отпуска электроэнергии в стоимостном выражении графическим методом. Краткие теоретические сведения: Графически могут быть решены: • задачи, заданные в канонической форме с числом свободных переменных n – r ≤ 2; • задачи, заданные в стандартной форме, содержащие не более двух переменных; • задачи общего вида, которые после приведения к канонической форме будут содержать не более двух переменных. Решение задачи проходит в два этапа: построение области допустимых решений (ОДР) и нахождение в этой области оптимального решения. В первом случае задача не имеет решения из-за несовместности системы ограничений в ОДР; во втором случае задача всегда имеет оптимальное решение; в третьем случае, в зависимости от направления вектора С (от коэффициентов функции L), задача может иметь или не иметь решения. Последнее связано с неограниченным возрастанием (Lmax → ∞) или убыванием (Lmin → –∞) функции L в ОДР. Задача может иметь единственное оптимальное решение, совпадающее с одной из вершин области, и бесчисленное множество решений (альтернативный оптимум). В случае альтернативного оптимума и ограниченной области оптимальные решения соответствуют всем точкам отрезка, соединяющего две вершины области. В случае неограниченной области может оказаться, что среди множества оптимальных решений только одно совпадает с вершиной области. Условие задачи: Районная энергосистема включает в себя две тепловые электростанции. В качестве топлива на ТЭС могут использоваться уголь и газ. Известны запасы каждого вида топлива и удельный расход топлива на 1 МВтч электроэнергии в течение суток для каждой ТЭС, а также стоимость электроэнергии для каждой ТЭС. Найти оптимальный план работы энергосистемы, обеспечивающий максимум суммарного отпуска электроэнергии в стоимостном выражении. Исходные данные: Для варианта №3 примем следующие данные:
Ход работы: На первом этапе формирования математической модели сведем все исходные данные (численные значения параметров носят условный характер):
Введем обозначения искомых переменных: W1 – отпуск электроэнергии на ТЭС1; W2 – отпуск электроэнергии на ТЭС2. Целевая функция – максимальный доход энергосистемы от реализации отпущенной электроэнергии, что соответствует максимальному отпуску электроэнергии: F = 40W1+40W2 > max Система ограничений, связанных с имеющимися запасами топлива на ТЭС энергосистемы: 6W1 +5W2 ≤ 3000 5W1 + 7W2 ≤ 3500 Простейшие граничные условия в виде не отрицательности переменных: W1≥0, W2≥0. Алгоритм графического метода сводится к следующим этапам. 1. Построение области допустимых решений (ОДР): отобразим графически на плоскости неравенство, для этого перейдем к уравнению вида: 6W1 + 5W2 ≤ 3000 которое представим графически прямой 1 на рис. по точкам (W1 = 500, W2 = 0) и (W1 = 0, W2 = 600). аналогичные построения проведем для второго неравенства – линия 2, по точкам (W1 = 700, W2 = 0) и (W1 = 0, W2 = 500); 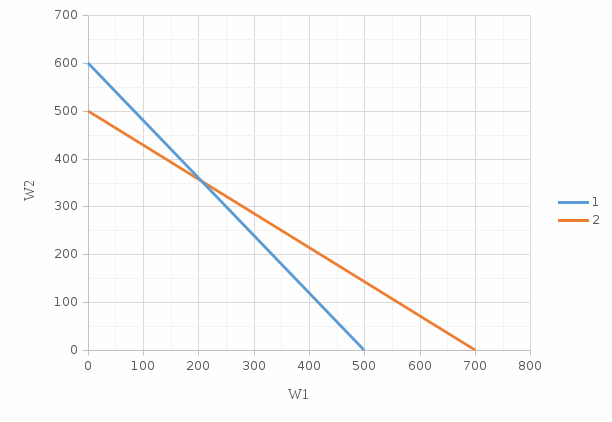 Рисунок 1. Построение области допустимых решений 2. Построение графика целевой функции. Графически видно, что оптимизационная задача имеет множество допустимых решений, из которых требуется найти оптимальное, удовлетворяющее в данном случае максимуму целевой функции. Для графического представления целевой функции зададимся произвольным значением F = 20000 и построим линию 3, которая называется линией уровня целевой функции: F = 40W1 + 40W2 = 20000 по точкам (W1 = 0, W2 = 500) и (W1 = 500, W2 = 0). Возможное увеличение целевой функции связано с удалением прямой от начала координат. Убедимся в этом, построив еще одну линию уровня для значения F = 22550 – линия 4. по точкам (W1 = 0, W2 = 563,75) и (W1 = 563,75, W2 = 0). 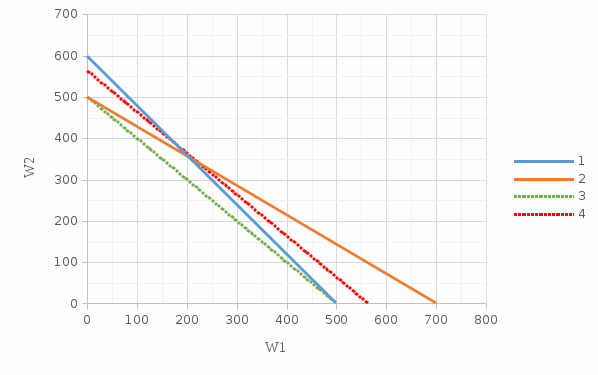 Рисунок 2. Построение графика целевой функции Исходя из графика найдём отпускаемую электроэнергию: Отпуск энергии ТЭС1 (W1) = 200 МВт. Отпуск энергии ТЭС2 (W2) = 360 МВт. Доход от реализации электроэнергии равен: F= 22400 тыс.руб. Вывод: Лабораторная работа была выполнена графическим методом, который позволяет, применяя не большие расчеты по графику определить искомые величины. Этот метод имеет свои недостатки в плане погрешностей при взятии показаний с графика, что является недопустимым при решении серьезных задач. В ходе решения были получены следующие результаты: отпуск энергии ТЭС1 = 360 МВт, отпуск энергии ТЭС2 = 200 МВт, доход от реализации электроэнергии равен: 22400 тыс. руб. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
