Статистика Интервальный ряд. ПЗ тема Интервальный ряд. Практическое занятие Определение средних и структурных показателей для интервального рядя Тема 1 Теоретический материал 1 Задание 4 Методическийе рекомендации
 Скачать 105 Kb.
|
ТемаПрактическое занятие «Определение средних и структурных показателей для интервального рядя»Тема 1 Теоретический материал 1 Задание 4 Методическийе рекомендации Изучить теоретический материал с практическим примером Решить задачу №1 Теоретический материалМетодика расчета средней величины зависят от поставленной цели исследования, от вида и взаимосвязи изучаемых признаков, а также от характера исходных данных. В отличие от дискретных рядов распределения определение моды и медианы по интервальным рядам требует проведения дополнительных расчетов. Рассмотрим пример о распределении кредитных организаций по величине активов.
Интервал с границами 135-145 в данном распределении будет модальным, так как он имеет наибольшую частоту. Определим моду:  Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит ½ суммы накопленных частот. Мы определили, что медианным является интервал с границами 135-145 . Проведем расчет медианы: 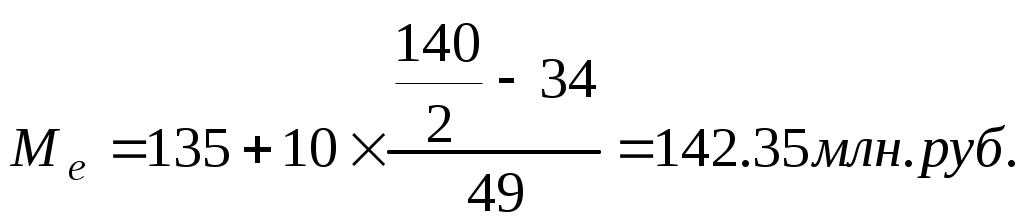 Рассмотрим пример распределения коммерческих банков по объему активов. В таблице 5 представлен расчет данных, которые необходимы для определения показателей степени вариации и характеристик формы распределения.
Как видно из формул, для расчета показателей вариации на основе интервального ряда необходимо использовать середину интервала и предварительно определить среднюю величину изучаемого признака. 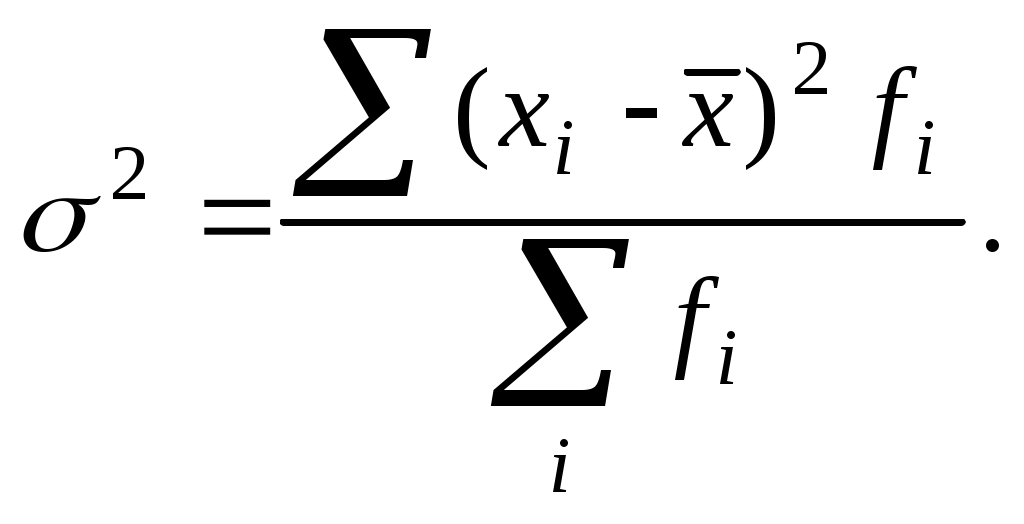  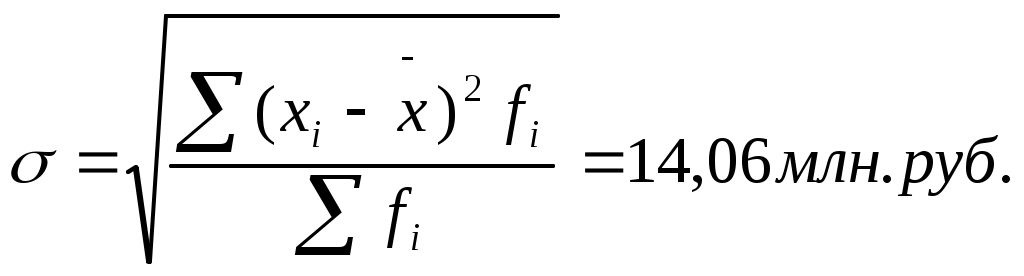 ; ;  ; ;      На основе рассчитанных обобщающих характеристик статистической совокупности коммерческих банков можно сделать следующие выводы: средний объем активов кредитной организации составляет 143,3 млн. рублей, а показатели вариации: среднее линейное отклонение – 11,15 млн. рублей; среднее квадратическое отклонение- 14,06 млн. руб., тогда коэффициент вариации равен  , следовательно, изучаемая совокупность банков является однородной по объему активов; асимметрия имеет несущественный характер, распределение является более плосковершинным, чем нормальное, отклонение от нормального распределения по показателю эксцесса является существенным. Для измерения вариации альтернативного признака, которым свойственны лишь два противоположных варианта, рассчитывается так называемая дисперсия доли. Доля единиц (частость), обладающих данным признаком, обычно обозначается p; доля единиц не обладающих данным признаком, обозначается q . Допустим, при обследовании 1000 коммерческих банков 800 из них являются универсальными. Определите дисперсию и среднее квадратическое отклонение доли универсальных банков. Решение: В нашем примере доля единиц, обладающих изучаемым признаком, т.е. доля универсальных банков, равна: p=800:1000=0,8 или 80%. Следовательно, 20% банков не обладали изучаемым признаком. Следовательно, дисперсия доли универсальных банков равна  Среднее квадратическое отклонение:  ЗаданиеЗадача 1По данным выборочного обследования получено следующее распределение работников по размеру заработной платы.
Рассчитайте: Среднюю заработную плату одного работника. Показатели вариации и формы распределения. Построить график. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
