Практическое задание Корпоративные финансы docx. Практическое занятие Стоимость заемного капитала Задание 1
 Скачать 71 Kb. Скачать 71 Kb.
|
МОСКВА 2022 Практическое занятие 2. Стоимость заемного капитала Задание 1. Вам поручено провести анализ досрочно погашаемой корпоративной облигации с номиналом 1000 рублей и 12% ставкой купона, который выплачивается раз в год, со сроком до погашения 20 лет и условием досрочного выкупа не ранее, чем через 4 года по курсу 112% номинала. Текущий курс облигации 116% от номинала. Требуется определить: a. текущую доходность облигации b. приблизительную доходность к погашению c. полную доходность к погашению d. приблизительную доходность к досрочному погашению (отзыву) Решение: a. текущая доходность облигации определяется по формуле: где С – купон С=N×g, Р – текущая цена облигации; g – процент по купону; N – номинал С = 1000 ×0,12 = 120 руб. b. приблизительная доходность к погашению определяется по формуле: где F – номинальная стоимость облигации. P – цена, уплаченная за облигацию. n – количество лет до погашения облигации 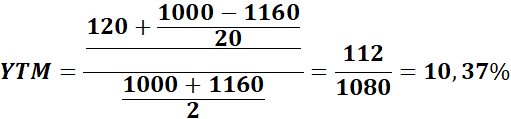 c. полная доходность к погашению рассчитывается по формуле: Под полной доходностью к погашению понимаем точно найденную через решение уравнения величину, где в качестве неизвестной имеем YTM. Не имеет смысла решать уравнение d. приблизительную доходность к досрочному погашению (отзыву) 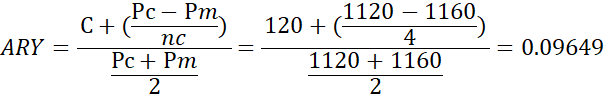 Задание 5. 1 000 рублевая облигация с 8 - процентным купоном продается на рынке с дисконтом в 10%, со сроком обращения 3 года. Определите текущую доходность облигации и доходность к погашению. Решение: 1. Рассчитаем текущий доход облигации по формуле: Dm = (N * r) / 100%, где N – номинальная цена облигации; r – годовая процентная ставка. Dm = (1000*8)/100=80 (руб.) 2. Рассчитав текущий доход, можно рассчитать текущую доходность облигации по формуле: dm = Dm / (B * 100%), где В –цена покупки. Цена покупки в данном случаи составляет 900 руб., т.к. облигация приобретена с дисконтом 10%. dm = 80/(900*100)=8,9 (%) Таким образом, текущая доходность облигации составляет 8,9% Практическое занятие 2. Стоимость собственного капитала Задание 1. Западноевропейская телекоммуникационная компания выплатила в 2015г дивиденд на акцию 0.72 евро, и при этом ее прибыль на акцию равна 1.25 евро. В течение последних 5 лет прибыль на акцию росла на 12% ежегодно, но ее темп снизится равномерно в течение предстоящих 10 лет до уровня 5%. Коэффициент выплаты дивидендов сохранится неизменным. Требуемая доходность инвестиций в акции этой компании 9%. Текущий курс акций 33.40 евро. Определите: a. Подлинную стоимость обыкновенной акции компании b. Дайте развернутый комментарий полученному результату. Какую инвестиционную стратегию вы бы рекомендовали индивидуальному инвестору, не склонному к риску? Двухфазовая модель роста предполагает, что для корпорации можно выделить две фазы развития, для которых характерен стабильный рост дивидендов (или иных определяющих параметров. В первой фазе для корпорации характерен быстрый (экстраординарный) рост дивидендов, затем на второй фазе возможности роста снижаются и приближаются к темпам роста экономики в целом. Подлинная стоимость обыкновенной акции компании может быть найдена по модели Гордона: Первая фаза растущая (стабильная): Р = = = 18.9 евро D – последние выплаченные дивиденды g - темпы роста через n лет, действующие после этого вечно. r – требуемая норма доходности Вторая фаза – экстраординарного роста: = = =6.3 евро Подлинная стоимость обыкновенной акции компании = 18.9 + 6.3 = 25.2 евро Допущение относительно постепенного снижения темпов роста со временем может привести к созданию полезной модели для описания фирм, которые быстро растут в настоящий момент, но, в соответствии с ожиданиями, темпы их роста должны постепенно падать по мере увеличения размеров этих фирм и потери имеющихся у них конкурентных преимуществ. Однако предположение о постоянстве коэффициента выплат делает эту модель нерабочей в отношении тех фирм, которые выплачивают невысокие дивиденды или вовсе не выплачивают их в настоящее время. Таким образом, данная модель, требующая одновременно высокого роста и высоких дивидендов, может иметь ограниченное применение. | ||||||||||||||||||||||||||
