Математическая логика. Практика Построение таблицы истинности. Необходимо знать Пример Домашнее задание 1 (построить таблицу истинности и сделать вывод о выводимости из множества посылок заключения) 1) 2) Минимизация формул.

• Название: Практика Построение таблицы истинности. Необходимо знать Пример Домашнее задание 1 (построить таблицу истинности и сделать вывод о выводимости из множества посылок заключения) 1) 2) Минимизация формул.
• Анкор: Математическая логика
• Дата: 22.02.2023
• Размер: 1.91 Mb.
• Имя файла: PRAKTIKA_1__tablitsa_istinnosti_minimizatsia.docx
• Тип: Документы; #950752

Практика 1.

Построение таблицы истинности.

Необходимо знать: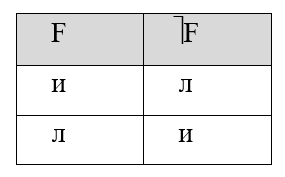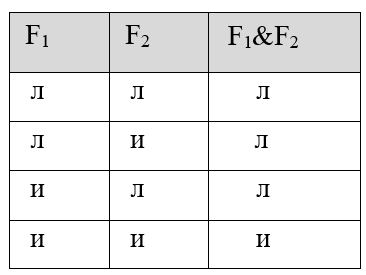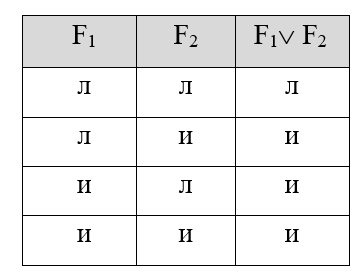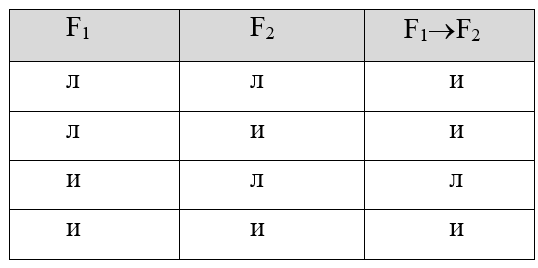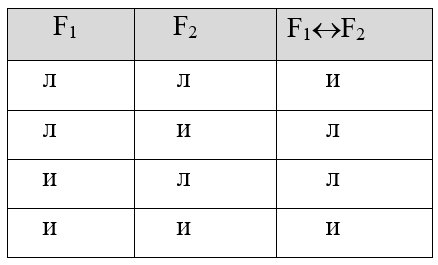





Пример: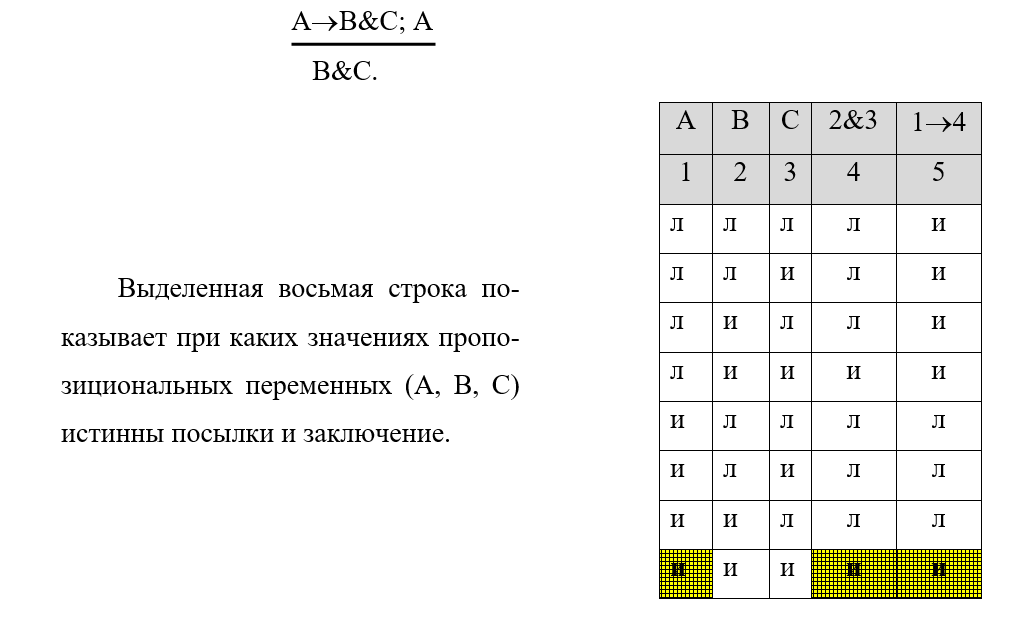


Домашнее задание №1 (построить таблицу истинности и сделать вывод о выводимости из множества посылок заключения):

1)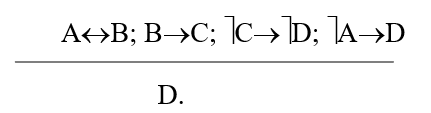

2)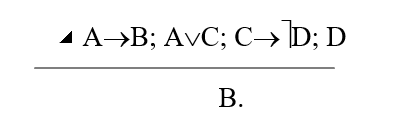

Минимизация формул.

При записи сложных формул следует помнить, что

1) каждое вхождение логической связки “” относится к пропозициональной переменной или формуле, следующей непосредственно за логической связкой справа;

2) каждое вхождение логической связки “” после расстановки скобок связывает пропозициональные переменные или формулы, непосредственно окружающие логическую связку;

3) каждое вхождение логической связки “” после расстановки скобок связывает пропозициональные переменные или формулы, непосредственно окружающие эту связку и т.д.

При использовании этих правил к одной и той же формуле скобки следует расставлять постепенно, продвигаясь слева направо.

Логические связки по силе и значимости могут быть упорядочены так: ; ; ; ; . То есть самой сильной связкой является отрицание, затем коньюнкция, дизьюнкция, импликация и, наконец, эквиваленция. Зная правила о силе логических связок, можно опускать те пары скобок, без которых ясен порядок исполнения логических операций.





Домашнее задание №2: Дана формула F=F1F2F3F1F3F1. Необходимо расставить все скобки.



Эквивалентные преобразования основных логических операций: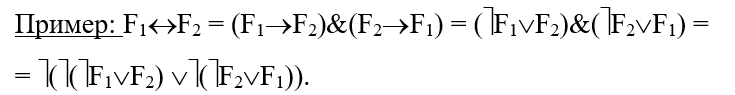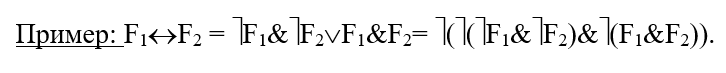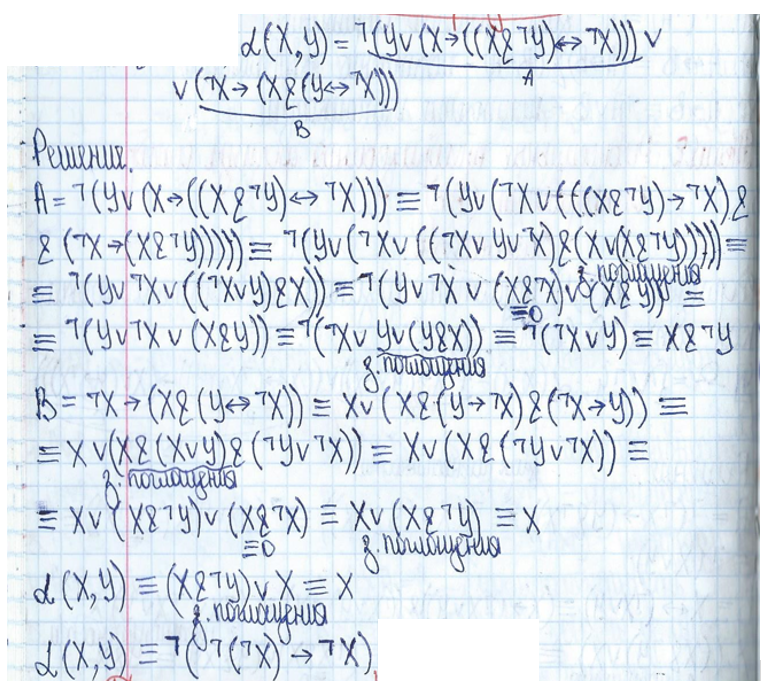








Домашнее задание №3:





­­­­­­­




(пример заданий из контрольной работы)

Высказывания, из которых делают вывод новых высказываний, называют посылками, а получаемое высказывание – заключением.
{AB; AC; BD} CD

а. Таблица 1 – Таблица истинности логического выражения

H= AB, Е= AC; M= BD; N= CD

A	B	C	D	AB	AC	BD	CD
				H	Е	M	N
0	0	0	0	0	1	1	0
0	0	0	1	0	1	1	1
0	0	1	0	0	1	1	1
0	0	1	1	0	1	1	1
0	1	0	0	1	1	0	0
0	1	0	1	1	1	1	1
0	1	1	0	1	1	0	1
0	1	1	1	1	1	1	1
1	0	0	0	1	0	1	0
1	0	0	1	1	0	1	1
1	0	1	0	1	1	1	1
1	0	1	1	1	1	1	1
1	1	0	0	1	0	0	0
1	1	0	1	1	0	1	1
1	1	1	0	1	1	0	1
1	1	1	1	1	1	1	1

Смотря на строки 6,8,11,12,16 таблицы истинности, в которых посылки H, Е и M истинны, видно, что заключение N тоже истинно. Поэтому можно сделать вывод, что данное заключение выводимо из данного множества посылок.

б. Минимизация формул:

H= AB

Е= AC = ¬ A ∨ С

M= BD = ¬ B ∨ D

N= CD