230101_ВС_ЛР. Практикум для студентов всех форм обучения специальности 230101 Вычислительные машины, комплексы, системы и сети (8, 9 семестры)
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
Лабораторная работа №3Тема работы: "Графы" Краткий справочный материал и примеры Принцип представления структуры в виде графа весьма прост. Элементам системы при решении одних задач ставят в соответствие ребра графа, а связям — вершины графа. При решении других задач поступают иначе: элементам ставят в соответствие вершины графа, а связям — ребра графа. Граф, полученный в первом случае, называется реберным, во втором случае, — вершинным. Рассмотрим некоторые основные определения и понятия из теории графов, необходимые при решении задач структурного анализа БСУ. Определение графа, виды графов Пусть определено некоторое множество элементов V. Граф G = G (V) считается определенным, если задано некоторое семейство сочетаний элементов или пар вида Е = (а, b), где а, b € V, указывающее, какие элементы считаются связанными. В соответствии с геометрической интерпретацией пара Е = (а, Ь) называется ребром, а элементы а, b — концевыми точками ребра или вершинами. Если порядок расположения концов безразличен, т. е. если Е = (а, b) = (b, а), то говорят, что Е есть неориентированное ребро; если же этот порядок важен, то Е называют ориентированным ребром — дугой; при этом а называют начальной вершиной, а b-конечной вершиной. В теории графов принята также следующая терминология: ребро Е инцидентно вершинам а, b, а вершины а, b инцидентны ребру Е. Граф, составленный только из неориентированных ребер, называется неориентированным, а граф, составленный только из ориентированных ребер, ориентированным. Графы, у которых часть ребер ориентированна, часть — неориентированна, называются смешанными. Неориентированный граф G может быть превращен в ориентированный при помощи процесса удвоения, состоящего в замене каждого ребра Е парой ребер с теми же концами и приписывании им противоположных ориентации. Граф называется конечным, если число ребер конечно, и бесконечным — в противном случае. Граф, состоящий из изолированной вершины, называется нуль-графом, а граф, ребрами которого являются всевозможные пары для двух различных вершин а, b из V, называется полным графом. В ориентированном полном графе имеются пары ребер по одному в каждом направлении, соединяющие любые две различные вершины (а, b). Способы формализованного задания графа А. Графическое представление. Данный способ является наиболее наглядной формой представления отношений между элементами, однако он не может быть использован при решении задач структурного анализа с использованием ЭВМ. Б. Матричное представление. Существуют различные формы матричного представления графа G = G (V). Матрица смежности вершин для неориентированного графа имеет вид А = |aij|, где n — число вершин в графе, а элементы аij определяется следующим образом: При этом предполагается, что нумерация вершин графа уже проведена. Для неориентированного графа матрица смежности является симметрической, что следует учитывать при использовании ЭВМ для компактного использования оперативной памяти в задачах структурного анализа. В матрице смежности вершин для ориентированного графа А = |aij| определяется следующим образом: Матрица смежности вершин А является матрицей непосредственных путей графа, имеющих длину, равную 1. Общее число транзитных путей от вершины i к вершине j длиной k может быть получено в результате возведения в k-ю степень матрицы А. Степень вершины Число ребер, инцидентных вершине неориентированного графа, называют степенью вершины. Число дуг ориентированного графа, которые имеют своей начальной вершиной вершину i, называют полустепенью исхода вершины i. Аналогично, число дуг, которые имеют своей конечной вершиной вершину j, называют полустепенью захода вершины j. При проведении структурного анализа систем очень часто необходимо располагать методикой, позволяющей определять некоторые структурные характеристики систем и давать им количественную оценку. Целесообразность определения таких характеристик состоит в том, что уже на ранней стадии проектирования появляется необходимость оценивать качество структуры системы и ее элементов с позиций общего системного подхода. Рассмотрим некоторые из них. Связность структуры Данная количественная характеристика позволяет выявить наличие обрывов в структуре, висящие вершины и др. Наиболее полно количественно связность элементов ориентированного графа определяется матрицей связности С = || Сij ||. Элементы матрицы С можно вычислить на основе матрицы Элемент Сij = 1, если Сij = 0, если Структурная избыточность Структурный параметр, отражающий превышение общего числа связей над минимально необходимым в неориентированных графах, будем называть структурной избыточностью R. Cтруктурная избыточность R определяется следующим образом: 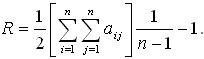 Данная структурная характеристика используется для косвенной оценки экономичности и надежности исследуемых систем. Для систем с максимальной избыточностью, имеющих структуру типа «полный граф», R > 0; для систем с минимальной избыточностью R = 0; для систем несвязных R < 0. Таким образом, система с большей избыточностью R потенциально более надежна. Задание Задание включает в себя следующие пункты: • Составить матрицу соответствующего графа (по вариантам). • Реализовать функцию (для уже имеющегося матричного аппарата) подсчета числа транзитных путей от вершины i к вершине j длиной k. • Реализовать функцию (для уже имеющегося матричного аппарата) подсчета полустепени исхода вершны i. • Реализовать функцию (для уже имеющегося матричного аппарата) подсчета полустепени захода вершны i. • Реализовать процедуру расчета матрицы С. • Реализовать процедуру расчета структурной избыточности R. Варианты 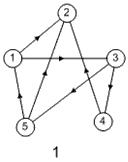 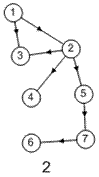 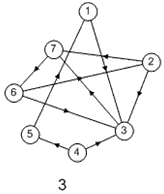 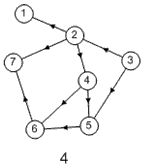 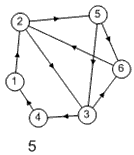 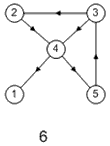 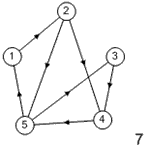 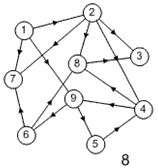 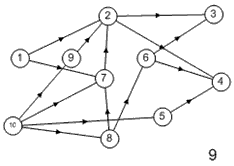 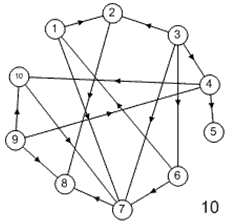 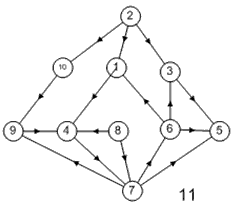 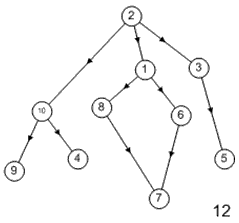 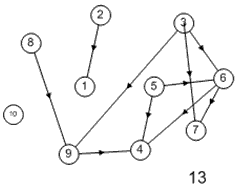 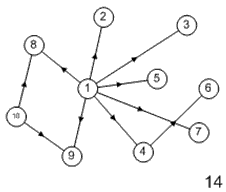 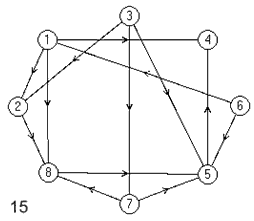 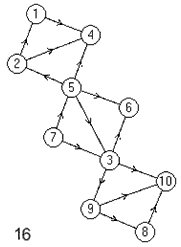 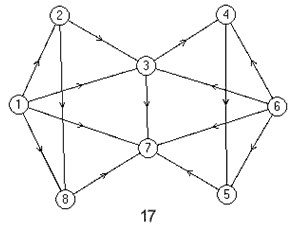 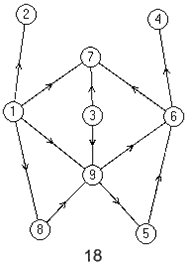 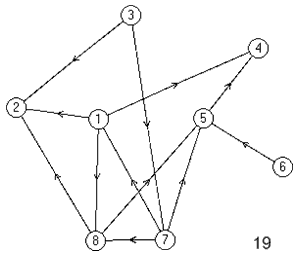 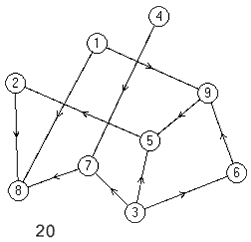 |
