230101_ВС_ЛР. Практикум для студентов всех форм обучения специальности 230101 Вычислительные машины, комплексы, системы и сети (8, 9 семестры)
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
Лабораторная работа №1Тема работы: "Упорядочивание (сортировка) массивов" Краткий справочный материал и примеры Выполнение лабораторной работы направлено на освоение основных приемов использования массивов, методов доступа к элементам массивов, их реорганизации и модификации. В качестве практической проблемы, требующей решения, рассматривается известная задача сортировки (упорядочивания) массива в порядке возрастания (убывания) его элементов. При решении этой задачи требуется исходный массив, содержащий произвольные целые числа, преобразовать к виду, когда каждый элемент массива находится перед другим элементом этого массива, если его значение меньше (больше), чем значение сравниваемого элемента. В данной лабораторной работе необходимо изучить ряд известных алгоритмов сортировки и создать комплекс программ, реализующий • линейный поиск элемента в массиве; • метод двоичного поиска элемента в упорядоченном массиве; • метод сортировки выбором; • метод сортировки пузырьком; • метод сортировки включением; • метод быстрой сортировки. Разрабатываемый программный комплекс должен обеспечивать • вывод на экран меню; • ввод исходной информации; • формирования массивов с большим числом элементов; • выбор метода сортировки; • сортировку массива; • печать результата; • замеры времени выполнения сортировок массива. Демонстрация работоспособности разработанных программных средств должна обеспечивать два варианта контроля: контроль работоспособности каждого из методов и контроль временных характеристик всех реализованных методов. Данная задача представляет собой упрощенный учебно-ознакомительный вариант широко распространенной задачи сортировки, которая применяется в широком классе реальных задач, и умение и знание алгоритмов сортировки и их особенностей является необходимой частью образования специалиста по программному обеспечению. Наряду с ознакомлением с проблемой упорядочивания массивов и методами ее решения, выполнение работы направлено на достижение следующих учебно-методических целей: • приобретение навыков и приемов использования массивов, доступа к их элементам и преобразований массивов; • практическое освоение принципов модульного программирования (использование процедур и функций); • освоение и изучение встроенных функций языка Zonnon и модуля System (применение генератора псевдослучайных чисел и замеры датчиков времени); • получения навыков сравнительного анализа эффективности разных алгоритмов. Программа должна обеспечить сортировку массивов размером произвольной длины до 10000 элементов и выводить для контроля: - при небольшом количестве элементов (например, менее 20) - неупорядоченный массив и массив после сортировки для каждого из предложенных алгоритмов; - при значительном объеме данных (более 20) выводить время сортировки одного и того же массива для всех четырех предложенных алгоритмов. Содержимое массива рекомендуется формировать с помощью генератора псевдослучайных чисел, замеры времени производить средствами модуля System (Random, DateTime). В ходе выполнения лабораторной работы предполагается реализация методов линейного и двоичного поиска элемента массива и разработка программ для четырех широко используемых алгоритмов сортировки: • метод выбора; • метод пузырька; • метод включения; • метод быстрой сортировки. Для простоты изложения описания алгоритмов будут проводиться на примере задач сортировки массивов по возрастанию. Поиск элемента массива на основе линейного просмотра Результатом работы алгоритма линейного поиска значения Val в массиве А являются индекс Pos и логическая переменная ResultOk, которая принимает значение TRUE, если такой элемент содержится в массиве А, и FALSE - в противном случае. Индекс Pos принимает значение, равное номеру искомого элемента, если такой найден, и значение, равное -1 - в противном случае. Алгоритм линейного поиска Шаг 1. Полагается Pos:=-1 и ResultOk:=FALSE, и значение переменной цикла J:=0. Шаг 2. Если A[J]=Val, то переменным Pos и ResultOk присваиваются соответственно значения Pos:=J, ResultOk:=TRUE и алгоритм завершает работу. В противном случае значение переменной цикла увеличивается на единицу J:=J+1. Шаг 3. Если J < Last, где Last - число элементов массива А, то выполняется Шаг 2, в противном случае - работа алгоритма завершена. Конец алгоритма. 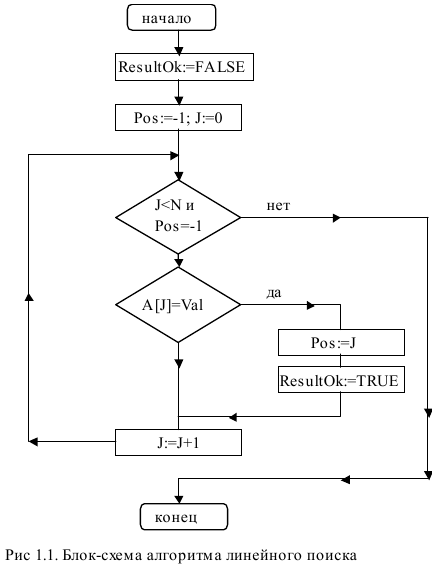 Метод двоичного поиска Результатом работы алгоритма является индекс Pos, показывающий на место в упорядоченном массиве А с номерами элементов от First до Last, на которое необходимо поставить значение Val так, чтобы вновь образованный массив остался упорядоченным. Формируется в качестве результата и логическая переменная ResultOk, которая принимает значение TRUE, если искомый элемент содержится в массиве А, и - FALSE - в противном случае. Алгоритм двоичного поиска Шаг 1. Пока справедливо условие First < Last, выполняется Шаг 2. Шаг 2. Вычисляется середина массива Middle:= (Last+First) div 2. Если Val равно А[Middle], то полагается First:=Middle и Last:=First , в противном случае проверяется условие - Val больше А[Middle]? Если это условие справедливо, то полагается First:=Middle+1, в противном случае полагается Last:=Middle-1. После чего управление передается на Шаг 1. Шаг 3. Полагается Pos:=First. Шаг 4. Проверка успеха поиска элемента Val в массиве. Полагается ResultOk:=FALSE. После чего проверяется, содержится ли элемент со значением Val в массиве, и при положительном ответе на этот вопрос переменной ResultOk присваивается значение TRUE. Конец алгоритма. 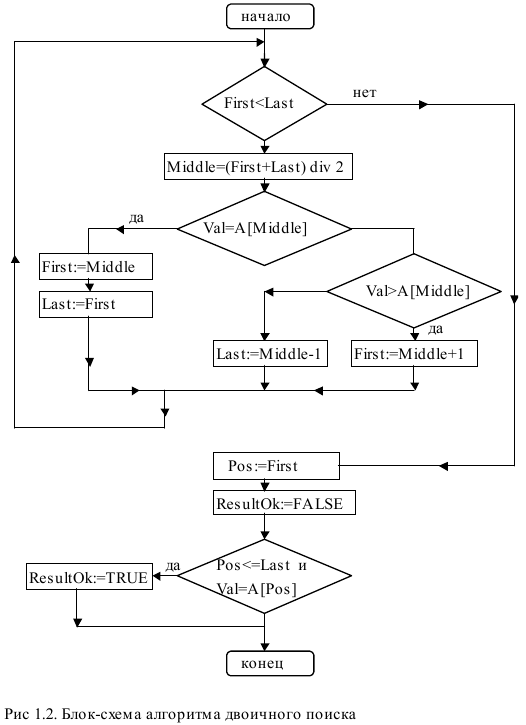 Метод сортировки выбором Исходный массив длиной N разбивается на две части: итог и остаток. Участок массива, называемый итогом, располагается с начала массива и должен быть упорядоченным, а участок массива, называемый остатком, располагается вплотную за итогом и содержит исходные числа не отсортированной части исходного массива. Пусть первый элемент остатка является J-ым элементом массива. Алгоритм сортировки выбором Шаг 1. Полагается J:=0, т.е. считается, что итоговый участок - пуст. Шаг 2. В остатке массива ищется минимальный и меняется местом с первым элементом остатка (J-ым элементом массива). После чего значение J увеличивается на единицу, тем самым расширяя итоговый участок массива (отсортированную часть исходного массива). Шаг 3. Если J < N-1, то повторяется Шаг 2. В противном случае - конец алгоритма, т.к. итог становится равным всему массиву. Конец алгоритма. 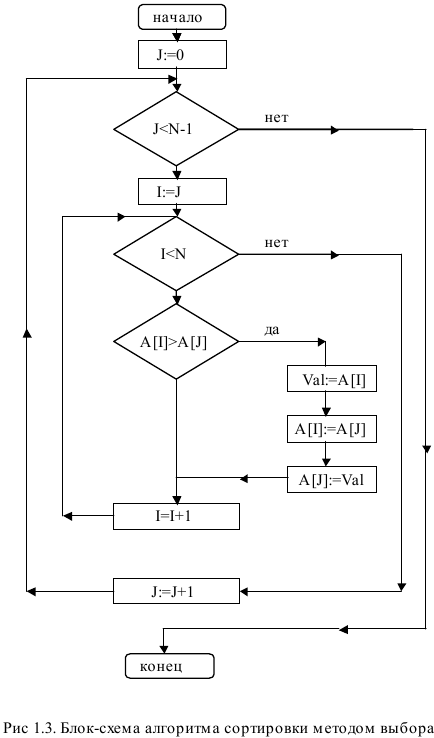 Метод сортировки пузырьком Аналогично, как и в методе выбора, исходный массив длиной N разбивается на две части: отсортированную (итог) и не отсортированную (остаток). Пусть первый элемент остатка будет J-ым элементом массива. Алгоритм сортировки пузырьком Шаг 1. Пусть J:=1 , т.е. итоговый участок состоит из одного элемента. Шаг 2. Берется первый элемент остатка и перемещается на место в итоговый участок массива так, чтобы итог остался упорядоченным. Первый элемент остатка назовем перемещаемым. Перемещение выполняется путем сравнения перемещаемого элемента с предшествующим ему элементом. Если предшествующий элемент меньше сравниваемого элемента, то процесс перемещения закончен. В противном случае сравниваемые элементы переставляются и, если элемент не достиг начала массива, то повторяется Шаг 2. Шаг 3. После того, как первый элемент остатка переместился в итоговый участок, увеличивается на единицу значение переменной J, тем самым увеличивая отсортированную часть массива. Если J < N, то управление передается на Шаг 2, в противном случае - работа алгоритма завершена. Конец алгоритма. 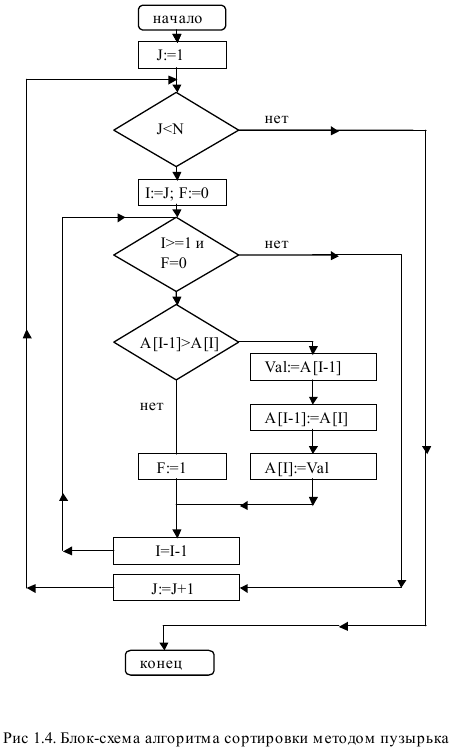 Метод сортировки включением Этот метод похож на метод пузырька. Происходит такое же разбиение массива на отсортированную и не отсортированную части, но перемещение первого элемента остатка на принадлежащее ему место в итоге делается не сравнением двух соседних элементов, а с помощью метода двоичного поиска, который удобно оформить в виде отдельной процедуры. Алгоритм метода включения Шаг 1. Пусть J=1 , т.е. итоговый участок состоит из одного элемента. Шаг 2. Берется первый элемент остатка и перемещается в отсортированную часть массива так, чтобы итоговый участок остался упорядоченным. Делается это с помощью обращения к процедуре двоичного поиска, которая в качестве выходного параметра дает номер элемента массива, на месте которого должен бы находиться перемещаемый элемент. Если этот номер указывает на место в итоговом участке массива, то сдвигаются все элементы итогового участка массива, начиная с этого номера на одно место вправо, а перемещаемый элемент ставится на освободившееся место. Шаг 3. После того, как первый элемент остатка переместился в итоговый участок, увеличивается на единицу значение переменной J, тем самым увеличивая отсортированную часть массива. Если J < N, то управление передается на Шаг 2, в противном случае - работа алгоритма завершена. Конец алгоритма.  Метод быстрой сортировки Исходным является массив А с номерами элементов от First до Last. В алгоритме используются еще два индекса массива, обозначенные как Index и ContrIndex. Первый из них всегда указывает на переставляемый элемент, а второй — на элемент, который сравнивается по значению с переставляемым. В процессе вычислений применяются переменная h (равная либо 1, либо -1) - шаг движения индексов навстречу друг другу, используемая для обозначения направления движения индекса ContrIndex, и логическая переменная Condition (равная либо TRUE, либо FALSE), используемая для изменения условия сравнения на противоположное при обратном движении индекса ContrIndex. Алгоритм быстрой сортировки Шаг 1. Если First >= Last, то происходит выход из алгоритма. В противном случае полагается h:=1, Condition:=TRUE, Index:=First, ContrIndex:=Last и делаются шаги: Шаг 2 - Шаг 3. Шаг 2. Пока Index не равно ContrIndex, делаются шаги: Шаг 2а -Шаг 2b. Шаг 2а. Если справедливо ((A[Index]>A[ContrIndex])=Condition), то переставляются как сами элементы, на которые указывают Index и ContrIndex, (Val:=A[Index], A[Index]:=A[ContrIndex], A[ContrIndex]:=Val), так и сами вспомогательные индексы массивов (Val:=Index, Index:=ContrIndex, ContrIndex:=Val). Затем меняется направление движения (h:= -h) и условие сравнения (Condition: = not Condition). В процессе таких перестановок слева от переставляемого элемента всегда будут находиться меньшие значения, а справа - большие значения. Шаг 2b. Сдвигается вспомогательный индекс массива ContrIndex навстречу индексу Index , т.е. ContrIndex:= ContrIndex +h. Шаг 3. Перед выполнением этого шага индексы Index = ContrIndex и элемент A[Index] находится на нужном месте. Т.е. исходный массив разбит на три части: часть массива до этого элемента, значения в котором меньше величины A[Index], часть массива после этого элемента с значениями большими значения A[Index] и сам этот элемент A[Index]. Поэтому для дальнейшего упорядочивания массива достаточно рекурсивно обратиться к алгоритму быстрой сортировки два раза: для первой и второй частей массива. Т.к. длина сортируемых участков массива уменьшается, то в итоге алгоритм конечен и после применения алгоритма массив будет полностью отсортирован. Конец алгоритма. 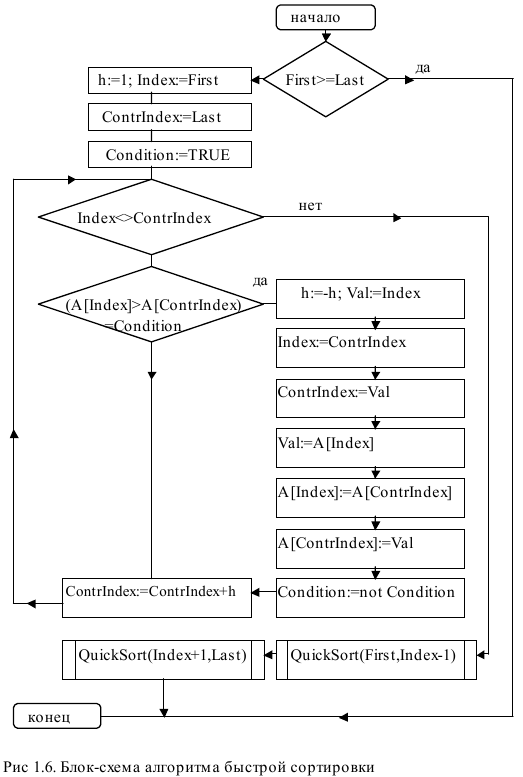 Задание В данной лабораторной работе требуется разработать программу, выполняющую следующие действия: 1. Ввод размера массива (или двух - в зависимости от задания) 2. Ввод исходного массива (массивов) 3. Вывод введенных массивов 4. Обработка массива (массивов) в соответствии с вариантом 5. Вывод получившихся массивов Замечания: 1) Количество элементов в исходных массивов до 20 ШТУК. 2) Элементами массивов являются целые числа. 3) Множества в программах не использовать. 4) После каждого изменения массивов новое состояние необходимо вывести на экран. 5) "Скопировать элементы" элементы из исходного массива добавляются в результирующий массив. 6) "Перенести элементы" элементы из исходного массива добавляются в результирующий массив, после чего удаляются из исходного. Варианты
|
