Показатели миграции населения
|
Абсолютные показатели
миграции населения
|
– численность прибывших в населенный пункт П;
– численность выбывших из населенного пункта В;
– абсолютный миграционный (механический) прирост (П-В).
|
Используются для характеристики механического движения
|
Объем миграции (валовая миграция, брутто-миграция)
|
– совокупность мигрантов по данной территории за определенный срок.
|
Характеризует миграционный оборот абсолютные размеры миграции.
|
Миграционный прирост(снижение) (сальдо миграции, чистая миграция, нетто-миграция)
|
– разность между числом прибывших и выбывших по данной территории за определенный период (П-В).
|
Показатель характеризует результат территориальных перемещений.
|
Коэффициенты прибытия, выбытия и миграционного прироста (интенсивность миграции)
|
вычисляются как отношение соответствующего числа прибывших, выбывших и миграционного прироста к среднегодовой численности постоянного населения по текущей оценке.
|
Коэффициент прибытия
|
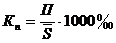
|
|
Коэффициент выбытия
|
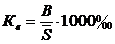
|
|
Коэффициент миграционного (механического) прироста
|
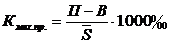
|
|
Коэффициент общего прироста населения
|
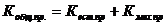
|
Он может быть исчислен несколькими способами.
|
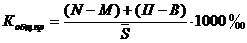
|
|
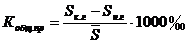
|
где Sк.г – численность населения соответственно на конец года и на начало года.
|
Интенсивность миграции
|
Общие коэффициенты интенсивности миграции могут быть рассчитаны по прибытию, выбытию, миграционному приросту и миграционному обороту на 1000 человек населения в расчете на год.
|
Характеризует частоту миграционных событий в совокупности населения за определенный период. Интенсивность миграционного оборота характеризует подвижность населения
|
Эффективность миграции
|
оценивается отношением миграционного прироста (сальдо миграции) к валовой миграции (объему миграции или сумме прибытий и выбытий), рассчитываются в процентах.
|
|
Результативность миграции
|
характеризуется числом выбывших в расчете на 1000 прибывших на данную территорию.
|
|
Б. Меры центральной тенденции
|
Средняя
|
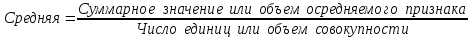
|
логическая формула
|
Средняя арифметическая
простая
|
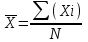
|
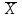 — среднее арифметическое; — среднее арифметическое;
Х – изменяющаяся величина признака;
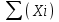 – сумма значений; – сумма значений;
N – количество значений
(число вариантов)
|
Средняя арифметическая
взвешенная
|
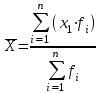
|
fi – вес каждого значения данных xi
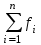 – сумма весов – сумма весов
|
Средняя гармоническая простая
|
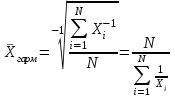
|
N – количество значений
(число вариантов);
Х – изменяющаяся величина признака;
∑ – сумма;
|
Средняя гармоническая взвешенная
|
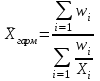
|
w – объемное значение признака: w=xf
|
Средняя геометрическая простая
|
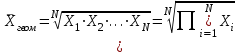
|
N – число вариантов
П – знак перемножения
fi – вес каждого значения данных xi
|
Средняя геометрическая взвешенная
|
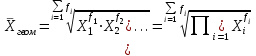
|
Средняя квадратическая простая
|
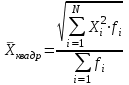
|
|
Средняя квадратическая
взвешенная
|
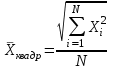
|
|
Мода
|
В дискретном ряду мода определяется как самое большое число
|
|
В интервальном ряду с равными интерваламимода определяется по формуле:
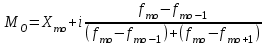
|
Хmo–нижняя граница модального интервала
i–величина модального интервала
Fmo– частота модального интервала
Fmo-1 – частота интервала, предшествующая модальному
Fmo+1 – частота интервала, следующая за модальным
|
В интервальном ряду с неравными интерваламимода определяется по формуле в два шага:
1) относительная частота (частость):
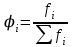
2) относительная плотность:
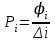
|
i– интервалы группировки
∆i– интервальная разность
fi– частота
φi–относительная частота (частость)
|
Медиана
|
В интервальном ряду медиана определяется по формуле:
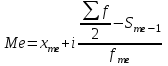
|
xme–нижняя граница медианного интервала
i–величина медианного интервала
∑f /2 – полусумма частот
Sme-1 – сумма накопленных частот до медианной частоты
fme –частота медианного интервала
|
В. Меры разброса
|
Отклонение:
|
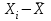
|
отклонения вариантов признака от его среднего значения
|
Размах вариации
|
R=Xmax - Xmin
|
разность между максимальным и минимальным значениями признака
|
Межквартильный размах:
|
Q = Q3 – Q1
|
расстояние между верхним и нижним квартилями
|
Нижний квартиль
Верхний квартиль
|
Q1 = ¼(n+1)
Q3 = ¾(n+1)
|
Нижний квартиль
Верхний квартиль
|
Среднее линейное отклонение (невзвешенное):
|
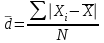
|
отклонения вариантов признака от его среднего значения, рассчитанные по модулю (т.е. без учета знаков «+» и «-»)
|
Взвешенное среднее линейное отклонение:
|
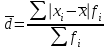
|
Дисперсия невзвешенная:
|
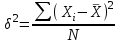
|
отклонения вариантов признака от его среднего значения, рассчитанные как средний квадрат отклонений
|
Дисперсия взвешенная:
|
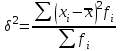
|
Стандартное отклонение:
|
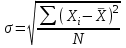
|
квадратный корень из частного от деления суммы квадратов всех вариант на число единиц совокупности
или
стандартное отклонение есть корень из дисперсии
|
Стандартное отклонение:
(формула, удобная для расчетов)
|
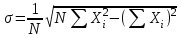
|
Стандартное отклонение взвешенное:
|
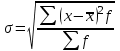
|
Коэффициент вариации:
|
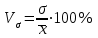
|
процентное отношение среднего квадратического отклонения к средней арифметической
|
Линейный коэффициент вариации:
|
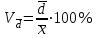
или
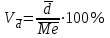
|
процентное отношение среднего линейного отклонений к средней арифметической
или медиане
|
Коэффициент осцилляции:
|
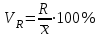
|
процентное отношение размаха вариации к средней арифметической
|
Г. Показатели динамики
|
Абсолютный прирост
|
y = yi – y1
|
представляет собой разность между двумя исходными уровнями, один из которых рассматривается как отчетная, оцениваемая величина, а другой принят за базу сравнения.
|
Абсолютный прирост
а) цепной
б) базисный
|
а) А1 = у1 - у0;
А2 = у2 – у1... Аn = уn - уn-1
б) А1 = у1 - у0;
А2 = у2 – у0... Аn = уn - у0
|
а) когда за базу сравнения берут каждый предыдущий уровень;
б) если для сравнения в
качестве базы берется один исходный уровень у0
|
Абсолютный рост
либо снижение преступности
|
Ар(с)п = Оп-Оп1,
|
где Ар(с)п - абсолютный рост или снижение преступности;
Оп - объем преступности за интересующий период;
Оп1 - объем преступности за аналогичный предыдущий период.
|
Коэффициент роста
(темп роста без %)
|
K = yi / y1
|
выражает отношения между собой двух уровней ряда — отчетного и базисного
|
Коэффициент роста
а) цепной
б) базисный
|
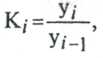 а) б) а) б)
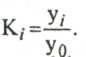
|
|
Темпы роста преступности
|
ТДП = (Оп/Оп1) х 100%
|
Оп - объем преступности за интересующий период;
Оп1 - объем преступности за аналогичный предыдущий период
|
Темп (процент)
прироста
|
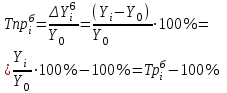
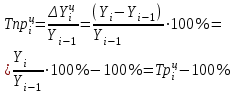
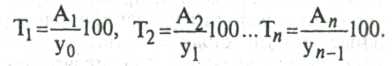
|
отношение цепного абсолютного прироста Аi к предыдущему уровню уi-1 , %
или отношение (обычно процентное) абсолютного прироста к уровню, взятому для сравнения.
Он может быть получен путем вычитания 100% из темпа роста. ТПР можно получить также путем деления абсолютного прироста на базисный уровень, по сравнению с которым рассчитан абсолютный прирост.
|
Темпы прироста (снижения) преступности
|
Тп(с)п = ТДП - 100%
|
Абсолютное значение одного процента прироста
|
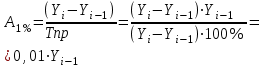
|
отношение абсолютного прироста к темпу прироста
|
Пункты роста
|
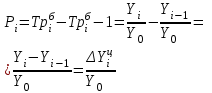
|
разность базисных темпов роста (прироста) смежных периодов
|
Темп наращивания
|
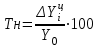
|
деление цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения
|
 Скачать 344.7 Kb.
Скачать 344.7 Kb.