ЛАБОРАТОРНЫЕ РАБОТЫ ПО АТОМНОЙ И КВАНТОВОЙ ФИЗИКЕ. Практикум по физике (атомная и квантовая физика) Направление подготовки 010700 (510400) Физика

• Название: Практикум по физике (атомная и квантовая физика) Направление подготовки 010700 (510400) Физика
• Дата: 24.05.2022
• Размер: 2.87 Mb.
• Имя файла: ЛАБОРАТОРНЫЕ РАБОТЫ ПО АТОМНОЙ И КВАНТОВОЙ ФИЗИКЕ.doc
• Тип: Практикум; #546914
• страница: 15 из 15

Метод полного поглощения.

Для β-частиц с энергией 0,7 МэВ<E<3 МэВ, хорошо оправдывается соотношение Физера:

, (5)

где ρ - в ,d _max – в см, E_макс – в МэВ.

Кривая поглощения (рис. 2) приближенно описывается экспоненциальным законом:

, (6)

где N₀ – число β-частиц до поглощения, N – число частиц после прохождения слоя d, μ – линейный коэффициент поглощения (см ^-1).Для определения μ необходимо выбрать на графике lnN=f(d) (см. рис. 3) примерно прямолинейный участок и из соотношения.

( )

определить данный коэффициент. При измерении толщины d в массовых единицах закон поглощения запишется:

, (7)

где - массовая толщина, - массовый коэффициент поглощения. Необходимость введения двух коэффициентов поглощения вызвана тем, что линейный коэффициент поглощения зависит как от природы поглощающего вещества, так и от граничной энергии β-спектраE_макс. Массовый коэффициент поглощения резко зависит от величины Е и примерно одинаков для химических элементов с близкими значениями Z.

Метод половинного поглощения.

Кроме изложенного выше метода полного поглощения, пользуются также методом половинного поглощения, который учитывает, что при малых и больших значениях d ход кривой поглощения отличается от экспоненциального закона (см. рис. 3). Этим методом производят измерение толщины слоя половинного поглощения. Слоем половинного поглощения dназывается такой с 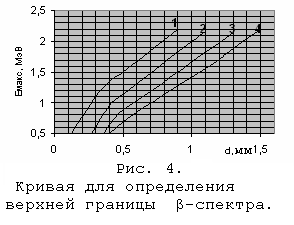лой, при прохождении которого интенсивность β-излучения уменьшается вдвое.

Все рассмотренные выше характеристики μ, μ΄, можно определить из экспериментальной кривой поглощения (рис. 2 и 3), где R – пробег β-частицы.

Для определения E_макс по графику N=f(d) определяют толщины слоев алюминия, ослабляющего излучение в 2¹, 2², …, 2^k раз. Связь между толщиной слоя алюминия d, ослабляющего в раза, и максимальной энергией β-спектра экспериментально изучена и представлена в виде кривых, приведенных на рис. 4. Каждая кривая на рис. 4 соответствует своему значению k. При k=1 скорость счета уменьшается в 2 раза, при k=2 – в 4 раза и т.д. Зная толщину d, уменьшающую скорость счета в 2 раза, по графику (см. рис. 4) можно определить значениеE_макс в МэВ.

Задание.

1. Подготовить лабораторную установку к работе, проверив работоспособность источника питания, секундомера и счетчика импульсов. Установить U= 450 В.

2. Измерить фон установки за t=5 мин. Он складывается из действия на счетчик:

5. 
   космического излучения;
   
6. 
   рассеянных частиц;
   
7. 
   тормозного излучения;
   
8. 
   β-лучей в спектре источника.
   

Для определения N_ф необходимо определить счет установки с фильтром, задерживающим все электроны (d=3 мм).

.

3. Снять кривую поглощения. Фольга располагается между счетчиками излучения и коллиматором. Нужная толщина фильтра достигается путем последовательного наложения алюминиевых пластинок друг на друга. Толщина пластинок измеряется микрометром. Толщину увеличивать от 0 до 3 мм, получить максимальное число точек. Начинать измерения при t=10(сек), затем увеличить время, набирая не менее 1000 импульсов в каждом измерении.

4. Заполнить таблицу 1.

Таблица 1.

№ опыта	толщина d, мм	Время измерения t, сек	N	n= , сек-1	lnn

5. Построить графики n=f(d) и lnn=f(d), отложив на них уровень фона.

6. По графику lnn=f(d) определить d_max.

7. Пользуясь соотношением ( ) рассчитать линейный коэффициент поглощения μ.По формуле рассчитать массовый коэффициент μ΄( ).

8. Оценить верхнюю границу β-спектра E_макс методами полного поглощения и половинного поглощения.

9. Сравнить полученные результаты с данными, известными из литературных источников.

10.Сформулировать выводы по работе.
Контрольные вопросы.

1.Виды радиоактивного распада.

2. распад и его закономерности.

3.Как объяснить непрерывный энергетический спектр электронов при распаде?

4.Какими основными механизмами объясняется поглощение электронов в веществе?

5.Что такое линейный и массовый коэффициенты поглощения?

6.В чём заключаются методы полного и половинного поглощения определения Е_max верхней границы β– спектра?

Литература.

1. 
   Савельев И.В., «Курс общей физики», т. 3,
   
2. 
   Сивухин Д. В., «Общий курс физики», т. V-2.