ЛАБОРАТОРНЫЕ РАБОТЫ ПО АТОМНОЙ И КВАНТОВОЙ ФИЗИКЕ. Практикум по физике (атомная и квантовая физика) Направление подготовки 010700 (510400) Физика
 Скачать 2.87 Mb. Скачать 2.87 Mb.
|
Задание.Ознакомиться с установкой, для чего изучить электрическую схему, разобраться в назначении всех элементов пульта управления. Найти цену деления каждого измерительного прибора при различных положениях переключателя пределов измерения. Увеличивая напряжение Uуск, убедиться в наличии максимумов напряжения U2 . Снять зависимость напряжения U2 от величины ускоряющего напряжения. Построить график зависимости U2=f(Uуск) и определить значение первого потенциала возбуждения. Определить длину волны излучения возбужденного атома исследуемого газа. Сформулировать выводы по работе. Контрольные вопросы.Сформулируйте постулаты Бора. Запишите правило частот Бора. Какое состояние атома называется основным? Какие возбужденными? Какие типы столкновений электронов с атомами возможны и как при этих столкновениях перераспределяется энергия между электроном и атомом? Объясните, почему опыты Франка и Герца подтверждают наличие дискретных уровней энергии атома. Как объяснить существование нескольких минимумов на графике U2=f(Uуск)? Как по графику U2=f(Uуск) определить величину первого потенциала возбуждения? Объясните, в чем заключается метод задерживающего потенциала. Литература.Савельев И.В. Курс общей физики.-М.: Высшая школа, 1979. т.Ш. ЛАБОРАТОРНАЯ РАБОТА №15Изучение вентильного фотоэффекта. Цель работы: ознакомление с вентильным фотоэффектом, исследование вольт-амперных характеристик вентильного фотоэлемента. Оборудование: 1. Источник света: лампа накаливания , U=3 В, св=1 кд. 2. Кремниевый фотоэлемент, площадь приемной части S=1,485·10-3 м2. 3. Магазин сопротивления Р-33 (099999) Ом. 4. Трансформатор. 5. Микроамперметр: предел измерений 100мкА. 6. Цифровой вольтметр Щ - 300. 7. Линейка. Краткая теория. Наиболее отчетливо полупроводники отличаются от проводников характером зависимости электропроводимости от температуры. Измерения показывают, что у полупроводников удельное сопротивление с увеличением температуры не растет, как у металлов, а, наоборот, чрезвычайно резко уменьшается. При температурах, близких к абсолютному нулю, удельное сопротивление полупроводников очень велико. Это означает, что при низких температурах полупроводник ведет себя как диэлектрик. Кремний – четырехвалентный элемент. Это означает, что во внешней оболочке атома имеются четыре электрона, сравнительно слабо связанные с ядром. Взаимодействие пары соседних атомов осуществляется с помощью парной электронной связи, называемой ковалентной связью. Каждый атом образует четыре связи с соседними, и любой валентный электрон может двигаться от одного атома к соседнему, дойдя до соседнего он может перейти к следующему, при этом, электрон не является свободным и прочно «привязан» к кристаллической решетке, и внешнее электрическое поле не оказывает заметного влияния на его движение. При нагревании кристалла кинетическая энергия валентных электронов повышается, и наступает разрыв отдельных связей. Некоторые электроны становятся свободными, подобно электронам в металле. При разрыве ковалентной связи образуется вакантное место недостающего электрона. Его называют дыркой. Дырка имеет избыточный положительный заряд (рис.1). Положение дырки в кристалле не является неизменным. Непрерывно происходит следующий процесс. Один из электронов, обеспечивающих связь атомов, перескакивает на место образовавшейся дырки и восстанавливает здесь электронную связь, а там, откуда перескочил этот электрон, образуется новая дырка. Таким образом, дырка может перемещаться по всему кристаллу в направлении противоположном движению электрона. Движение электронов и дырок в отсутствие электрического поля является хаотическим. В полупроводниках наряду с процессом генерации электронов и дырок идет процесс рекомбинации(исчезновение свободной пары электрон – дырка): электроны переходят из зоны проводимости в валентную зону, отдавая энергию решетке. 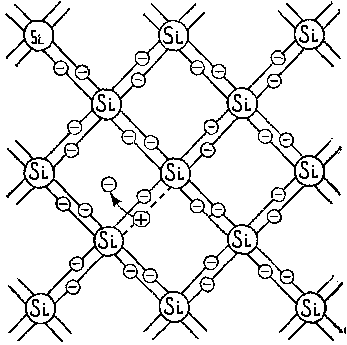 Рис. 1. Условная схема кристалла кремния. Электронно-дырочная проводимость получила название собственнойпроводимости.Собственная проводимость полупроводников обычно невелика, так как мало число свободных электронов. Существенная особенность полупроводников состоит в том, что в них при наличии примесей наряду с собственной проводимостью возникает примесная проводимость. Примесная проводимость полупроводников обусловлена наличием посторонних атомов в кристаллической решётке, а также определяется количеством и типами различных дефектов структуры кристалла. Наличие в полупроводнике примеси существенно изменяет его проводимость. Например, при введении в кремний примерно 0,001ат. % бора его проводимость увеличивается примерно в 106 раз. Примесную проводимость полупроводников рассмотрим на примере Si, в который вводятся атомы с валентностью, отличной от валентности основных атомов на единицу. Например, при замещении атома кремния пятивалентным атомом мышьяка (рис. 2) один электрон не может образовать ковалентной связи, он оказывается «лишним» и может легко покинуть атом, т. е. стать свободным. Образование свободного электрона не сопровождается нарушением ковалентной связи; следовательно, дырка не возникает. Избыточный положительный заряд, возникающий вблизи атома примеси, связан с атомом примеси и поэтому перемещаться по решетке не может. Таким образом, в полупроводниках с примесью, валентность которой на единицу больше валентности основных атомов, носителями тока являются электроны; возникает электронная примесная проводимость. Полупроводники с такой проводимостью называются электроннымиили полупроводниками n-типа. Примеси, являющиеся источниками электронов, называются донорами. 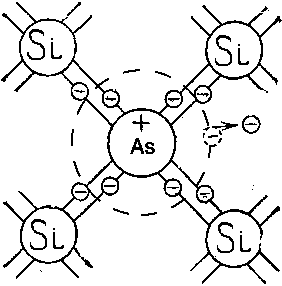 Рис. 2. Решетка кремния с примесью атомов мышьяка. Если предположить, что в решетку кремния введен примесный атом с тремя валентными электронами, например бор (рис. 3), то для образования связей с четырьмя ближайшими соседями у атома бора не хватает одного электрона, одна из связей остается неукомплектованной и четвертый электрон может быть захвачен от соседнего атома основного вещества, где соответственно образуется дырка. Последовательное заполнение образующихся дырок электронами эквивалентно движению дырок в полупроводнике, т. е. дырки не остаются локализованными, а перемещаются в решетке кремния как свободные положительные заряды. Избыточный же отрицательный заряд, связан с атомом примеси и по решетке перемещаться не может. 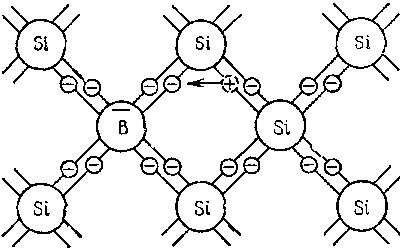 Рис. 3. Решетка кремния с примесью атомов бора. Таким образом, в полупроводниках с примесью, валентность которой на единицу меньше валентности основных атомов, носителями тока являются дырки; возникает дырочная проводимость.Полупроводники с такой проводимостью называются дырочнымиили полупроводниками р– типа. Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторами, а энергетические уровни примесей – акцепторными уровнями. В отличие от собственной проводимости, осуществляющейся одновременно электронами и дырками, примесная проводимость полупроводников обусловлена в основном носителями одного знака: Электронами – в случае донорной примеси, дырками – в случае акцепторной. Эти носители тока называются основными. Кроме основных носителей в полупроводнике имеются и неосновные носители: в полупроводниках n-типа – дырки, в полупроводниках р- типа – электроны. Контакт двух полупроводников называют p-n– переходом. P-n-переход создаётся в одном кристалле путём введения в него определенных примесей. В кристалле образуется узкая область, в которой меняется тип проводимости полупроводника от n к p. Рассмотрим кратко физические процессы, происходящие в р-n–переходе. Пусть имеются полупроводник и n- и р- типов проводимости. 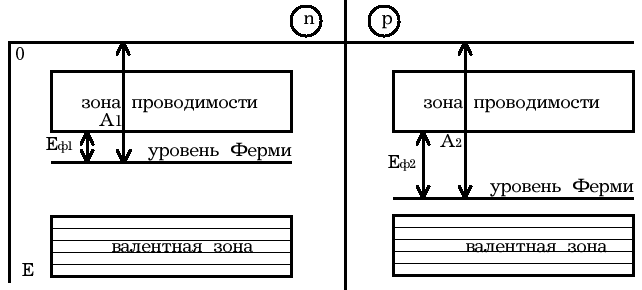 Рис.4. Уровни Ферми в донорном и акцепторном полупроводниках. Если контакт между полупроводниками р- и n- типа отсутствует, то уровни Ферми на их энергетических схемах (рис.4) расположены на разной высоте, причем в полупроводнике р- типа ближе к валентной зоне, в полупроводнике n- типа ближе к зоне проводимости (работа выхода из р- полупроводника А2 всегда превышает работу выхода из n- полупроводника А1). При возникновении контакта (рис.5) происходит обмен носителями тока, в результате которого уровни Ферми выравниваются. В приконтактной области образуется так называемый запирающий слой толщиной lp+ln обедненный основными носителями тока: электронами со стороны электронного полупроводника, дырками со стороны дырочного полупроводника. Ионы примесей этого слоя создают положительный объемный заряд в n- области и отрицательный - в р- области. Между р- и n- областями возникает контактная разность потенциалов Uк=(A2-A1)/e препятствующая движению основных носителей. Если в отсутствие освещения закоротить наружные концы двух областей p-n– перехода, то тока в цепи не будет. Это означает, что в состоянии равновесия суммарный ток, созданный движением основных и неосновных носителей через переход, равен нулю. 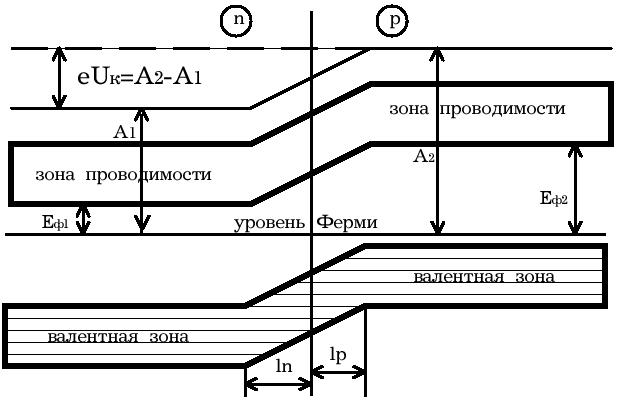 Рис.5 Энергетическая диаграмма р-n ― перехода в равновесии. Подключение к контакту внешнего напряжения прямой полярности +U (плюс со стороны р- полупроводника, минус со стороны n- полупроводника) приводит к уменьшению потенциального барьера запирающего слоя. Число основных носителей, способных пройти через p-n– переход, растет, поток неосновных носителей при этом не изменяется. Через контакт идет заметный ток в прямом направлении (рис.6, участок ОС). Если полярность внешнего напряжения изменить на противоположное (плюс со стороны n-полупроводника, минус со стороны р-полупроводника), то поле контакта увеличивается, т.е. увеличивается потенциальный барьер для основных носителей заряда. Это значит, что ток основных носителей практически равен нулю. Через р-n- переход течёт только ток неосновных носителей заряда, т. к. для них потенциального барьера нет. Это обратный ток, и он быстро достигает насыщения. В теории получено выражение для вольт-амперной характеристики р-n–перехода: где Is- ток насыщения неосвещенного р-n-перехода, k - постоянная Больцмана, е – заряд электрона, Т- абсолютная температура, знаки “плюс” и “минус” относятся соответственно к прямому и обратному направлению внешнего поля, U- внешнее напряжение. Вольт- амперная характеристика неосвещенного р-n-перехода представлена на рис. 6 (кривая 1). 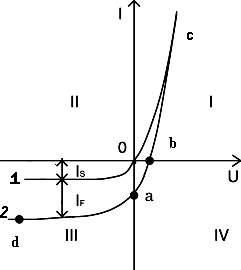 Рис. 6. Вольтамперные характеристики неосвещенного и освещенного p-n― перехода. Пусть теперь на полупроводник вблизи p-n– перехода падает свет. Концентрация электронно-дырочных пар, возникающих в результате внутреннего фотоэффекта, уменьшается по мере удаления от освещенной поверхности. В результате диффузии электроны и дырки перемещаются к переходу, где происходит их разделение: основные носители области задерживаются контактным полем, неосновные - ускоряются и свободно проходят через p-n– переход, образуя фототок Iф, текущий в обратном направлении. Если цепь разомкнута, то на границах p-n- перехода накапливается объемный заряд, препятствующий движению неосновных носителей. Возникает фото- ЭДС Uф, полярность которой обратна полярности контактной разности потенциалов. Потенциальный барьер запирающего слоя уменьшается (Рис. 7). Это в свою очередь вызывает появление так называемого тока утечки Iу, текущего в прямом направлении. Величина фото- ЭДС растет до тех пор, пока возрастающий ток основных носителей не скомпенсирует фототок. Вентильный фотоэффект заключается в возникновении фото-ЭДС на р-n–переходе при его освещении. Знак фото- ЭДС обратен знаку контактной разности потенциалов. При увеличении освещённости р-n– перехода фото- ЭДС увеличивается, но не может превысить Uk. 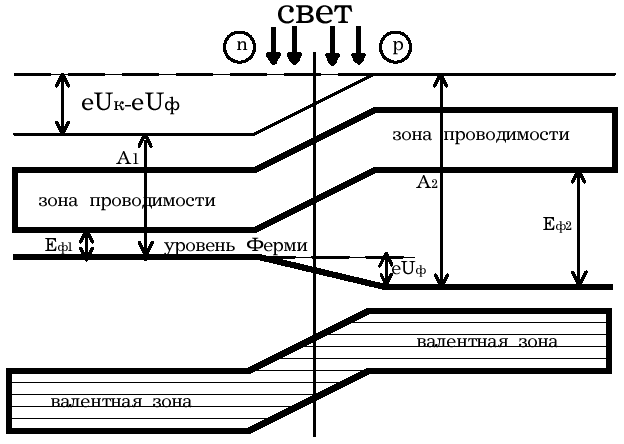 Рис.7 Энергетическая диаграмма освещенного p-n-перехода. 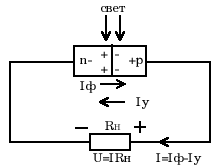 Рис.8 Освещенный p-n― переход, замкнутый на сопротивление нагрузки Rн. Замкнем p-n- переход на нагрузочное сопротивление Rн (Рис.8). Такой режим работы освещенного p-n–перехода (фотоэлемента) называется фотогальваническим. По цепи потечет ток, который можно представить как сумму двух токов: I=Iф-Iу. (2) Ток утечки Iу рассчитывается по формуле (1) для неосвещенного p-n- перехода, когда к нему приложено внешнее напряжение Uн=IRн в прямом направлении: В режиме короткого замыкания (Rн = 0) будет (Uн=0 Iу=0, ток короткого замыкания Iк.з. равен фототоку, который в свою очередь пропорционален световому потоку Ф: Iк.з.=Iф; IфФ (3) В режиме холостого хода цепь разомкнута (Rн = ), напряжение холостого хода Ux.x.=Uф I=0 Iф=Iу. Из формулы (1) следует: можно выразить Uxx: Таким образом, вентильные фотоэлементы позволяют осуществить непосредственное превращение лучистой энергии в электрическую, поэтому их также называют фотогальваническими элементами. Вольтамперная характеристика освещенного p-n–перехода представлена на рис.6 (кривая 2). Отрезок Оа (U=0) соответствует току короткого замыкания (Rн=0), отрезок Оb (I=0) - величине напряжения холостого хода (Rн=). При изменении внешней нагрузки от 0 до получаем участок ab, который и представляет собой собственно вольтамперную характеристику р-n– перехода в фотогальваническом режиме при постоянной освещенности E. Участок bc характеризует работу фотоэлемента при подаче на p-n- переход прямого внешнего напряжения, участок ad – обратного внешнего напряжения, так называемый фотодиодный режим работы. 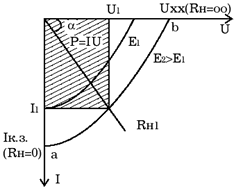 Рис. 9 Вольтамперные характеристики освещенного p-n- перехода в фотогальваническом режиме. При изменении светового потока, а следовательно, и освещенности вольтамперные характеристики смещаются, форма их изменяется. Семейство вольтамперных характеристик вентильного фотоэлемента в фотогальваническом режиме при различных освещенностях представлено на рис. 9. Прямые, проведенные из начала координат под углом , определяемым величиной сопротивления нагрузки (ctg=Rн), пересекают характеристику в точках, абсциссы которых дают падение напряжения на нагрузке, а ординаты – ток во внешней цепи, например U1=I1Rн1. Площадь, заштрихованная на рисунке, пропорциональна мощности P1, выделяемой на нагрузке Rн1: Оптимальное сопротивление нагрузки RH.ОПТ выбирается так, чтобы эта мощность была максимальной. Коэффициент полезного действия η фотогальванического элемента определяется соотношением: где - так называемая световая отдача, которая для волны длиной =555нм равна =628 лм/Вт, S – площадь приемной части фотоэлемента (в данной работе S=1,485·10-3 м2). Оборудование: Установка У-1 (источник света 1, кремниевый вентильный фотоэлемент 2 микроамперметр), магазин сопротивлений 3, милливольтметр (рис. 10). 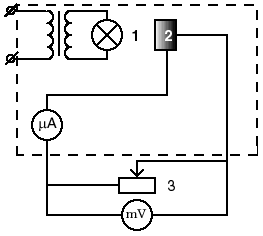 Рис. 10 Установка для изучения вентильного фотоэффекта (выделена пунктиром) и схема подключения приборов. 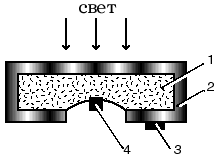 Рис. 11 Кремниевый вентильный фотоэлемент. 1 – пластинка кремния n- типа, 2 – пленка кремния p- типа, 3,4 – контакты. Кремниевый вентильный фотоэлемент (Рис. 11) представляет собой пластинку 1 кремния n- типа, вырезанную из монокристалла, на поверхности которой путем прогрева при температуре 1200С в парах BCI3 сформирована тонкая пленка 2 кремния p- типа. Контакт внешней цепи с p- областью осуществляется через металлическую полоску 3, напыленную на ее поверхности. Для создания контакта 4 с n- областью часть наружной пленки сошлифовывается Задание 1. Снятие вольтамперных характеристик кремниевого вентильного фотоэлемента. 1. Ознакомиться с устройством установки. 2. Собрать схему, представленную на рис. 10. 3. Установить r`=0 (r=r`+r0, где r – расстояние от фотоэлемента до источника света, r0= 4 см – минимальное расстояние от источника света до фотоэлемента, r` - смещение). При этом освещенность фотоэлемента будет максимальной. Изменяя сопротивление Rн от 0 до , снять значения напряжения и тока. Результаты занести в таблицу 1. Таблица 1
4. Повторить п. 3 для пяти - семи различных расстояний r=4, 6, 8см... Различные освещенности получаются путем изменения расстояния r от фотоэлемента до источника света и рассчитываются по формуле E=Iсв/r2, где Iсв - сила света источника. Iсв≈1кд.) Задание 2. Исследование вольтамперных характеристик кремниевого вентильного фотоэлемента. 1. Построить семейство вольтамперных характеристик. 2. Для каждой освещенности из соответствующей вольтамперной характеристики определить максимальную мощность фототока Pмакс и для этого случая по формуле (7) рассчитать КПД фотоэлемента (S=1,485·10-3 м2). Результаты занести в таблицу 2. Таблица 2
3. Зная Pмакс для всех освещенностей, рассчитать по формуле (6) оптимальные нагрузочные сопротивления Rн.опт. Заполнить таблицу 2. Построить график Rн.опт=f(Е) для данного вентильного фотоэлемента. 4. Занести в таблицу значения Iк.з. (при Rн=0) и Uхх (при Rн=∞). Построить графики Iк.з.=f(E); Uхх=f(E). 5. Сформулировать выводы по работе. Контрольные вопросы. Что такое полупроводники и чем они отличаются от металлов и диэлектриков? Что называется собственной проводимостью? Примесной проводимостью? Опишите явление, возникающее при контакте p- и n- полупроводников. Что такое запирающий слой? Что такое контактная разность потенциалов? Опишите p-n– переход в равновесном состоянии; при прямом включении; при обратном включении. Объясните явление возникновение фото-ЭДС при освещении p-n–перехода. Что такое фотогальванический режим работы освещённого p-n–перехода? Как снять вольтамперные и световые характеристики фотоэлемента при разных освещенностях? Как можно определить фото – ЭДС, напряжение холостого хода и ток короткого замыкания фотоэлемента? Литература. Савельев И. В. Курс общей физики т. 3 Лабораторный практикум по физике /Ахматов А. С., Андреевский В. М., Кулаков А. И. И др./- М. 1980г. Лысов В. Ф. Практикум по физике полупроводников. М. , 1976г. ЛАБОРАТОРНАЯ РАБОТА №18Изучение спектра испускания водорода. Цель работы: экспериментальное изучение серии Бальмера в спектре испускания водорода, определение постоянной Ридберга. Оборудование :стилоскоп, спектральные трубки, генератор высоковольтный школьный типа "Спектр-1", выпрямитель ВС 4-12. Краткая теория. 1.Ядерная модель атома. Опытами Резерфорда (1911 г.) было установлено, что атом любого химического элемента состоит из положительно заряженного ядра, вокруг которого расположены электроны, так что в целом атом нейтрален. Ядро, в котором сосредоточена почти вся масса атома, занимает ничтожно малую часть всего объёма. Диаметр ядра порядка 10-12 – 10-13 см при размерах атома порядка 10-8 см. Электроны вращаются вокруг ядра в первом приближении по круговым орбитам. Рассмотрим атом водорода и сходные с ним ионы (водородоподобные атомы), т.е. предположим, что имеется атомная система, состоящая из ядра с зарядом +Ze и одного электрона (Z - порядковый номер элемента в таблице Менделеева). Кулоновская сила взаимодействия между ядром и электроном является центростремительной силой: 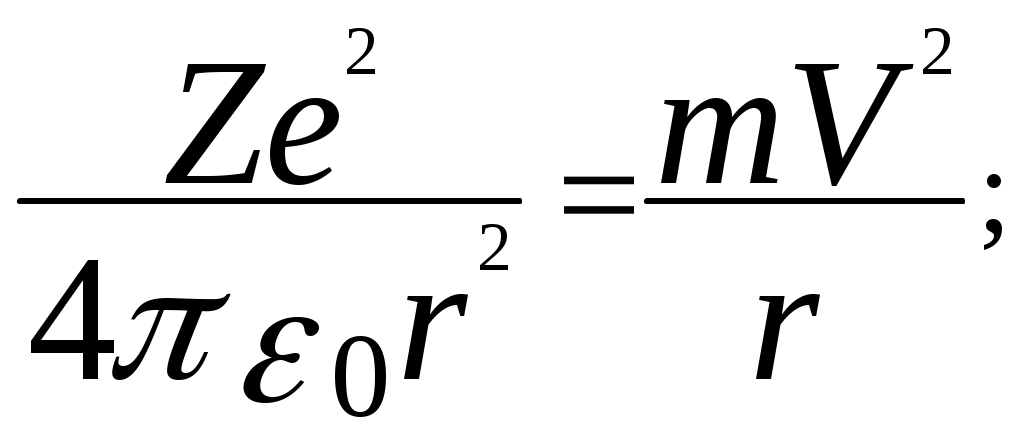 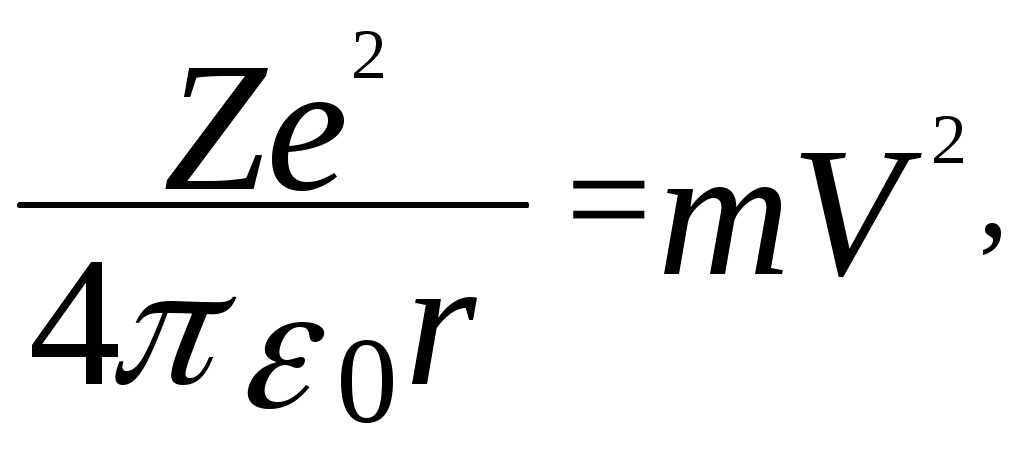 (1) (1)где m - масса электрона, г - радиус орбиты. Электрон, находящийся в электрическом поле ядра, обладает потенциальной энергией: 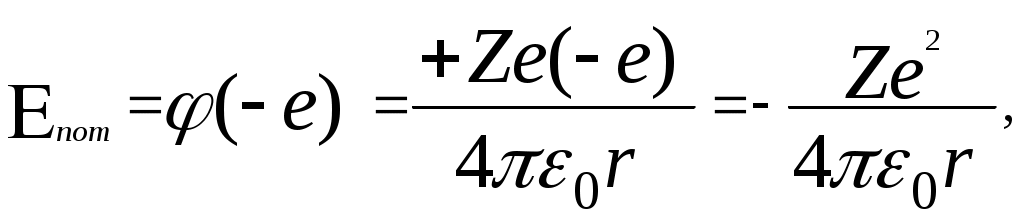 (2) (2) где 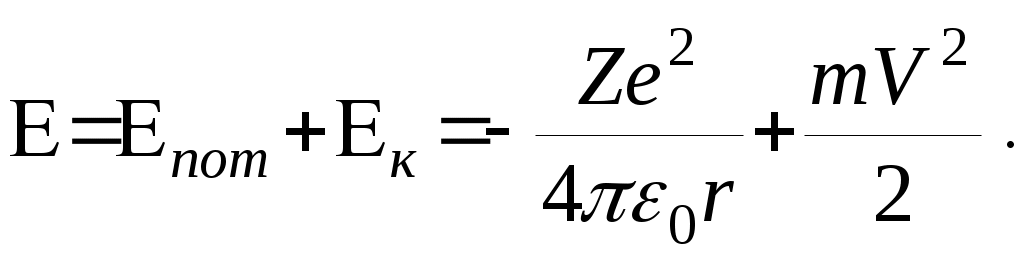 (3) (3)Из (1), (2), (3) получим: 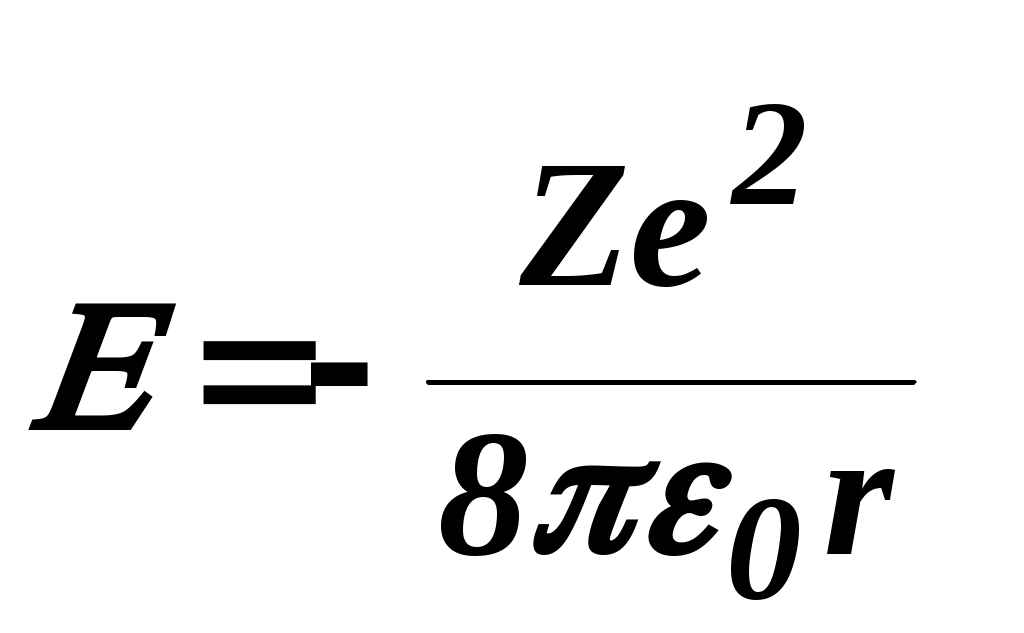 . (4) . (4)Согласно электромагнитной теории вращающийся по орбите электрон возбуждает вокруг себя переменное электромагнитное поле, распространяющееся в пространстве со скоростью света. Это означает, что вращение электрона должно вызывать непрерывное излучение, на которое электрон затрачивает часть своей энергии. Таким образом, согласно классической теории, энергия электрона всё время уменьшается. Из формулы (4) следует, что меньшему значению энергии (с учётом знака) соответствует меньший радиус. В результате электрон должен упасть на ядро. В действительности же атом является устойчивой системой. Из формулы (1) следует, что с уменьшением радиуса орбиты, скорость электрона возрастает, т.е. период обращения уменьшается. Это должно привести к непрерывному увеличению частоты излучаемых электромагнитных волн и атом должен излучать сплошной спектр. Выход из создавшегося положения был предложен Бором (1913 г.) 2.Теория Бора водородоподобных атомов. Для объяснения сериальных закономерностей в спектре испускания водорода Бор использовал гипотезу М. Планка о квантовом характере излучения и поглощения света и ядерную модель атома Резерфорда. Он сформулировал два постулата, на основе которых удалось объяснить спектр испускания атома водорода. Атомы существуют в стационарных состояниях, в которых они не излучают и не поглощают энергию. Стационарным состояниям соответствуют стационарные орбиты электрона; для этих орбит момент импульса электрона принимает определенные значения, т. е. квантуется: 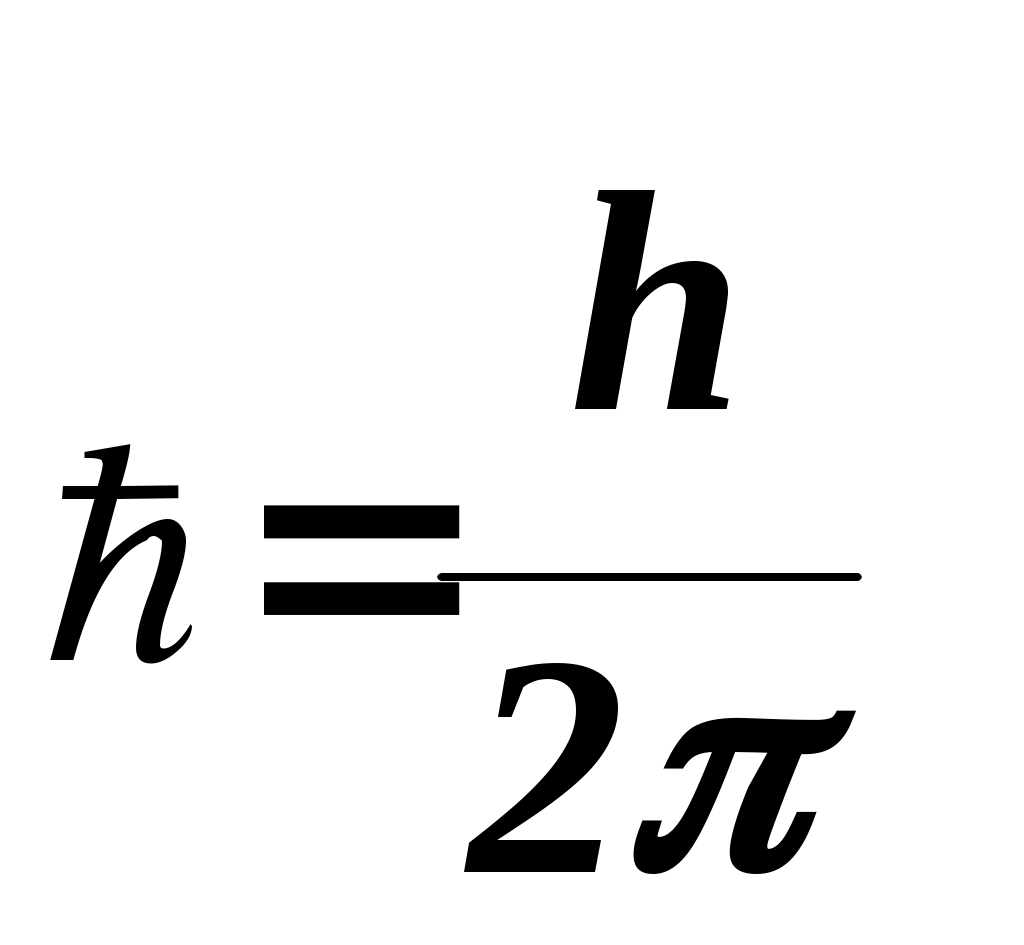 - постоянная Планка. - постоянная Планка.n- главное квантовое число, n=1,2,3… Излучение энергии происходит при переходе атома из стационарного состояния с большим значением энергии E1в состояние с меньшим значением энергииE2: Поглощение энергии имеет место когда энергия конечного состояния атома больше энергии начального состояния. Вычислим радиусы стационарных орбит и полную энергию электрона в водородоподобном атоме. Исключив V- скорость электрона из (1) и (5), получим: 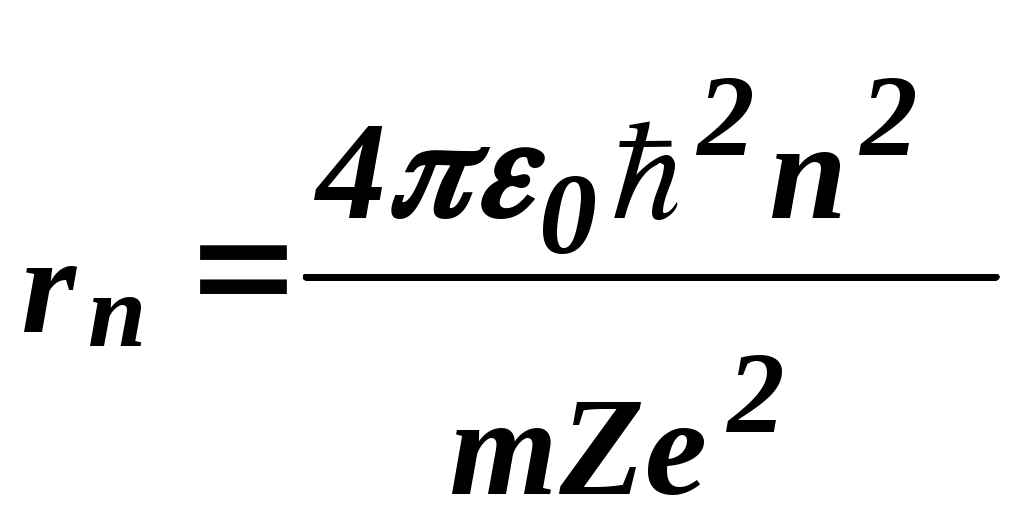 . (7) . (7)Подставим rn в (4): 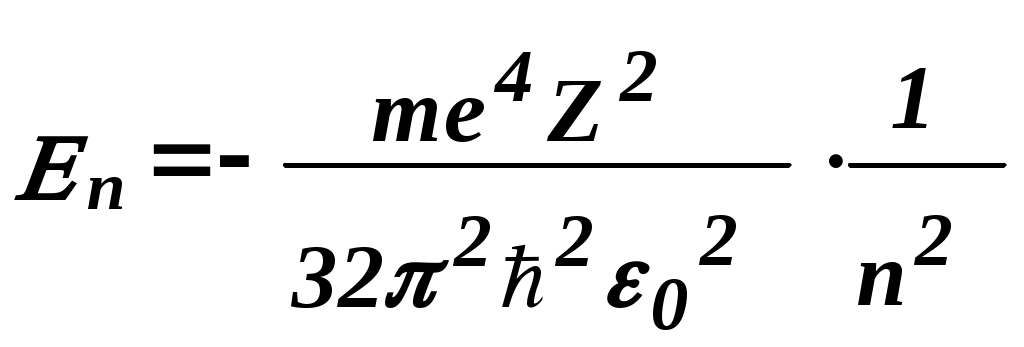 . . Для атома водорода Z=1 тогда полная энергия электрона En: 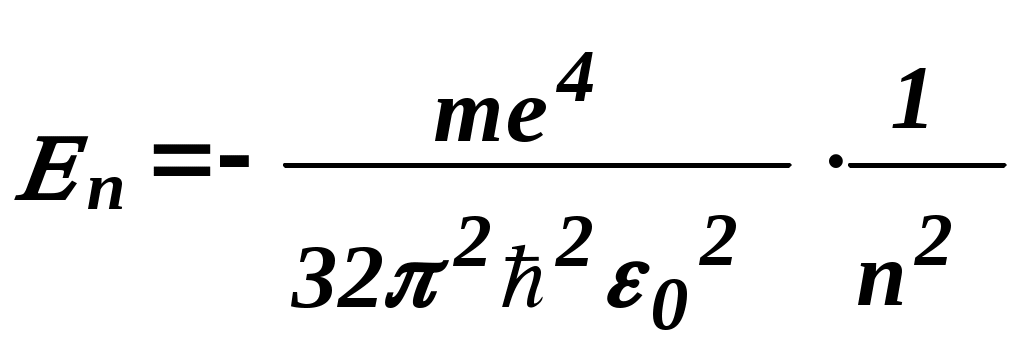 . (9) . (9)Эта формула описывает энергетический спектр электрона в атоме водорода. Согласно второму постулату Бора, при переходе из состояния с энергией Em в состояние с меньшей энергией En атом испускает квант энергии: 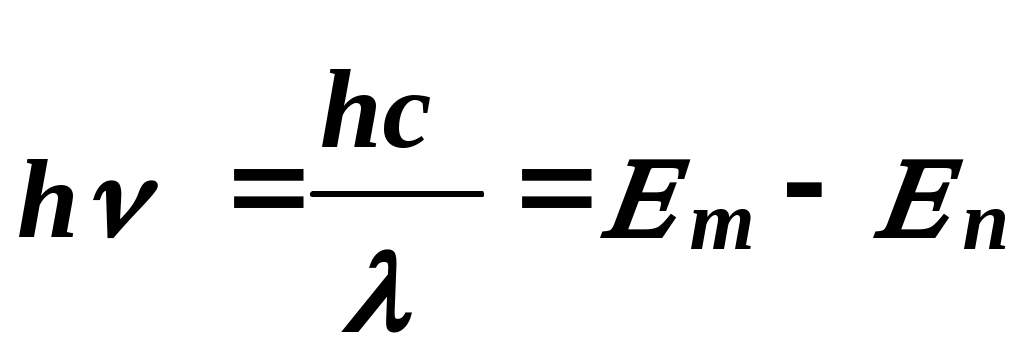 , (10) , (10)с- скорость света. Учтя (9) получим: 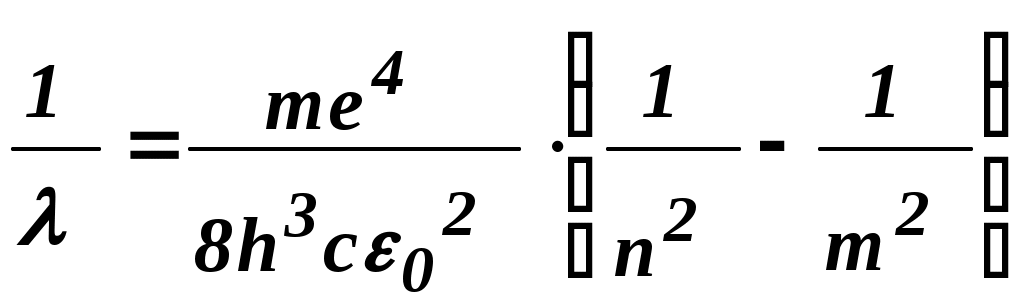 . (11) . (11)Формула (11) очень хорошо описывает спектр испускания атома водорода, а коэффициент перед скобками совпадает с величиной постоянной Ридберга R, определенной из анализа спектра испускания атома водорода: 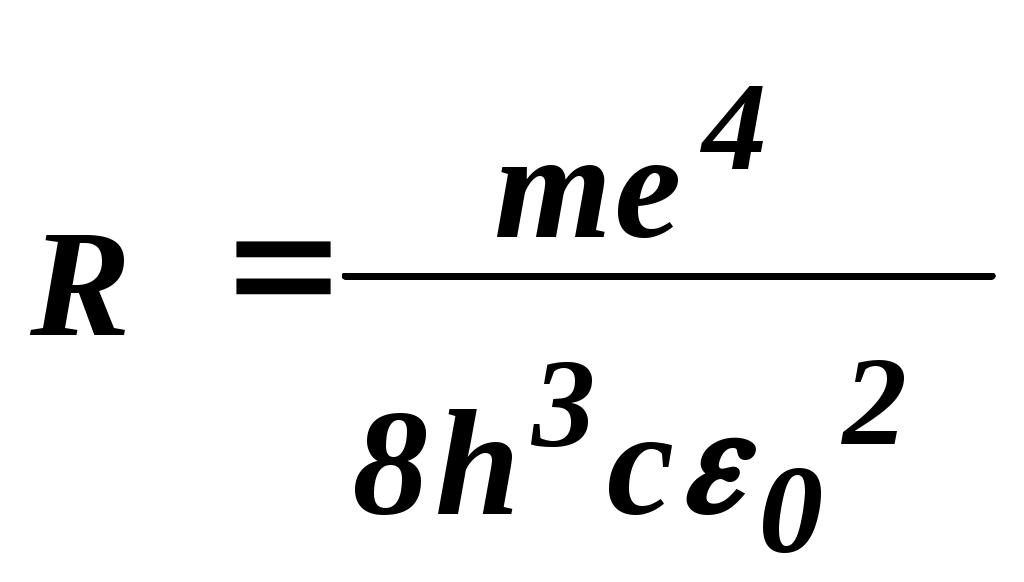 (12) (12) Серией называется совокупность линий, принадлежащих к определенному интервалу длин волн. При n=1, m=2, 3, 4…(n+1,n+2,…). образуется серия Лаймана. При n=2, m= 3, 4, 5… - серия Бальмера. При n=3, m=4, 5, 6… - серя Пашена. При n=4, m=5, 6, 7… - серия Бреккета и т. д. В данной работе изучается серия Бальмера, основные (наиболее яркие) линии которой лежат в видимой части спектра (0,4 – 0,7 мкм): Hα - красная, Hβ - голубовато-зеленая,Hγ - синяя,Hδ - фиолетовая. Несмотря на отличное объяснение спектральных закономерностей водородоподобных атомов, теория Бора обладает рядом недостатков. В частности, она не может объяснить спектры излучения более сложных атомов и различную интенсивность спектральных линий. Эти трудности были преодолены квантовой теорией, показавшей неприменимость классических представлении к микрообъектам. Задание. Включить выпрямитель ВС4-12. Установить трубку с водородом напротив входной щели стилоскопа, просмотреть спектр испускания водорода. Вращая барабан, последовательно совместить линии спектра Hα, Hβ, Hγ, Hδ c указателем в окуляре. Записать деления барабана. По градуировочному графику определить длины волн серии Бальмера. По формуле (11) рассчитать величину R и её среднее значение. По формуле (12) рассчитать массу электрона, а по формуле (7) величину r1 - первого боровского радиуса. Полученные величины R, m, r1 сравнить с табличными значениями. Градуировочной график стилоскопа прилагается к описанию работы. Контрольные вопросы. В чем состоит ядерная модель атома Резерфорда? Почему электрон, двигающийся в атоме по круговой орбите, согласно классической электродинамике должен упасть на ядро? Сформулируйте постулаты Бора. Вывести формулу (9). Вывести формулу (11). Литература. И.В. Савельев «Курс общей физики», т. 3. С.Э. Фриш, А.В. Тиморева «Курс общей физики», т. 3. «Элементарный учебник физики» под ред. Г.С. Ландсберга, т. 3. . . Градуировочный график стилоскопа. длина волны, мкм.  ЛАБОРАТОРНАЯ РАБОТА №21Изучение законов теплового излучения. Цель работы: проверить закон Стефана-Больцмана. определить постоянную Стефана-Больцмана. Оборудование: пирометр марки ОППИР-09, РНШ, понижающий трансформатор, амперметр, вольтметр, лампа накаливания с вольфрамовой спиралью, аккумулятор НКН-10, болометр, модель абсолютно черного тела, цифровой вольтметр В7-21. Краткая теория. Электромагнитное излучение любого тела, возникающее в результате теплового движения его атомов или молекул (то есть за счет его внутренней энергии), называется тепловым излучением. Характерной особенностью теплового излучения является то, что в его состав входят электромагнитные волны с длинами от 0 до , то есть его спектр является непрерывным (сплошным). Энергия излучения неодинакова для разных длин волн. Распределение излучения по длинам волн зависит от температуры излучающего тела. При низких температурах испускается, главным образом, инфракрасное излучение. При увеличении температуры возрастает интенсивность излучения, при этом в его составе увеличивается доля энергии, приходящаяся на более короткие длины волн. Задача о распределении энергии излучения нагретых тел по длинам волн сыграла существенную роль в развитии основных идей современной физики. Из опыта установлено, что если тело при данной температуре более интенсивно излучает в определенном интервале длин волн, то оно при этих же условиях лучше и поглощает излучение в этом же интервале. Иначе говоря, тела, которые лучше испускают излучение, лучше его и поглощают. Установлено также, что единственным видом излучения, способным находится в равновесии с излучающими телами, является тепловое излучение, то есть оно является равновесным. Равновесие означает, что распределение энергии между телом и излучением для каждой длины волны остается неизменным. Все остальные виды излучения, объединенные под общим названием люминесценция, является неравновесными. Для количественного описания теплового излучения введем ряд характеристик. 1. Энергетическая светимость R - поток энергии, испускаемой единицей площади поверхности излучающего тела по всем направлениям: где Ф - энергия, излучаемая телом в единицу времени по всем направлениям, S - площадь поверхности излучающего тела. 2. Испускательная способность r,т, которая определяется как: где dR - поток энергии, испускаемой единицей поверхности тела в интервале длин волн от до +d. Значит, испускательная способность показывает энергетическую светимость, приходящуюся на единичный интервал длин волн. Таким образом: Индексы и Т указывают на зависимость r,т от длины волны и температуры. 3. Поглощательная способность тела а,т определяется соотношением: где dФ - поток энергии излучения, падающий на поверхность тела, в интервале длин волн от до +d, dФ′ - поток, поглощаемый поверхностью тела в том же интервале длин волн.  Как видно из определения, а,т показывает, какая часть падающего потока dФ поглощается телом. Тело, которое при любой неразрушающей его температуре поглощает все падающее на него излучение, называется абсолютно черным телом. Для него а,т=1. Абсолютно черных тел в природе не существует. Хорошим приближением к абсолютно черному телу является полость с отверстием (рис.1). Как видно из определения, а,т показывает, какая часть падающего потока dФ поглощается телом. Тело, которое при любой неразрушающей его температуре поглощает все падающее на него излучение, называется абсолютно черным телом. Для него а,т=1. Абсолютно черных тел в природе не существует. Хорошим приближением к абсолютно черному телу является полость с отверстием (рис.1).При каждом акте отражения излучения от стенок полости часть энергии поглощается. В результате многократных отражений практически все излучение будет поглощено. Тело, для которого а,т=const<l, называется серым телом. В 1859 году немецкий физик Кирхгоф на основании второго начала термодинамики установил один из законов теплового излучения, который впоследствии был подтвержден экспериментально. Согласно закону Кирхгофа, отношение испускательной способности тела к его поглощательной способности не зависит от природы тела и является универсальной функцией длины волны и температуры: где индексы 1, 2, ..., n - номер тела. В общем виде: Из закона Кирхгофа следует, что для абсолютно черного тела (а,т =l) и (r,т)абс.ч.т. = f(,Т) Универсальная функция в законе Кирхгофа и есть испускательная способность абсолютно черного тела. Поиски вида этой функции привели к возникновению квантовых представлений о природе излучения. В 1884 году Л. Больцман теоретически доказал, что энергетическая светимость абсолютно черного тела пропорциональна четвертой степени его абсолютной температуры: 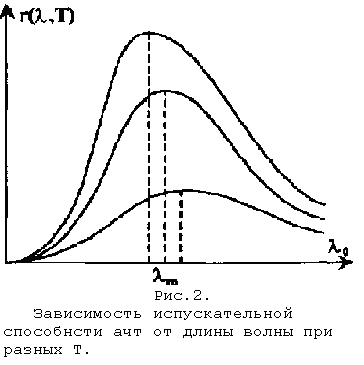 R=T4. (6) Экспериментально он был установлен в 1879 году Стефаном. Этот закон (6) называется законом Стефана-Больцмана. - постоянная Стефана-Больцмана. = 5,6710-8 Распределение энергии излучения абсолютно черного тела (ачт) было тщательно изучено на опыте (рис.2). Анализ этих кривых показывает, что для каждой температуры существует такая длина волны т, вблизи которой излучается наибольшая часть энергии абсолютно черного тела. С ростом температуры длина волны т уменьшается. Вин установил, что длина волны, на которую приходится максимум испускательной способности абсолютно черного тела, обратно пропорциональна абсолютной температуре тела: Это закон смещения Вина. b - постоянная Вина. b = 2,9 10-3 м К. Все попытки теоретически найти вид такой функции f(,T), который бы совпал с опытными результатами (рис.2) терпели неудачу. Выход из тупика нашел Планк (1900 г.), который предположил, что энергия излучается и поглощается порциями (то есть дискретно), которые называются квантами. Энергия кванта: где - частота излучения, h - постоянная Планка: h =6,63 10 –34 Дж с. Планк вывел формулу для испускательной способности абсолютно черного тела, которая носит его имя: 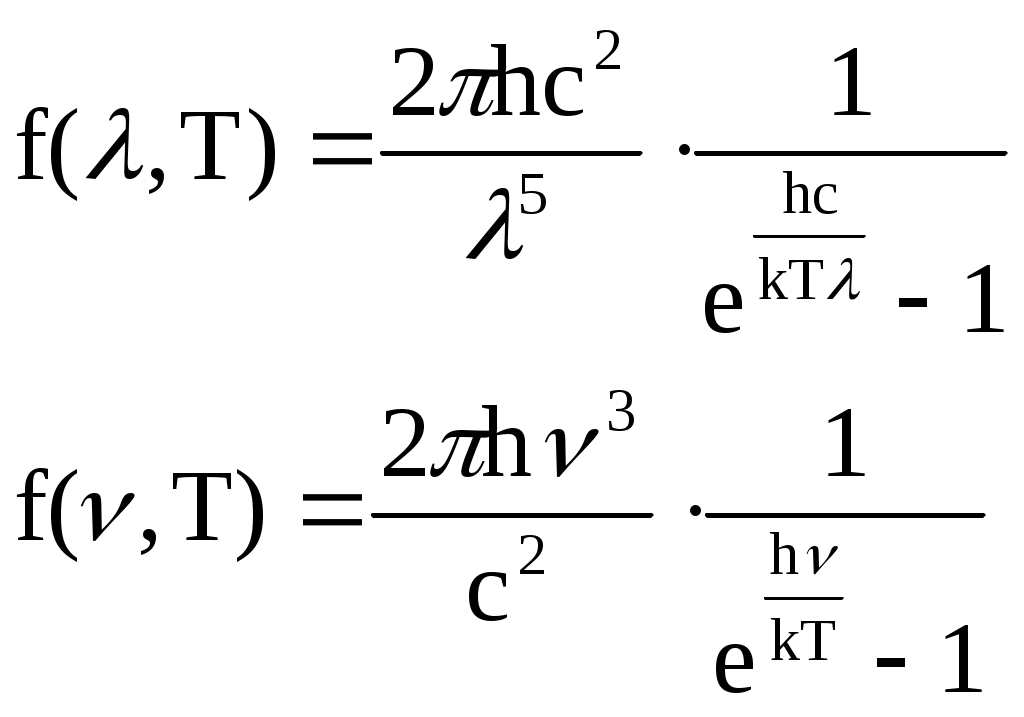 (8) Из формулы Планка вытекают законы Стефана-Больцмана и Вина. В частности, проинтегрировав формулу (8) по всем длинам волн (или частот), можно получить: (9) что очень хорошо согласуется с экспериментальным значением . Целью данной работы является проверка закона Стефана-Больцмана и определение постоянной Стефана-Больцмана. Задание 1. |
