ЛАБОРАТОРНЫЕ РАБОТЫ ПО АТОМНОЙ И КВАНТОВОЙ ФИЗИКЕ. Практикум по физике (атомная и квантовая физика) Направление подготовки 010700 (510400) Физика
 Скачать 2.87 Mb.
|
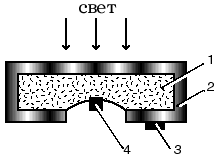
1200°С в парах BCI3 сформирована тонкая пленка 2 кремния p- типа. Контакт внешней цепи с p- областью осуществляется через металлическую полоску 3, напыленную на ее поверхность. Для создания контакта 4 с n- областью часть наружной пленки сошлифовывается. М |
Российской Федерации
Федеральное государственное
бюджетное образовательное учреждение
высшего профессионального образования
«Курский государственный университет»
Кафедра общей физики
Лабораторный практикум по физике
(атомная и квантовая физика)
Направление подготовки 010700 (510400) Физика
Степень (квалификация) Бакалавр физики
Профиль подготовки Физика конденсированного состояния
Физико-математический факультет
Очная форма обучения
Курск 2012
ЛАБОРАТОРНАЯ РАБОТА №7
Изучение вентильного фотоэффекта
Цель работы: ознакомление с вентильным фотоэффектом, исследование вольтамперных характеристик вентильного фотоэлемента.
Оборудование: 1. Источник света: лампа накаливания, U=3В, Iсв=1 кд.
2. Кремниевый фотоэлемент, площадь приемной части S=1,485·10-3 м2.
3. Магазин сопротивления Р-33 (0¸99999) Ом.
4. Трансформатор.
5. Микроамперметр: предел измерений 100мкА.
6. Цифровой вольтметр Щ - 300.
7. Линейка.
Краткая теория
Наиболее отчетливо полупроводники отличаются от проводников характером зависимости электропроводимости от температуры. Измерения показывают, что у полупроводников удельное сопротивление с увеличением температуры не растет, как у металлов, а, наоборот, чрезвычайно резко уменьшается. При температурах, близких к абсолютному нулю, удельное сопротивление полупроводников очень велико. Это означает, что при низких температурах полупроводник ведет себя как диэлектрик.
Кремний – четырехвалентный элемент. Это означает, что во внешней оболочке атома имеются четыре электрона, сравнительно слабо связанные с ядром. Взаимодействие пары соседних атомов осуществляется с помощью парной электронной связи, называемой ковалентной связью. Каждый атом образует четыре связи с соседними, и любой валентный электрон может двигаться от одного атома к соседнему, дойдя до соседнего он может перейти к следующему, при этом, электрон не является свободным и прочно «привязан» к кристаллической решетке, и внешнее электрическое поле не оказывает заметного влияния на его движение.
При нагревании кристалла кинетическая энергия валентных электронов повышается, и наступает разрыв отдельных связей. Некоторые электроны становятся свободными, подобно электронам в металле.
П
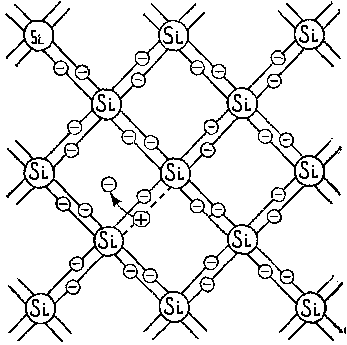ри разрыве ковалентной связи образуется вакантное место недостающего электрона. Его называют дыркой. Дырка имеет избыточный положительный заряд (рис.1). Положение дырки в кристалле не является неизменным. Непрерывно происходит следующий процесс. Один из электронов, обеспечивающих связь атомов, перескакивает на место образовавшейся дырки и восстанавливает здесь электронную связь, а там, откуда перескочил этот электрон, образуется новая дырка. Таким образом, дырка может перемещаться по всему кристаллу в направлении противоположном движению электрона. Движение электронов и дырок в отсутствие электрического поля является хаотическим. В полупроводниках наряду с процессом генерации электронов и дырок идет процесс рекомбинации(исчезновение свободной пары электрон – дырка): электроны переходят из зоны проводимости в валентную зону, отдавая энергию решетке.Рис. 1 Условная схема кристалла кремния.
Электронно-дырочная проводимость получила название собственнойпроводимости.Собственная проводимость полупроводников обычно невелика, так как мало число свободных электронов. Существенная особенность полупроводников состоит в том, что в них при наличии примесей наряду с собственной проводимостью возникает примесная проводимость.
Примесная проводимость полупроводников обусловлена наличием посторонних атомов в кристаллической решётке, а также определяется количеством и типами различных дефектов структуры кристалла.
Наличие в полупроводнике примеси существенно изменяет его проводимость. Например, при введении в кремний примерно 0,001ат. % бора его проводимость увеличивается примерно в 106 раз.
Примесную проводимость полупроводников рассмотрим на примере Si, в который вводятся атомы с валентностью, отличной от валентности основных атомов на единицу. Например, при замещении атома кремния пятивалентным атомом мышьяка (рис. 2) один электрон не может образовать ковалентной связи, он оказывается «лишним» и может легко покинуть атом, т. е. стать свободным.
Образование свободного электрона не сопровождается нарушением ковалентной связи; следовательно, дырка не возникает. Избыточный положительный заряд, возникающий вблизи атома примеси, связан с атомом примеси и поэтому перемещаться по решетке не может.
Таким образом, в полупроводниках с примесью, валентность которой на единицу больше валентности основных атомов, носителями тока являются электроны; возникает электронная примесная проводимость. Полупроводники с такой проводимостью называются электроннымиили полупроводниками n-типа. Примеси, являющиеся источниками электронов, называются донорами.
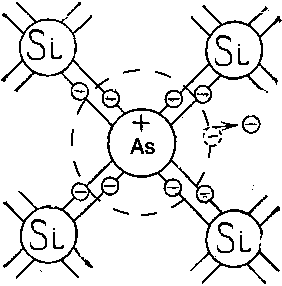
Рис. 2 Решетка кремния с примесью атомов мышьяка
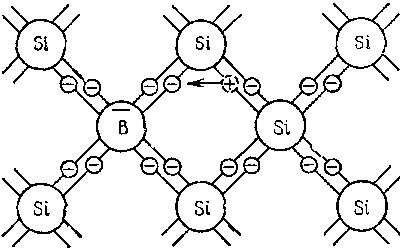Если предположить, что в решетку кремния введен примесный атом с тремя валентными электронами, например бор (рис. 3), то для образования связей с четырьмя ближайшими соседями у атома бора не хватает одного электрона, одна из связей остается неукомплектованной и четвертый электрон может быть захвачен от соседнего атома основного вещества, где соответственно образуется дырка. Последовательное заполнение образующихся дырок электронами эквивалентно движению дырок в полупроводнике, т. е. дырки не остаются локализованными, а перемещаются в решетке кремния как свободные положительные заряды. Избыточный же отрицательный заряд, связан с атомом примеси и по решетке перемещаться не может.Рис. 3 Решетка кремния с примесью атомов бора
Таким образом, в полупроводниках с примесью, валентность которой на единицу меньше валентности основных атомов, носителями тока являются дырки; возникает дырочная проводимость.Полупроводники с такой проводимостью называются дырочнымиили полупроводниками р– типа. Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторами, а энергетические уровни примесей – акцепторными уровнями.
В отличие от собственной проводимости, осуществляющейся одновременно электронами и дырками, примесная проводимость полупроводников обусловлена в основном носителями одного знака: Электронами – в случае донорной примеси, дырками – в случае акцепторной. Эти носители тока называются основными. Кроме основных носителей в полупроводнике имеются и неосновные носители: в полупроводниках n-типа – дырки, в полупроводниках р- типа – электроны.
Контакт двух полупроводников называют p-n– переходом.
P-n-переход создаётся в одном кристалле путём введения в него определенных примесей. В кристалле образуется узкая область, в которой меняется тип проводимости полупроводника от n к p.
Рассмотрим кратко физические процессы, происходящие в р-n–переходе. Пусть имеются полупроводники n- и р- типов проводимости.
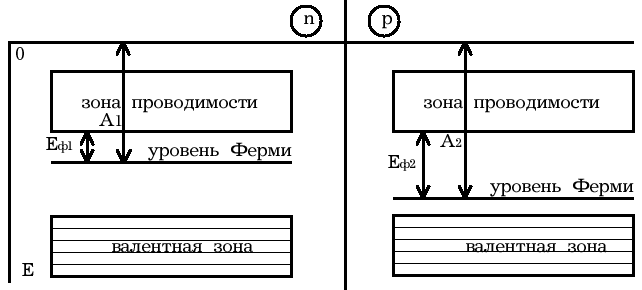
Рис.4 Уровни Ферми в донорном и акцепторном полупроводниках
Если контакт между полупроводниками р- и n- типа отсутствует, то уровни Ферми на их энергетических схемах (рис.4) расположены на разной высоте, причем в полупроводнике р- типа ближе к валентной зоне, в полупроводнике n- типа ближе к зоне проводимости (работа выхода из р- полупроводника А2 всегда превышает работу выхода из n- полупроводника А1).
При возникновении контакта (рис.5) происходит обмен носителями тока, в результате которого уровни Ферми выравниваются. В приконтактной области образуется так называемый запирающий слой толщиной lp+ln обедненный основными носителями тока: электронами со стороны электронного полупроводника, дырками со стороны дырочного полупроводника. Ионы примесей этого слоя создают положительный объемный заряд в n- области и отрицательный - в р- области. Между р- и n- областями возникает контактная разность потенциалов Uк=(A2-A1)/e препятствующая движению основных носителей.
Если в отсутствие освещения закоротить наружные концы двух областей p-n– перехода, то тока в цепи не будет. Это означает, что в состоянии равновесия суммарный ток, созданный движением основных и неосновных носителей через переход, равен нулю.
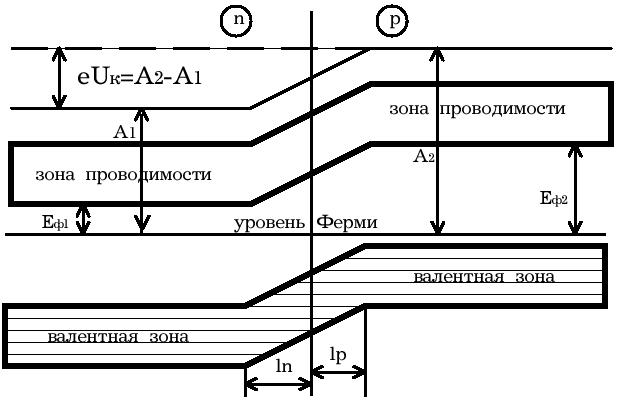
Рис.5 Энергетическая диаграмма р-n ― перехода в равновесии
Подключение к контакту внешнего напряжения прямой полярности +U (плюс со стороны р- полупроводника, минус со стороны n- полупроводника) приводит к уменьшению потенциального барьера запирающего слоя. Число основных носителей, способных пройти через p-n– переход, растет, поток неосновных носителей при этом не изменяется. Через контакт идет заметный ток в прямом направлении (рис.6, участок ОС).
Если полярность внешнего напряжения изменить на противоположное (плюс со стороны n-полупроводника, минус со стороны р-полупроводника), то поле контакта увеличивается, т.е. увеличивается потенциальный барьер для основных носителей заряда. Это значит, что ток основных носителей практически равен нулю. Через р-n- переход течёт только ток неосновных носителей заряда, т. к. для них потенциального барьера нет. Это обратный ток, и он быстро достигает насыщения.
В теории получено выражение для вольтамперной характеристики р-n–перехода:
(1)
где Is- ток насыщения неосвещенного р-n-перехода, k- постоянная Больцмана, е– заряд электрона, Т- абсолютная температура, знаки “плюс” и “минус” относятся соответственно к прямому и обратному направлению внешнего поля, U- внешнее напряжение.
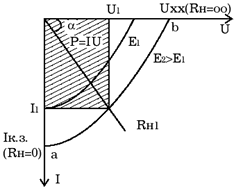
Вольтамперная характеристика неосвещенного р-n-перехода представлена на рис. 6 (кривая 1).
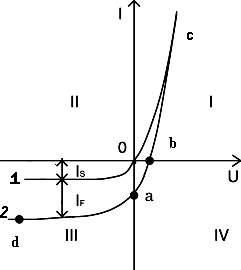
Рис. 6 Вольтамперные характеристики неосвещенного и освещенного
р-n-перехода
Пусть теперь на полупроводник вблизи p-n– перехода падает свет. Концентрация электронно-дырочных пар, возникающих в результате внутреннего фотоэффекта, уменьшается по мере удаления от освещенной поверхности. В результате диффузии электроны и дырки перемещаются к переходу, где происходит их разделение: основные носители области задерживаются контактным полем, неосновные - ускоряются и свободно проходят через p-n– переход, образуя фототок Iф, текущий в обратном направлении.
Если цепь разомкнута, то на границах p-n- перехода накапливается объемный заряд, препятствующий движению неосновных носителей. Возникает фото- ЭДС Uф, полярность которой обратна полярности контактной разности потенциалов. Потенциальный барьер запирающего слоя уменьшается (Рис. 7). Это в свою очередь вызывает появление так называемого тока утечки Iу, текущего в прямом направлении. Величина фото- ЭДС растет до тех пор, пока возрастающий ток основных носителей не скомпенсирует фототок.
Вентильный фотоэффект заключается в возникновении фото-ЭДС на р-n–переходе при его освещении. Знак фото-ЭДС обратен знаку контактной разности потенциалов. При увеличении освещённости р-n–перехода фото- ЭДС увеличивается, но не может превысить Uk.
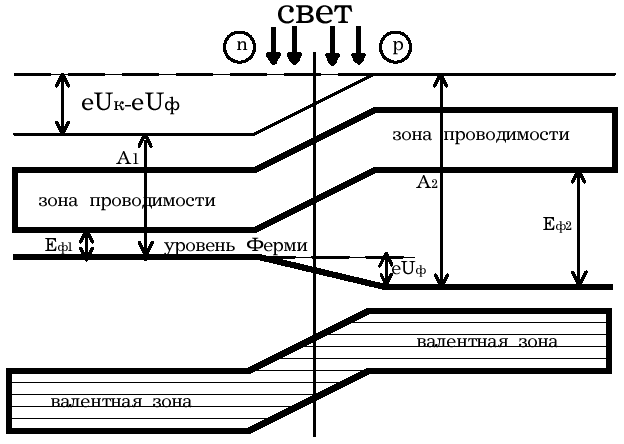
Рис.7 Энергетическая диаграмма освещенного p-n-перехода
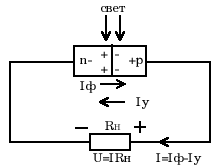
Рис.8 Освещенный p-n― переход, замкнутый на сопротивление
нагрузки Rн.
Замкнем p-n- переход на нагрузочное сопротивление Rн (Рис.8).
Такой режим работы освещенного p-n–перехода (фотоэлемента) называется фотогальваническим.
П
о цепи потечет ток, который можно представить как сумму двух токов: (2)
Т
ок утечки Iурассчитывается по формуле (1) для неосвещенного p-n- перехода, когда к нему приложено внешнее напряжение Uн=IRн в прямом направлении:В режиме короткого замыкания (Rн = 0) будет (Uн=0 Iу=0), ток короткого замыкания Iк.з. равен фототоку, который в свою очередь пропорционален световому потоку Ф:
Iк.з.=Iф; Iф
ткуда можно выразить Uxx: 
(6)
оэффициент полезного действия η фотогальванического элемента h определяется соотношением:
| r, см | I, мкА | U, В | R, Ом |
| | | | |
4. Повторить п. 3 для пяти - семи различных расстояний r=4, 6, 8см... Различные освещенности получаются путем изменения расстояния r от фотоэлемента до источника света и рассчитываются по формуле E=Iсв/r2, где Iсв - сила света источника. Iсв≈1кд.)
Задание 2. Исследование вольтамперных характеристик кремниевого вентильного фотоэлемента.
1. Построить семейство вольтамперных характеристик.
2. Для каждой освещенности из соответствующей вольтамперной характеристики определить максимальную мощность фототока Pмакс и для этого случая по формуле (7) рассчитать КПД фотоэлемента. Результаты занести в таблицу 2.
Таблица 2
| r, см | E, Лк | I1, мкА | U1, В | Pмакс, Вт | КПД | Rн,опт,, Ом | Iк,з, мкА | Uхх, В |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
3. Зная Pмакс для всех освещенностей, рассчитать по формуле (6) оптимальные нагрузочные сопротивления Rн.опт. Заполнить таблицу 2.
Построить график Rн.опт=f(Е) для данного вентильного фотоэлемента.
4. Занести в таблицу значения Iк.з. (при Rн=0) и Uхх (при Rн=∞). Построить графики Iк.з.=f(E); Uхх=f(E).
5. Сформулировать выводы по работе.
Контрольные вопросы
Что такое полупроводники и чем они отличаются от металлов и диэлектриков?
Что называется собственной проводимостью? Примесной проводимостью?
Объясните явления, возникающее при контакте p- и n- полупроводников. Что такое запирающий слой? Что такое контактная разность потенциалов?
Опишите p-n– переход в равновесном состоянии; при прямом включении; при обратном включении.
Объясните явление возникновение фото-ЭДС при освещении p-n–перехода.
Что такое фотогальванический режим работы освещённого p-n–перехода?
Как снять вольтамперные и световые характеристики фотоэлемента при разных освещенностях?
Как можно определить фото – ЭДС, напряжение холостого хода и ток короткого замыкания фотоэлемента?
Рекомендуемый список литературы
1. Савельев И.В. Курс общей физики: Учеб.: В 3т.Т3.– М.: Наука, 1987.–304с.
2. Лабораторный практикум по физике: Учеб.пособие для студентов втузов/Ахматов А.С.,Андреевский В.М.,Кулаков А.И. и др.; Под.ред. А.С.Ахматова. – М.: Высшая школа, 1980. – 360с.
3. Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Курс общей физики. Оптика и атомная физика.– М.: Просвещение. 1992.–320 с.
ЛАБОРАТОРНАЯ РАБОТА №8
Изучение счетчика Гейгера-Мюллера
Цель работы:экспериментальное измерение счетной характеристики счетчика Гейгера-Мюллера и определение мертвого времени счетчика.
Оборудование:прибор «Арион» со свинцовым домиком (рис 6), два источника β - излучения.
Краткая теория
К
Рис. 1 Торцевой (1) и цилиндрический (2) счетчики Гейгера – Мюллера
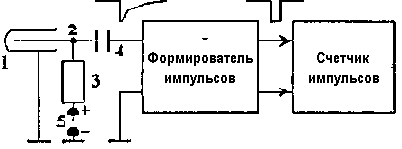
Рис. 2 Схема включения счетчика Гейгера – Мюллера. 1 – катод, 2 – анод, 3 – резистор нагрузки, 4 - разделительный конденсатор, 5 - источник питания
онструктивно газоразрядный счётчик представляет собой тонкостенную металлическую или стеклянную, покрытую с внутренней стороны слоем металла, цилиндрическую камеру (рис. 1). Цилиндр служит катодом. Анодом является тонкая (0,05…0,5 мм) металлическая нить, расположенная по оси цилиндра. Счётчик заполнен специально подобранным газом, например аргоном, при давлении 10…760 мм рт. ст. Между катодом и анодом за счёт внешнего источника, создаётся разность потенциалов 300-2500 В.
Традиционная схема включения счётчика в электрическую цепь показана на рисунке 2.
Р
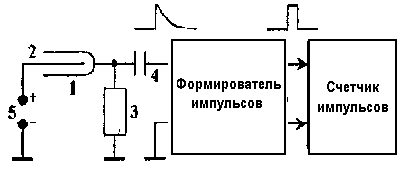
Рис. 3 Схема включения счетчика Гейгера – Мюллера в приборе «Арион». Обозначения на рис. 2
егистрируемая частица, проходящая через объём счётчика, создаёт на выходе схемы электрический импульс отрицательной полярности, так как уменьшение сопротивления самого счётчика в момент газового разряда, вызванного частицей, резко увеличивает напряжение на сопротивлении нагрузки.
В комплекте приборов «Арион» применена схема, формирующая импульс положительной полярности (рис. 3). Недостатком этой схемы является незаземлённость катода, однако, он создаёт условия для более стабильной работы счётчика импульсов.
Физические процессы, происходящие в газоразрядных счётчиках, можно разделить на три стадии.