ЛАБОРАТОРНЫЕ РАБОТЫ ПО АТОМНОЙ И КВАНТОВОЙ ФИЗИКЕ. Практикум по физике (атомная и квантовая физика) Направление подготовки 010700 (510400) Физика
 Скачать 2.87 Mb. Скачать 2.87 Mb.
|
Краткая теория .Твердые тела, независимо от их строения, способны под воздействием электрического поля проводить электрический ток. Физическая величина, количественно характеризующая эту способность называется удельной электропроводностью σ Иногда для характеристики электропровод ности веществ пользуются величиной ρ=1/σ и называемой удельным сопротивлением. В зависимости от величины ρ все вещества делятся на проводники, диэлектрики и полупроводники – вещества с промежуточными значениями ρ. Это деление является условным, т.к. электропроводность веществ меняется при изменении температуры, агрегатного состояния и зависит от других внешних воздействий, например, наличия магнитных и электрических полей, облучения и т.д. Опыт показывает, что характер зависимости электропроводности от температуры различен для разных веществ. У металлов, например, с ростом температуры электропроводность уменьшается, т.е. сопротивление увеличивается. У полупроводников наоборот, с ростом температуры электропроводность увеличивается. При очень низких температурах полупроводники ведут себя как диэлектрики. Различие в электрических свойствах проводников, диэлектриков и полупроводников удалось объяснить с единой точки зрения – на основе зонной теориитвердого тела. Электроны в изолированном атоме могут, как известно, находится лишь на определенных энергетических уровнях. При образовании твердого тела из изолированных атомов они при сближении начинают влиять друг на друга. Результатом этого взаимного влияния является расщепление энергетических уровней электронов, т.е. из одного энергетического уровня, одинакового для всех изолированных атомов в кристалле возникает набор очень близко расположенных энергетических уровней. Эти чрезвычайно близко расположенные друг к другу уровни образуют зону разрешенных значений энергии. Важно, что число уровней в зоне конечно и равно числу атомов в кристалле. Расстояние же между уровнями в зоне порядка 10 –22 эВ, т.е. энергия электрона в зоне изменяется практически непрерывно. В твердом теле существует не одна, а несколько разрешенных энергетических зон, образованных из дискретных уровней изолированных атомов. Ширина этих зон (по энергии) различна. Зоны разрешенных значений энергий разделены интервалами запрещенных значений энергии – запрещенными зонами. Таким образом, в любом кристаллическом твердом теле реализуется зонная структура, т.е. существует зонный энергетический спектр, схематически изображенный на рис.1. 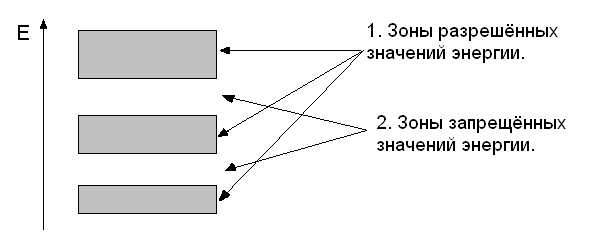 Рис. 1. Зонный энергетический спектр электронов в кристалле. Вышеизложенное следует из решения уравнения Шредингера для движения электрона в периодическом поле кристаллической решетки. Распределение электронов по энергетическим уровням разрешенных зон подчиняется принципу Паули, согласно которому в каждом энергетическом состоянии не может быть более двух электронов с антипараллельными спинами. Электрические и ряд других свойств кристаллов определяются заполнением электронами зоны, которая образовалась из расщепления того энергетического уровня изолированного атома, который соответствовал валентным электронам в основном состоянии. Эта зона называется валентной зоной (ВЗ). Выше по энергии расположена зона проводимости (ЗП). Эта зона образована из энергетического уровня возбужденного состояния изолированного атома. В зависимости от степени заполнения электронами валентной зоны и энергетического зазора ∆E между валентной зоной и зоной проводимости, твердые тела являются или проводниками, или диэлектриками, или полупроводниками. У проводников валентная зона частично заполнена электронами, поэтому эта зона в проводниках является и зоной проводимости. Другими словами, под действием электрического поля электроны могут увеличивать свою энергию (есть свободные энергетические состояния в зоне!), т.е. они являются свободными. Это случай металлов. В металлах также реализуется случай, когда полностью заполненная валентная зона частично перекрывается с зоной проводимости (рис.2а). В диэлектриках валентная зона полностью заполнена электронами (она образовалась из полностью заполненного энергетического уровня основного состояния изолированного атома) и отделена от зоны проводимости достаточно широкой запрещенной зоной ∆E>3-4 эВ (рис.2б). Т.е. в диэлектрике нет, вообще говоря, свободных носителей заряда и они обладают крайне малой электропроводностью. В полупроводниках ширина запрещенной зоны ∆E < 3 эВ (рис.2в). При Т > 0 небольшое число электронов могут за счет теплового возбуждения перейти в зону проводимости, т.е. стать свободными. В валентной зоне при этом образуется такое же количество свободных состояний, которые называются дырками. Тогда под действием электрического поля электроны в зоне проводимости будут увеличивать свою энергию и будут увеличивать свою энергию дырки. (Дырка во внешнем поле ведет себя как частица с положительным зарядом |е|.) В этом случае электропроводность полупроводника будет определяться электронами и дырками. 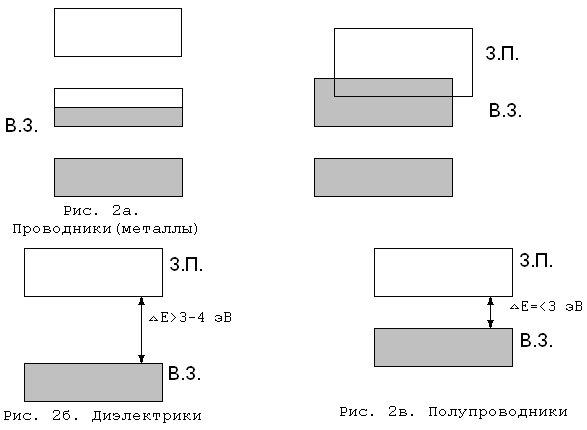 Проводимость химически чистых полупроводников называется собственной проводимостью, такие полупроводники - собственными. Примеры: химически чистые Ge, Si, GaAs, InP и т.д. Ясно, что в собственных полупроводниках концентрации электронов и дырок одинаковы.. С увеличением температуры растет концентрация электронов в зоне проводимости и дырок в валентной зоне, т.е. увеличивается электропроводимость полупроводника. В реальных кристаллах равенство концентраций электронов и дырок может нарушаться за счет атомов примесей и дефектов кристаллической решетки. Если в полупроводнике имеются атомы примеси, то в запрещенной появляются энергетические уровни двух видов (рис.3). 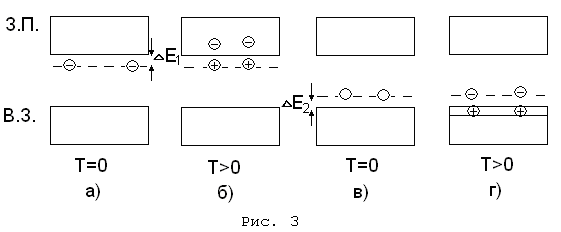 Зонный энергетический спектр полупроводника с донорной примесью а,б) и с акцепторной примесью в,г) Примесные уровни, в зависимости от валентности атомов примеси, при абсолютном нуле температуры окажутся либо заполненными (рис.За), либо незаполненными (рис.3в). Примесные уровни расположены, как правило, вблизи дна зоны проводимости и потолка валентной зоны. При Т > 0 (рис.Зв) в зоне проводимости появляются электроны, вследствие термической ионизации атомов примеси, и в этом случае проводимость полупроводника будет электронной, полупроводникназывается полупроводником n-типа, примесь называется донорной. Во втором случае (рис.Зг) при Т > 0 электроны из валентной зоны вследствие термического возбуждения будут захвачены атомами примеси и проводимость полупроводника будет дырочной.Это полупроводник р-типа. Примесь в этом случае называется акцепторной. Проводимость полупроводников в этих случаях называется примесной. При увеличении температуры из-за теплового возбуждения может оказаться, что все атомы примеси (рис.Зб) отдадут электроны в зону проводимости и электропроводность полупроводника будет примерно постоянной. (Область истощения примеси.) При дальнейшем возрастании температуры начнутся переходы электронов из валентной зоны в зону проводимости, т.е. будет иметь место переход к собственной проводимости. Таким образом, тип проводимости полупроводника зависит от концентрации примесей, температуры, подвижностей электронов и дырок. Электропроводность полупроводника в общем случае складывается из примесной и собственной. Для случая наличия только донорной примеси выражение для удельной электропроводности, в общем, можно записать: 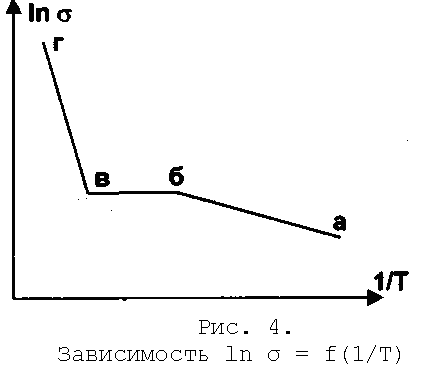 где k - постоянная Больцмана, Т - абсолютная темпера тура, ∆E-ширина запрещенной зоны, ∆E1 -энергия ионизации атомов донорной примеси. Первое слагаемое (1) характеризует примесную проводимость, а второе – собственную. В теории показано, что коэффициенты А и В слабо зависят от температуры по сравнению с экспоненциальными множителями, и мы будем считать их постоянными. Для примесного полупроводника, например, n-типа с определенной концентрацией примеси опыт дает следующую зависимость электропроводности от температуры (рис.4). Область низких температур (а-б) описывается первым слагаемым формулы (1). Область истощения примеси б-в (все примесные атомы ионизированы). Область в - г – область собственной проводимости описывается вторым слагаемым формулы (1). Ясно, что в области высоких температур проводимость будет собственной (второе слагаемое будет во много раз больше первого ) и (2) Практически при исследовании температурной зависимости электропроводности полупроводников часто пользуются не проводимостью, а сопротивлением R. Тогда по (2): (3) Если формулу (3) прологарифмировать, то: (4) Таким образом, зависимость ln R = f(1/T) является линейной и тогда угловой коэффициент этой прямой есть Тогда: В данной работе использован полупроводник, который является собственным при температуре выше комнатной. Измерив зависимость R(T) можно определить ∆E - ширину запрещенной зоны - важную характеристику полупроводника. |
