ЛАБОРАТОРНЫЕ РАБОТЫ ПО АТОМНОЙ И КВАНТОВОЙ ФИЗИКЕ. Практикум по физике (атомная и квантовая физика) Направление подготовки 010700 (510400) Физика
 Скачать 2.87 Mb. Скачать 2.87 Mb.
|
|
Задание 2. Определение мертвого времени счетчика 1. Поместить в свинцовый домик 1-й источник. Измерить счет N1 за 10 сек. 2. Поместить в свинцовый домик 2-й источник. Измерить счет N2за 10 сек. 3. Измерить n12счет, когда в домике находятся 1-й и 2-й источники, за 10 сек. Результаты измерений занести в таблицу 2. Таблица 2
5. По формуле (2) рассчитать мёртвое время счётчика τ. 6. Сформулировать выводы по работе. Контрольные вопросыНазначение газоразрядных счетчиков. Устройство счетчика Гейгера - Мюллера. Физические процессы, протекающие при прохождении через счетчик ионизирующей частицы. Схема включения счетчика Гейгера - Мюллера в электрическую цепь. Эффективность счетчика. Счетная характеристика счетчика. Разрешающее время счетчика. Экспериментальное определение мертвого времени счетчика. Рекомендуемый список литературы 1. Савельев И.В. Курс общей физики: Учеб.: В 3т.Т3.– М.: Наука, 1987.–304с. 2. Сивухин Д.В. Общий курс физики: Учеб.: В 5т.Т5.Ч2. – М.: Наука,1986. – 416с. 3. Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Курс общей физики. Оптика и атомная физика.– М.: Просвещение. 1992.–320 с. ЛАБОРАТОРНАЯ РАБОТА №9Определение коэффициента поглощения β-излучения и верхней границы β-спектра Цель работы:экспериментальное изучение кривой поглощения β-излучения в алюминии, определение коэффициента поглощения β-излучения, оценка верхней границы энергии β-спектра. Оборудование:прибор «Арион» со свинцовым домиком, источник β-излучения, набор алюминиевых пластин. Краткая теория Естественной радиоактивностью называется самопроизвольное превращение одних атомных ядер в другие, сопровождающееся испусканием определенного вида излучений. Явление радиоактивности было открыто в 1896 году французским физиком Анри Беккерелем. Естественная радиоактивность наблюдается, как правило, у тяжелых элементов, располагающихся в конце периодической системы. Радиоактивное излучение оказалось самопроизвольным и постоянным, оно не зависит от внешних условий: освещения, давления, температуры. Это означает, что радиоактивность определяется внутренними свойствами ядер данного элемента. Радиоактивное излучение, проходящее через магнитное или электрическое поля, разделяется на три потока: α-, β- и γ-лучи. Дальнейшие исследования показали, что положительно заряженные α-лучи состоят из ядер гелия; β-лучи оказались потоком электронов, летящих со скоростью, близкой к скорости света и с энергией до 10 МэВ; γ-лучи, не отклоняющиеся магнитным полем, представляют собой жесткое электромагнитное излучение с большой проникающей способностью, по свойствам напоминающее рентгеновские лучи высокой энергии. Радиоактивные излучения вызывают посерение фотопластинок, ионизируют газ или конденсированное вещество, через которое они проходят. Эти свойства лежат в основе экспериментальных методов регистрации и исследования свойств радиоактивного излучения. Превращение ядер, сопровождающееся испусканием α- и β-лучей, называется соответственно α- и β-распадом; γ-излучение ядер не является самостоятельным видом радиоактивности, оно сопровождает процессы α- и β-радиоактивных распадов. Испускание α- и β-частиц изменяет заряд ядра, поэтому оно должно приводить к изменению химической природы радиоактивного атома. При α-распаде происходит превращение изотопов с атомным номером Z и массовым числом A в изотопы с атомным номером Z -2 и массовым числом A-4 при одновременном испускании α-частиц, являющихся ядрами изотопа He. Ядерная реакция имеет вид: При создании теории β-распада возникли особые трудности. При β-распаде изотоп с атомным номером Z и массовым числом A превращается в изотоп с атомным номером Z+1 и тем же массовым числом A при одновременном испускании β-частиц, являющихся электронами ( Существует β+-распад, при котором происходит превращение изотопа с атомным номером Z в изотоп с атомным номером Z-1 при сохранении массового числа A и с испусканием позитрона ( Электроны образуются в результате превращения внутри ядра нейтрона ( В ядре нет электронов так же, как в атоме нет фотонов. Аналогично тому, как в процессе перехода атома из одного состояния в другое излучается фотон, при переходе ядерного нуклона из нейтронного в протонное состояние испускается электрон. Так как энергетические состояния ядра дискретны, следовало ожидать, что спектр энергий β-частиц также будет дискретным. В действительности оказалось, что β-электроны имеют сплошной спектр. Одинаковые ядра испускают электроны с энергией изменяющейся от нуля до некоторой верхней границыEмакс, которая равна разности энергетических уровней ядра, испускающего β-частицы. Казалось, что часть энергии электрона куда-то бесследно исчезла, а это равнозначно нарушению закона сохранения энергии при β-распаде. В 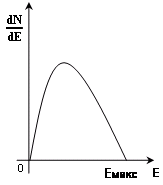 Рис. 1 Энергетический спектр электронов при β-распаде торая трудность – спин ядра (целочисленный или половинный) не изменяется в результате β-распада, хотя электрон уносит с собой половинный спин. Эти трудности устранила гипотеза Паули о том, что одновременно с β-частицей испускается еще одна, электрически нейтральная частица с ничтожно малой массой и спином равным Здесь по горизонтальной оси отложена энергия электронов Е, по вертикальной оси – Верхняя граница β-спектра у разных изотопов различна и поэтому является одной из характеристик изотопа. Значения верхней границы β-спектра у различных изотопов лежат в пределах от 15 кэВ до 15 МэВ. При прохождении через вещество пучок быстрых электронов уменьшает свою интенсивность, что позволяет говорить о поглощении β-частиц. Механизм поглощения обусловлен следующими процессами. 1.Упругое рассеяние электронов ядрами. П (1) где Если толщина d слоя мала (d<< Для больших толщин (d При многократном рассеянии (среднее число актов превосходит 20) угловое распределение рассеянных электронов является гауссовским до тех пор, пока средний угол рассеяния меньше 20°. Для (d<< 2. Рассеяние электронов на электронах. Расчет выражения для эффективного сечения рассеяния электронов на электронах приводит к выводу, что интегральное эффективное сечение 3. Ионизационные потери энергии. Взаимодействие β-частицы с электроном атома приводит к передаче ему некоторой доли энергии, следствием чего является либо вылет электрона за пределы атома (ионизация атома), либо переход электрона в более высокое энергетическое состояние (возбуждение атома). Это есть ионизационные потери энергии. Теория потерь энергии при неупругом соударении с электронами тормозящей среды, разработанная Боте, дает следующее общее выражение для удельных ионизационных потерь: Потери на излучение. Эти потери возникают при взаимодействии электронов с кулоновским полем ядер. Примером тормозного излучения является непрерывный спектр рентгеновских лучей, возникающих при торможении электронов на антикатоде рентгеновской трубки. Потеря энергии заряженной частицы на тормозное излучение называется радиационной. Относительные радиационные потери в предельных случаях выражаются соотношениями: 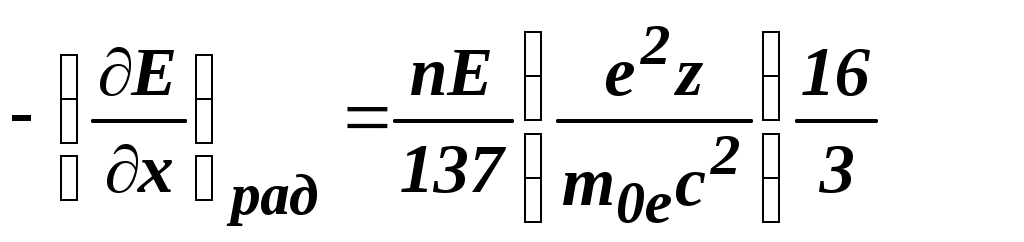 ( для β<<1); ( для β<<1);(3) 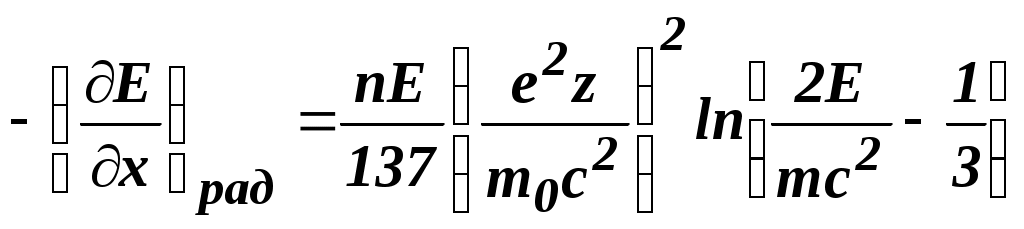 (для β≈1). (для β≈1).Таким образом, для медленных электронов радиационные потери растут пропорционально Е (релятивистская кинетическая энергия электрона), а для быстрых – несколько быстрее благодаря логарифмическому множителю. Полные потери энергии электронами складываются из ионизационных и радиационных потерь: П 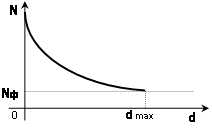 отери энергии на излучение пропорциональны приблизительно Z и увеличиваются с увеличением энергии линейно, в то же время как потери на ионизацию пропорциональны Z и увеличиваются с энергией лишь логарифмически. Поэтому при больших энергиях электронов первичного пучка преобладают энергии на излучение, а при малых энергиях будут преобладать ионизационные потери. Энергия Eкр , при которой радиационные потери становятся равными ионизационным, называется критической. отери энергии на излучение пропорциональны приблизительно Z и увеличиваются с увеличением энергии линейно, в то же время как потери на ионизацию пропорциональны Z и увеличиваются с энергией лишь логарифмически. Поэтому при больших энергиях электронов первичного пучка преобладают энергии на излучение, а при малых энергиях будут преобладать ионизационные потери. Энергия Eкр , при которой радиационные потери становятся равными ионизационным, называется критической. Н Рис. 2 Кривая поглощеия электронов в металле а пути электронов между их источником и счетчиком устанавливается поглотитель, и при этом наблюдается ослабление интенсивности электронов с увеличением толщины поглотителя. электрон с определенной энергией может проникнуть через данный поглотитель лишь определенной толщины dmax, поэтому величина ρdmax (ρ-плотность поглотителя) принимается за меру энергии электронов. Кривые поглощения электронов имеют приблизительно экспоненциальный ход (рис. 2). С 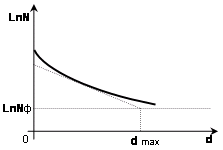 Рис. 3 Кривая поглощения электронов, построенная в полулогарифмическом масштабе толь быстрое спадание кривой поглощения при малых значениях d и сравнительно небольшое спадание в области больших d объясняется тем, что механизм взаимодействия медленных и быстрых электронов с веществом различен. Это различие приводит к тому, что быстрые частицы поглощаются сравнительно слабо и кривая поглощения ассимптотически приближается к линии фона (каждый счетчик обладает фоном, т.е. при отсутствии облучения в нем возникают разрядные импульсы, которые могут быть вызваны космическими лучами, самопроизвольными разрядами и радиоактивными примесями в материалах, из которых изготовлен счетчик). Т lnN ак как такое ассимптотическое приближение кривой к линии фона не позволяет определить точное значение dmax, то целесообразно строить кривую поглощения в полулогарифмическом масштабе lnN=f(d) (рис. 3). В этом случае можно выделить прямолинейную часть кривой поглощения и, продолжив ее до пересечения с линией фона, определить значение dmax . Так как достаточно точных формул, выражающих зависимость максимального пробега электронов от их энергии, нет, то для вычисления максимальной энергии используются эмпирические формулы, полученные разными экспериментаторами. В данной работе Eмакс определяется двумя методами. Метод полного поглощения. Для электронов с энергией 0,7 МэВ<E<3 МэВ, хорошо оправдывается соотношение Физера: где ρ - в К где N0 – число электронов до поглощения, N – число частиц после прохождения слоя d, μ – линейный коэффициент поглощения (см -1).Для определения μ необходимо выбрать на графике lnN=f(d) (см. рис. 3) примерно прямолинейный участок и из соотношения. (6’) (7) где Метод половинного поглощения. К 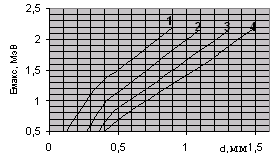 роме изложенного выше метода полного поглощения, пользуются также методом половинного поглощения, который учитывает, что при малых и больших значениях d ход кривой поглощения отличается от экспоненциального закона (см. рис. 3). Этим методом производят измерение толщины слоя половинного поглощения. Слоем половинного поглощения d называется такой слой, при прохождении которого интенсивность электронов уменьшается вдвое. роме изложенного выше метода полного поглощения, пользуются также методом половинного поглощения, который учитывает, что при малых и больших значениях d ход кривой поглощения отличается от экспоненциального закона (см. рис. 3). Этим методом производят измерение толщины слоя половинного поглощения. Слоем половинного поглощения d называется такой слой, при прохождении которого интенсивность электронов уменьшается вдвое. В Рис. 4 Кривые для определения верхней границы β-спектра се рассмотренные выше характеристики μ, μ΄, Для определения Eмакс по графику N=f(d) определяют толщины слоев алюминия, ослабляющего излучение в 21, 22, …, 2k раз. Связь между толщиной слоя алюминия d, ослабляющего в 2k раза, и максимальной энергией β-спектра экспериментально изучена и представлена в виде кривых, приведенных на рис. 4. Каждая кривая на рис. 4 соответствует своему значению k. При k=1 скорость счета уменьшается в 2 раза, при k=2 – в 4 раза и т.д. Зная толщину d, уменьшающую скорость счета в 2 раза, по графику (см. рис. 4) можно определить значениеEмакс в МэВ. Задание. 1. Подготовить лабораторную установку к работе, проверив работоспособность источника питания, секундомера и счетчика импульсов. Установить U= 450 В. 2. Измерить фон установки за t=5 мин. Он складывается из действия на счетчик: космического излучения; рассеянных частиц; тормозного излучения; β-лучей в спектре источника. Для определения Nф необходимо определить счет установки с фильтром, задерживающим все электроны (d=3 мм). 3. Снять кривую поглощения. Фольга располагается между счетчиками излучения и коллиматором. Нужная толщина фильтра достигается путем последовательного наложения алюминиевых пластинок друг на друга. Толщина пластинок измеряется микрометром. Толщину увеличивать от 0 до 3 мм, получить максимальное число точек. Начинать измерения при t=10(сек), затем увеличить время, набирая не менее 1000 импульсов в каждом измерении. 4. Заполнить таблицу 1. Таблица 1.
5. Построить графики n=f(d) и lnn=f(d), отложив на них уровень фона. 6. По графику lnn=f(d) определить dmax. 7. Пользуясь соотношением (6’) рассчитать линейный коэффициент поглощения μ. По формуле 8. Оценить верхнюю границу β-спектра Eмакс методами полного поглощения и половинного поглощения. 9. Сравнить полученные результаты с данными, известными из литературных источников. 10.Сформулировать выводы по работе. Контрольные вопросы Виды радиоактивного распада. β-распад и его закономерности. Как объяснить непрерывный энергетический спектр электронов при β-распаде? Какими основными механизмами объясняется поглощение электронов в веществе? Что такое линейный и массовый коэффициенты поглощения? В чём заключаются методы полного и половинного поглощения определения Емакс верхней границы β– спектра? Рекомендуемый список литературы 1. Савельев И.В. Курс общей физики: Учеб.: В 3т.Т3.– М.: Наука, 1987.–304 с. 2. Сивухин Д.В. Общий курс физики: Учеб.: В 5т.Т5.Ч2. – М.: Наука,1986. – 416 с. 3. Гершензон Е.М., Малов Н.Н., Мансуров А.Н. Курс общей физики. Оптика и атомная физика.– М.: Просвещение. 1992.–320 с. . ЛАБОРАТОРНАЯ РАБОТА №10Определение процентного содержания калия в смеси солей KCl и NaCl по ее β-активности Цель работы:1. определение процентного содержания калия в смеси солей KCl и NaCl. 2.определение удельной активности радиоактивного препарата относительным методом по калиевому эталону. Оборудование: прибор “Арион” со свинцовым домиком, набор образцов с различным процентным содержанием калия. |
