Практикум по физике Часть Биоакустика. Вводное занятие
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
7. Систематические и случайные погрешности. Систематические погрешности – это погрешности, вызываемые факторами, действующими постоянно (т.е. систематически). Их можно обнаружить и измерить с помощью более точных приборов. Прибор, дающий систематическую погрешность, всегда завышает или всегда занижает свои показания, то есть во всех измерениях значения абсолютной погрешности – это числа одного знака. Но по модулю она может быть от случая к случаю различной. Причины появления систематических погрешностей могут быть тривиальными (например, разрядилась батарейка), а могут быть и более коварными (непостоянство диаметра капилляра в термометре; несовершенство методики косвенных измерений). Количество возможных причин может исчисляться десятками. Единой методики выявления причин появления систематических погрешностей не существует. Вопрос для быстро соображающих: какие неожиданности грозят автомобилисту, если он контролирует расход топлива по показаниям уровнемера, а бензобак сужается книзу? Какую погрешность имеет уровнемер? Если систематическая погрешность обнаружена и оценена количественно, то возможны следующие варианты действий: - устранение ее причины; - коррекция показаний состоявшихся и будущих измерений на величину систематической погрешности; - пренебрежение систематической погрешностью, если она достаточно мала. Случайные погрешности - результат несогласованного действия группы факторов, среди которых нет доминирующих по влиянию на общий результат. Случайные погрешности имеют следующие свойства: 1. Одинаковые по модулю положительные и отрицательные погрешности равновероятны. 2. Меньшие по модулю погрешности встречаются чаще, чем большие. 3. С увеличением числа измерений одной и той же величины, среднее арифметическое значение случайных погрешностей, посчитанное с учетом их знаков, стремится к нулю. Это означает, что с ростом количества измерений среднеарифметическое значение результатов измерений стремится к истинному значению измеряемой величины. Свойство 3 - кардинальный способ уменьшения величины случайных погрешностей - увеличение количества измерений. Случайные и систематические погрешности могут спокойно сосуществовать друг с другом. 8. Нормальный закон распределения в экспериментальных исследованиях. Случайные величины, обладающие свойствами 1 – 3 предыдущего раздела, можно сказать, предрасположены к тому, чтобы иметь распределение вероятности, известное как распределение Гаусса (нормальный закон распределения). По нормальному закону распределено очень многое в самых разнообразных областях знаний. Универсальность нормального закона сумел обосновать А.М. Ляпунов. Согласно его теореме, если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин х1, х2, …, хn, влияние каждой из которых на всю сумму ничтожно мало՜, то независимо от того, каким законам подчиняются слагаемые х1, х2, …, хn, сама величина Х будет иметь распределение вероятностей, близкое к нормальному, и тем точнее, чем больше число слагаемых n. Человеческий организм – сложнейшая система; количество показателей жизнедеятельности – громадное; количество их возможных связей друг с другом – еще больше. Требование теоремы Ляпунова о том, чтобы влияние каждого из них на всю сумму было ничтожно малым, может быть выполнено в одних исследованиях и не выполненным - в других. В ходе любого медико-биологического эксперимента, накопив выборку результатов измерений некоего параметра, имеет смысл проверить ее на соответствие нормальному закону распределения, применив подобающий случаю статистический критерий (Шапиро-Уилка, Пирсона). При этом, любой результат проверки по-своему интересен. Если гипотеза о нормальном распределении принимается, вы получаете возможность применить к этому параметру все свои познания о свойствах нормально распределенных величин. Если же гипотеза не принимается, вы приходите к выводу, что среди множества факторов, влияющих на исследуемый параметр, есть доминирующие по влиянию, и их неплохо бы выявить; и это уже – призыв к действиям в нужном направлении. Что касается применимости нормального закона к погрешностям измерений, то если систематические погрешности устранены (или вычтены из результатов измерений), то по опыту исследований погрешностей в измерительных системах, оставшиеся случайные погрешности распределены по нормальному закону или очень близки к нему. Контрольные вопросы по теме «Вводное занятие». 1. Измерения. Основные единицы системы СИ. 2. Производные единицы системы СИ для частоты, силы, давления, энергии, мощности. 3. Производные единицы системы СИ для электрических и магнитных величин: заряд, потенциал, сопротивление, электроемкость, магнитная индукция, поток магнитной индукции, индуктивность. 4. Некоторые внесистемные единицы: миллиметр ртутного столба, калория, электронвольт, лошадиная сила. 5. Дробные и кратные единицы. 6. Прямые и косвенные измерения. Примеры. 7. Абсолютная и относительная погрешность измерений. Методы оценки абсолютной погрешности. 8. Доверительный интервал. Доверительная вероятность. Уровень значимости. 9. Систематические погрешности, их происхождение, свойства, способы выявления и уменьшения. 10. Случайные погрешности, их происхождение, свойства, способы выявления и уменьшения. 11. Нормальный закон распределения: причины его универсальности; применение в эксперименте. БИОАКУСТИКА. ЗВУК. В этой главе рассматриваются вопросы физики слуха: - характеристики колебаний и волновых процессов; - получение, распространение и особенности восприятия звука в привычном смысле этого слова, то есть звуковых волн слышимого диапазона частот (16 Гц – 20 кГц), - строение уха, его функционирование, вопросы контроля качества слуха. Заключительный раздел – методические указания по выполнению лабораторной работы «Определение порогов слышимости с помощью аудиометра». 1. Колебания. Их характеристики. Гармонические колебания. Колебания – это процессы, характерные той повторяемостью во времени. По физической природе колебания могут быть механическими, электромагнитными, смешанного типа. Простейший пример механической колебательной системы - грузик, качающийся на нити. Воспользуемся этой легко представимой системой, чтобы систематизировать сведения о колебаниях как таковых, об их общепринятых характеристиках и единицах их измерений. Свободные колебания - это колебания в системе, выведенной из состояния равновесия и предоставленной самой себе. Если грузик отклонить на нити и отпустить, начнутся его свободные колебания. Собственная частота (частота собственных колебаний) – это частота свободных колебаний в системе, В примере с грузиком она зависит от длины нити и от ускорения свободного падения в данной местности. Причины возникших колебаний: действие силы тяжести, инерция грузика и то, что мы, первоначально отклонив грузик, сообщили ему некоторую механическую энергию. Отпустив отклоненный грузик, мы предоставили ему возможность совершать свободные колебания. Однако свободные колебания грузика будут затухающими. Причины - потери энергии на преодоление сил сопротивления. Период колебаний Т - длительность одного полного цикла колебаний. Периодические колебания характерны постоянством периода; пример - колебания грузика на нити. А вот колебания любых характеристик сердца (механических, электрических, магнитных) не являются строго периодическими даже при нормальной работе сердца. Частота колебаний ν- количество колебаний в единицу времени. Частота обычно измеряется в герцах. Если колебания таковы, что за одну секунду происходит один их полный цикл, то их частота - 1 Гц. Для более частых колебаний применяются кратные герцу единицы: 1 кГц = 10 3 Гц; 1 МГц = 10 6 Гц; 1 ГГц = 10 9 Гц, 1 ТГц = 10 12 Гц. Частота и период взаимно обратны: ν = 1/Т; Т=1/ν. Что колеблется в примере с колебаниями грузика на нити? Прежде всего вспоминаются зрительные образы: происходит непрерывное изменение положения грузика в пространстве, с характерной для колебаний повторяемостью положений. Но это далеко не все, что колеблется в этом примере. Колебаниям подвержены горизонтальная и вертикальная координаты грузика, его скорость и ускорение, его кинетическая и потенциальная энергия, угол отклонения нити и сила ее натяжения. Этот перечень можно бы и продолжить. Гармонические колебания - это колебания, при которых характеризуемая величина y изменяется во времени t по закону синуса или косинуса: y = А sin ( ω t + φ0 ) или y = А cos ( ω t + φ0 ) (1) Здесь А – амплитуда колебаний – наибольшее отклонение величины y от ее значения в положении равновесия системы (или от другой, более удобной, стадии колебаний); ω - так называемая циклическая частота; ее связь с обычной частотой: ω = 2πυ , то есть они отличаются друг от друга в 6.28 раза. (ωt + φ0) - фаза колебаний - величина, численно характеризующая стадию, в которой находится очередной цикл в любой момент времени t. В частности, при t =0 значение фазы равно φ0, и это - начальная фаза. На рис.1 показано ровно то, что значится в подписи к нему. Слева, на векторной диаграмме, показан амплитудный вектор А (его модуль равен амплитуде колебаний), образующий с горизонтальной осью x угол φ0, равный начальной фазе колебаний. Будем, напрягая воображение, равномерно вращать амплитудный вектор против часовой стрелки с постоянной угловой скоростью ω, равной циклической частоте колебаний. Проекция конца вектора A на ось y будет непрерывно меняться. На графике справа показана проекция вращающегося вектора А на ось y как функция времени t : y = A Sin ( ω t + φ0 ) 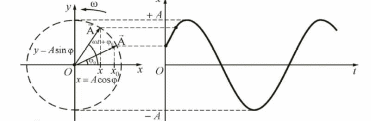 Рис. 1. Гармонические колебания как проекция равномерного вращения вектора А. Гармонические и близкие к ним колебания встречаются во многих областях знаний: механика, акустика, электромагнитные колебания. В любой из этих областей встречаются сложные колебания, которые при ближайшем рассмотрении оказываются суммой нескольких одновременно происходящих, наложившихся друг на друга простых гармонических колебаний различной частоты и амплитуды. На рис. 2 представлен пример подобного рода: сложный звук (кривая 4), возникший как сумма трех простых гармонических колебаний - гармоник. 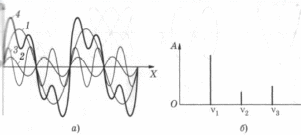 Рис.2.(a)-сложное колебание (кривая 4) как сумма трех гармоник; справа - гармонический спектр. Гармонический анализ – это разложение сложного колебания на простые слагаемые. Результатом гармонического анализа является спектр колебаний. Пример спектра приведен на рис. 2 б. Спектр колебаний - это диаграмма, показывающая, как распределяется общая энергия колебаний по различным значениям частоты. В частном случае, представленном на рис. 2 б, распределение энергии очень неравномерное: колебания происходят лишь на трех значениях частоты. К тому же, на этих частотах различна амплитуда А Спектр данного вида - линейчатый. Примечания: Чем больше амплитуда колебаний, тем больше их энергия. Более того, энергия колебаний пропорциональна квадрату амплитуды. Помимо линейчатых спектров, существуют спектры других типов: полосатые и непрерывные. В полосатых - вертикальные полосы вместо вертикальных линий. В непрерывных - отражается возможность одновременных колебаний на всех частотах широкого диапазона. Идея представления сложных колебаний в виде суммы нескольких гармоник различной частоты и амплитуды получила интересное развитие в математике, в теории приближения функций. Согласно этой теории, практически любая функция (в том числе - никак не связанная с колебаниями, и в том числе - заданная не формулой, а графиком, в том числе, графиком, полученным экспериментально или даже нарисованным прибором-самописцем); так вот, любая функция может быть приблизительно равна сумме некоторого количества гармоник. Такое представление функций, предложенное французским физиком и математиком Жаном Фурье, названо его именем: разложение Фурье. 2. Вынужденные колебания. Резонанс. Вернемся к знакомой колебательной системе: грузику на нити. В некоторых случаях лучше подойдет родственная колебательная система - обычные качели. Свободные колебания, начавшиеся в любой из этих систем после однократного толчка, будут по понятным причинам, затухающими; амплитуда будет от цикла к циклу уменьшаться. Как сделать начавшиеся колебания незатухающими? Кто хоть раз качался на качелях, согласится, что для этого надо: компенсировать потери энергии каждого цикла, то есть в каждом цикле надо подтолкнуть грузик или качели; и при этом подталкивания в течение цикла должны быть своевременными, а не когда попало. Две этих рекомендации можно сформулировать короче: частота подталкиваний должна быть равна частоте собственных колебаний. Если это требование выполнено, то возможны следующие варианты развития событий: Энергии в цикле теряется больше, чем сообщается очередным подталкиванием, т. е. компенсации не возмещают потерь. В этом случае колебания системы останутся затухающими, но продлятся дольше. Каковы потери такова и компенсация. Именно в этом случае колебания станут незатухающими, с постоянной амплитудой, и могут продолжаться неограниченно долго. Если компенсации превосходят потери, то амплитуда колебаний станет возрастать, начнут возрастать и потери энергии в цикле. Если возрастающие потери уравняются с компенсациями, установятся незатухающие колебания с некоторой возросшей амплитудой. Наконец, если источник внешних компенсирующих воздействий достаточно мощный, то колебательная система может пойти вразнос и если ее вовремя не остановить, может произойти ее разрушение. Резонанс (от фр. resonance, от лат. resono - «откликаюсь») - отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды колебаний при совпадении частоты внешнего воздействия с частотой свободных колебаний системы.  Рис. 3. Резонансное разрушение Такомского Моста (США, штат Вашингтон, 1940 год) Мост длиной 850м был разрушен порывистым ураганным ветром. 3. Звуки с линейчатым спектром. Линейчатый спектр имеют гласные звуки нашей речи, все музыкальные инструменты, звуки сольного и хорового пения. Во многих случаях звук с линейчатым спектром становится таковым не сразу, он как бы вызревает в источнике. Как это происходит, разберем на примере звука скрипки. Само название этого прекрасного инструмента - скрипка - соответствует скрипу - звуку из категории шумов, возникающему при трении смычка о струну. Этот звук имеет непрерывный спектр; энергия распределена более-менее равномерно между колебаниями широкого диапазона частот. Но благодаря явлению акустического резонанса происходит перераспределение энергии возникших было колебаний в пользу собственных частот акустической системы «струна - корпус скрипки - воздушный столб в этом корпусе». Принципиально важно: резонанс не вносит новой энергии в акустическую систему! Он перераспределяет то, что было в начальном спектре шума (скрипа), поделив эти джоули между спектральными линиями окончательного звука, с его линейчатым спектром. Колебания одной гармоники мы воспринимаем как определенный тон. Тоны - это значения частоты, на которых происходят звуковые колебания в линейчатом спектре. Основной тон - это тон наименьшей частоты в обсуждаемом линейчатом спектре. Обертоны - общее название всех тонов, кроме основного. Принципиально важно: частота обертонов отличается от частоты основного тона в целое число раз: в 2, 3, 4, … и т. д. Этому ряду соответствует иерархия обертонов: второй обертон, третий, и т.д.; см. рис. 4 и 5. 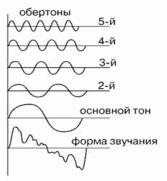 Рис. 4. Основной тон и обертоны . 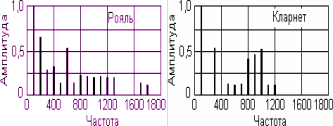 Рис. 5. У короля музыкальных инструментов - рояля оказалось 14 обертонов. Звуки человеческих голосов имеют большие различия в индивидуальных диапазонах частот. Мужские голоса обычно более низкие, а женские - более высокие. Причины тому - в том, что голосовые связки взрослых мужчин более толстые и длинные, а женские - более тонкие и короткие. Частотные диапазоны некоторых певческих голосов представлены, для общего развития, на рис. 6. Рис. 6. Диаграммы этого рисунка - мосты меж 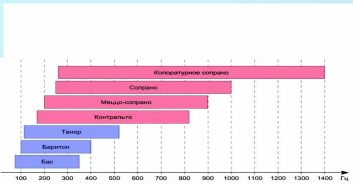 ду физикой и психофизикой. ду физикой и психофизикой.Границы каждого из семи прямоугольников устанавливают диапазон значений частоты, принятый для данного типа голоса. Частота может отсчитываться по шкале в нижней части рисунка; диапазон частот - характеристика, разумеется, физическая. Но точные измерения этих договорных частотных границ обычно не требуются, их принято определять «на слух», и это делает данные характеристики (их названия - внутри прямоугольников) характеристиками психофизическими. 4. Звуки речи с непрерывным спектром. Такие звуки возникают при «озвучивании» согласных букв. Возникают они в носоглотке: выдыхая воздух, мы с помощью языка, зубов, губ создаем на пути воздушного потока преграды с довольно резкими геометрическими формами. При обтекании этих преград течение потока становится турбулентным, вихревым. Вот вихри - то и шумят! Что такое турбулентный вихрь и почему он может шуметь? Вихрь - это временный коллектив частиц, вовлеченных в локальное вращательное движение. Вращение возникает там, где соприкасаются воздушные потоки, имеющие большую разность скоростей. Чем быстрее вращение, тем больше динамическое давление внутри вихря, и тем на столько же меньше - статическое давление в соседних с вихрем областях потока. Таково проявление закона Бернулли. Хаотичная система возникающих и исчезающих вихрей различного масштаба приводит к местным пульсациям статического давления в объеме потока, А это и есть звук. В обсуждаемых обстоятельствах возникает сложный звук с непрерывным спектром. Характер непрерывного акустического спектра, возникающего при озвучивании буквы «С», представлен на рис 7: Рис. 7. Спектр звуков буквы С. 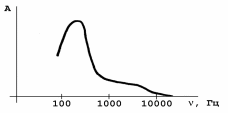 Из графика рис. 7 следует, что при произнесении звука буквы «С» возникают колебания в диапазоне частот от 100 Гц до более, чем 10 кГц. Распределение энергии по частотам весьма неравномерное: преобладают по амплитуде колебания низкой частоты (в выдыхаемом воздушном потоке преобладают сравнительно крупные вихри). Звуковые колебания с непрерывным спектром относятся к категории шумов. Белый шум – это такой шум, который вызван акустическими колебаниями примерно одинаковой амплитуды на всех частотах. Произнося звук «Ф», мы создаем что-то близкое к белому шуму. При шепоте голосовые связки расслабляются и бездействуют; частота произносимых звуков определяется в этом случае колебаниями воздуха на других препятствиях и резонансными частотами носоглотки. 5.Звуки внутренних органов. Аускультация. Перкуссия. Слабые звуковые колебания сопровождают процессы функционирования некоторых внутренних органов; сердце, легкие, органы дыхания. Звуки сопровождают пульсации в кровеносной системе. Метод диагностики, основанный на выслушивании таких звуков – аускультация (от лат. auscultatio – выслушиваю) – известен еще со времен Гиппократа. Первоначально при таком прослушивании врач прижимал ухо к телу пациента. Позднее был изобретен стетоскоп. Простейший стетоскоп представляет собой трубку с расширениями в виде воронок на ее концах. Современного терапевта трудно себе представить без стетофонендоскопа наизготовку. При аускультации применяются описательные характеристики услышанных звуков. Например, при аускультации легких оценивают громкость, продолжительность дыхательных шумов в разных фазах дыхания. Для описания качественных оттенков шумов используют такие понятия, как булькающий звук, журчащий звук, хрип, свистящее дыхание. Кстати, при измерении артериального давления по методу Короткова производится аускультация артерии в районе локтевого сгиба. Стетофонендоскоп (рис.8) – комбинированный медицинский прибор, сочетающий в себе возможности стетоскопа и фонендоскопа. Прибор имеет поворотную двухпозиционную головку. Если головка прислонена к пациенту той стороной, которая меньше по диаметру и не имеет мембраны, то прибор работает как современная версия стетоскопа. Если к телу пациента обращена мембрана (светлая на рис. 8), то прибор работает как фонендоскоп: благодаря тонкой мембране и небольшой воздушной камере между нею и корпусом головки достигается усиление звука, и что особо ценно - прослушивание звуков более высокой частоты. Название «фонендоскоп» было предложено Н.С. Коротковым, принимавшим участие в его разработке. В переводе с греческого «фон-эндо-скоп» буквально означает «звук-внутри-слушаю». В итоге, стетофонендоскоп - это двухрежимный современный стетоскоп, который обеспечивает прослушивание: - звуков низкой частоты в режиме работы без мембраны; - звуков более высокой частоты в режиме работы с мембраной. Вместо длинного названия «стетофонендоскоп» считаются вполне приемлемыми укороченные варианты «стетоскоп» или «фонендоскоп»: речь идет об одном и том же. ,  Рис. 8. Стетофонендоскоп. Перкуссия – (лат. percussion – нанесение ударов) – диагностический метод, основанный на простукивании участков тела и анализе возникших при этом звуков. По характеру звуков, возникающих при последовательном простукивании участков тела, определяют границы и расположение органов (сердце, печень, селезенка), выявляют в брюшной полости наличие свободной жидкости, оценивают состояние легких, желудка, и т.п. Метод перкуссии возник в середине восемнадцатого века. Стучат при перкуссии по-разному. Иногда – пальцами по телу (например, по грудной клетке). Иногда – пальцами по пальцам другой руки, прижатым к телу пациента. Вместо пальцев другой руки может применяться плессиметр – пластина, изготовленная из металла, дерева, пластика или кости. А стучат по плессиметру или пальцами, или специальным молоточком. Характер возникающих при ударе вынужденных колебаний зависит от выбора из перечисленного. Глубина проникновения звуков в ткани пациента – 6 – 7 см. Наибольших успехов в реализации метода перкуссии достигают те, кто имеет музыкальный слух и большой непрерывный стаж работы с применением этого метода. В современной медицине у метода перкуссии два серьезных конкурента: рентгенография и УЗИ. 6.Волны. Характеристики волн. Волна- это процесс распространения колебаний в той или иной среде. Звуковые волны - это процесс распространения механических колебаний в упругой среде. Упругая среда может быть газообразная, жидкая, твердая. Частота колебаний определяется источником звука. Диапазон слышимых частот:16 Гц — 20000 Гц. Механические колебания в упругой среде, частота которых - за пределами диапазона слышимых (человеком) частот, имеют следующие наименования: частота менее 16 Гц - инфразвук; частота от 20 кГц до 1 ГГц — ультразвук; частота более 1ГГц - гиперзвук Фронт волны - это поверхность, разделяющая в данный момент времени уже охваченную и еще не охваченную колебаниями среду. Во всех точках фронта волны колебания начинаются одновременно. Поэтому в дальнейшем колебания во всех этих точках остаются синхронными, то есть одинаковыми по фазе. Сферическая волна - это волна, имеющая фронт в виде сферы непрерывно увеличивающегося радиуса. Плоская волна - это волна с плоским фронтом. Луч – это перпендикуляр к фронту волны. Более привычны для нас световые лучи, но в акустике понятие «луч» не менее продуктивно. Акустические лучи, подобно световым, подчиняются законам геометрической оптики: прямолинейны в однородной среде, отражаются и преломляются на границе раздела двух сред. Колебания, достигшие любого слоя среды, становятся причиной возникновения колебаний в слое соседнем, и так далее. Энергия, необходимая для возбуждения колебаний во все более отдаленных областях -это энергия источника: от источника вдоль лучей распространяются потоки энергии. Интенсивность излучения I (звука, ультразвука, света, и т. п.) - это мощность потока энергии, приходящаяся на один квадратный метр поперечного сечения потока. Единица измерения этой энергетической характеристики: 1 Вт/м2. Фронт волны не стоит на одном месте. Скорость звука – это скорость перемещения фронта звуковой волны. Скорость света - это скорость перемещения фронта световой волны. При этом важно понимать, что частицы вещества в среднем остаются там же, где и были до появления звука. Скорость звука – это, по сути, скорость передачи возмущения от одних частиц к другим, но не скорость переноса вещества. Звуковые волны в газах и жидкостях - это продольные волны. В продольной звуковой волне частицы (молекулы, атомы, ионы) совершают колебания вдоль луча, т.е. колеблются вдоль направления распространения звука. В твердых телах взаимодействие частиц друг с другом имеет более сложный характер: сдвинешь одну молекулу - она подтолкнет соседнюю, оказавшуюся на пути, а заодно потянет за собой и те, что выше, и те, что ниже, и левых соседок, и правых, и в итоге могут возникнуть как продольные, так и поперечные волны. В поперечной волне колебания происходят в направлении, перпендикулярном лучу (поперек луча). Заметим, что электромагнитные волны любых видов и в любых средах- это поперечные волны. Попытайтесь вспомнить, что именно в них колеблется поперек луча и распространяется в вакууме со скоростью 300 000 км/с. Длина волны – это расстояние λ, на которое смещается фронт волны за время, равное периоду колебаний Т: λ = VТ. Здесь V- скорость звука. На концах отрезка луча протяженностью λ происходят колебания, одинаковые по фазе, поскольку на одном конце такого отрезка они возникли на время Т раньше, чем на другом. Таким образом, длина волны λ характеризует периодичность волны в пространстве, а период колебаний Т - во времени. 7. Восприятие звука. Закон Вебера – Фехнера. Диапазон интенсивности звука, в котором работает наш слух, чрезвычайно широк. На частоте звука 1кГц для среднестатистического человека характерны следующие энергетические границы: порог слышимости - 10 -12 Вт/м2; порог болевого ощущения - 10 Вт/м2. Следовательно, самый тихий и самый громкий звук отличаются по интенсивности в 10 13 раз! Во столько же раз отличаются значения массы 1 миллиграмм и 10 000 тонн! Э. Вебер сумел понять, как человек приспособился к условиям, в которых внешнее воздействие может меняться в столь широком диапазоне. Свое понимание этого приспособительного механизма он сформулировал в виде закона, согласно которому если интенсивность раздражителя возрастает по закону геометрической прогрессии, (например, так: 1, 10, 100, 1000, …), то ощущения будут усиливаться по закону арифметической прогрессии, (1, 2, 3, 4, …). Г. Фехнер выразил эту особенность ощущений на языке логарифмической функции, и в итоге закон Вебера - Фехнера состоит в следующем: Нашим ощущениям соответствуют логарифмы относительных изменений внешних воздействий. Присмотритесь: в нашем примере числа 1, 2, 3, … действительно являются десятичными логарифмами чисел ряда 10, 100, 1000. … Закону Вебера-Фехнера соответствуют наши ощущения как звуковых, так и световых ощущений. Ведь наше зрение тоже функционирует в широчайшем диапазоне: от единичных квантов на колбочку или палочку до громадных световых потоков в солнечный день. А вот в тактильных ощущениях диапазон внешних воздействий, от «чуть-чуть» до болевого ощущения, гораздо более узкий, и приспособительные логарифмические реакции на уровне ощущений не потребовались. 8. Децибельная шкала интенсивности звука Закон Вебера - Фехнера подсказывает, что при работе с величинами, способными отличаться друг от друга на много порядков, целесообразно перейти от этих чисел к их логарифмам. Единица измерения интенсивности звука в логарифмической шкале - бел (в честь Белла, изобретателя телефона). Но практически более удобной оказалась единица, в 10 раз меньшая – децибел: 1Б = 10дБ. Интенсивность звука I, измеренная в Вт/м2, и интенсивность звука Е, измеренная в децибелах связаны друг с другом следующим образом: Е = 10 lg I/I0 Здесь под знаком логарифма – дробь, которая как раз и представляет собой относительное изменение внешнего воздействия от порогового значения I0 до некоторого обсуждаемого значения интенсивности I . Приведем пример использования децибельной шкалы. Пусть при измерении уровня шума в помещении интенсиметр показал 10 мкВт/м2. Найдем, сколько это будет в децибельной шкеле. Решение: Показания интенсиметра: I = 10 мкВт/м2 = 10-5 Вт/м2. Порог слышимости: I0 = 10 -12 Вт/м2. Следовательно, интенсивность звука в децибелах: E = 10 lg I/I0 = 10 lg 10-5/10-12 = 10 lg 107 = 10 ‧7 = 70 дБ Другой пример: человек имеет повышенную остроту слуха и способен слышать звуки более тихие, чем среднестатистический порог слышимости. Если он слышит при I = 10-14 Вт/м2, то в децибельной шкале такой сверхтихий звук имеет интенсивность: E = 10 lg 10-14/10-12 = 10 lg 10-2 = 10‧(-2) = -20 дБ Порогу болевых ощущений соответствует уровень интенсивности 130 дБ. Звуки, интенсивность которых превосходит 130 дБ, как звуки нами уже не воспринимаются. Звуку с интенсивностью I0 = 10 -12 Вт/м2 (порог слышимости) в децибельной шкале соответствует Е = 0 дБ. Табл. 1. Сведения об уровнях интенсивности звука в некоторых случаях.
9. Восприятие звука: продолжение. Наибольшая острота слуха у мужчин – в среднем на частоте 4 кГц, а у женщин – в диапазоне от 4 до 6 кГц. При этом имеет значение индивидуальная протяженность слухового прохода. Существование частот, характерных повышенной остротой слуха, объясняется явлением акустического резонанса. Вот как все происходит. Звуковая волна проходит сквозь слуховой проход и отражается от барабанной перепонки. При этом отражении перепонка испытает импульс акустического давления как первый вклад колебаний этого цикла в наше ощущение звука. Но отраженная волна, выходя из слухового прохода, накладывается на колебания следующего цикла, идущие в сторону перепонки. На обсуждаемых резонансных частотах имеет место счастливое стечение обстоятельств: длина звуковой волны, длина слухового прохода и длительность прохождения этого прохода туда и обратно таковы, что накладываются колебания, одинаковые по фазе. Отраженная волна предыдущего цикла резонансно усиливает прямую волну следующего цикла, и это будет ее второй вклад в наше ощущение звука. Параметр «длина волны» имеет следующую особенность: если волна переходит из одной среды в другую, то значение длины волны меняется. Так, если скорость звука в воздухе составляет 330 м/с, а в воде – 1480 м/с, то при переходе из воздуха в воду значение длины волны возрастает почти в пять раз. Однако наше восприятие звука при этом не изменится: тенор басом не запоет. Ощущение высоты тона определяется частотой звука, а она при этом не меняется. Аналогично обстоят дела и со световыми волнами при их переходе из одной среды в другую. При переходе из воздуха в воду красный свет зеленым не становится. Бинауральный эффект. Так называется наша способность определять направление на источник звука. Лучше всего это удается, когда звуки или шумы имеют резкое начало или обладают повторяющимися характерными особенностями. Решающим фактором является разность во времени появления звукового ощущения в левом и правом ухе. Мы уверенно различаем запаздывания по времени до 10-4 с; для звука на частоте 1000 Гц это составляет 0,1 периода колебаний. Этим данным и тому факту, что расстояние между ушами – около 20 см, соответствует точность определения направлений Δφ = ± 10˚ (на частоте 1000 Гц). «Разностные тоны». При большой интенсивности звука мы можем слышать даже звуки, которых нет. Наряду с ощущениями, соответствующими реально действующим частотам ν1 и ν2 мы начинаем слышать разностные тоны (ν1 - ν2) и комбинированные тоны (ν1 + ν2) или (2ν1 - ν2). Благодаря этим причудам восприятия, мы из плохонького динамика в наушниках слышим низкие частоты, на воспроизведение которых он не способен. Стереофоническое звучание технически обеспечивается от двух акустических колонок, каждая из которых воспроизводит звук, специально для нее записанный. Звуки от двух колонок накладываются друг на друга, создавая в нашем восприятии иллюзию «живого» звучания группы музыкальных инструментов, группы участников разговора, рассредоточенных в пространстве. Менее известно, что получая монофонический звук от одной колонки, мы и его воспринимаем как стереофонический; кто-то в большей степени, кто-то – в меньшей. Колебания одной гармоники мы воспринимаем как определенный тон. Каждый тон имеет некоторую высоту. Высота тона – это качество ощущения, и как таковое физическому измерению не доступно и относится к категории психофизических характеристик звука. Наше ощущение высоты тона зависит от частоты звуковых волн, но в некоторой степени и от их интенсивности. На несинусоидальные колебания мы реагируем ощущением сложного звука, обладающего тембром. Наше ощущение тембра соответствует линейчатому спектру источника звука и распределению энергии по линиям спектра. При этом изменение частоты основного тона не меняет наших ощущений тембра. Мы различаем голоса людей и музыкальные инструменты по их тембру. Свойства акустического спектра как категории физической, определяют наши ощущения тембра как категории психофизической, физическим измерениям не доступной. Если звук, произнесенный в помещении, затухает быстро, он воспринимается как приглушенный, как бы не до конца расслышанный. Если же произнесенный звук, многократно отражаясь, долго не затухает, то помещения с таким звучанием мы называем гулкими. Приглушенность, гулкость – оценки психофизические. Им соответствует измеряемая физическая величина – время реверберации, под которым понимается время, за которое затухающий звук уменьшает свою интенсивность в 106 раз. В хороших концертных залах время реверберации на средних частотах составляет 1-2 секунды. Для достижения оптимального времени реверберации стены и перекрытия отделываются элементами, сочетающими свойства декоративные со свойствами поглотителей или отражателей звука. В состав современных электронных музыкальных комплексов входят ревербераторы – устройства, с помощью которых «длительность послезвучания» может меняться по усмотрению исполнителей. На рис. 9 представлены амплитудно-частотные диапазоны звуков речи и музыки. . Нижняя кривая соответствует порогу слышимости, а верхняя - порогу болевых ощущений. Из графиков следует, что диапазон частот речевого общения приходится на частоты от 100Гц до 8 кГц 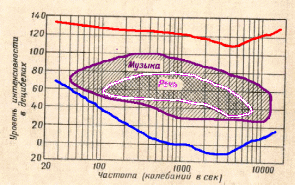 Рис. 9. Амплитудно-частотные диапазоны речи и музыки. 10. Звуки в животном мире. Все познается в сравнении. Диапазон слышимых частот человека: 16 Гц - 20 кГц. А как у братьев наших меньших? По – разному: Кошки 45 Гц - 60 кГц Собаки 15 Гц - 40 кГц Дельфины 40 Гц -200 кГц Летучие мыши 2 кГц - 180 кГц Слоны от 1 Гц Медузы 8 Гц - 15 Гц Бабочки 10 кГц - 260 кГц. 11. Физические и психофизические характеристики звука. Физические характеристики - это измеряемые величины. Определяются с применением измерительных приборов. Психофизические характеристики не измеряемы количественно. Они представляют собой сложившуюся систему субъективных качественных оценок физических процессов и явлений. Многие физические оценки имеют психофизического «родственника». В нижеследующей таблице 2 приведены подобные родственные пары, сложившиеся в акустике: Таблица 2.
Известно утверждение, что всякая классификация обедняет объект классификации. В порядке подтверждения этого спорного утверждения заметим, что громкость звука – психофизическая оценка, часто измеряемая количественно в децибелах. 12. Строение уха. Слух по воздушной и костной проводимости. Наш слух работает по двум каналам звукопроведения: по воздушному и по костному. Канал воздушной проводимости: внешний источник звука - воздушная среда - наружное ухо - среднее ухо - внутреннее ухо. Канал костной проводимости: наш голосовой аппарат - кости черепа - внутреннее ухо. Наш орган слуха – ухо – «обслуживает» оба канала звукопроведения; его схема представлена на рис. 10. Когда мы говорим сами, работает в основном канал костной проводимости: звуки возникают в носоглотке, и от ее стенок передаются костям черепа., вклад звуковых колебаний, приходящих кружным путем через воздушную среду, почти нулевой. Когда слушаем, что говорят другие, работает канал воздушной проводимости. Если мы, нырнув, что-то слышим под водой, то мы слышим по каналу костной проводимости; канал воздушной проводимости заблокирован. 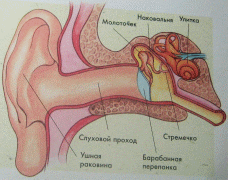 Рис. 10. Строение уха. . Мы слышим сами себя не совсем так, как нас слышат другие. В этом легко убедиться, записав разговор на магнитофон. При прослушивании записи голоса ваших собеседников будут звучать как обычно, и только ваш голос будет звучать «не так»: обнаружится, что ваш голос звучит немножко выше, чем вы привыкли считать. Это объясняется тем, что высокочастотные компоненты произносимых нами звуков возникают в основном на выходных участках голосового аппарата и передаются в механизм костной проводимости слабее, чем низкие частоты. Потеря слуха по каналу воздушной проводимости не означает переход в категорию глухих: если кортиев орган внутреннего уха – в порядке, то выручит слуховой аппарат и костная проводимость. Рассмотрим цепочку преобразований звуковых колебаний по воздушному каналу. Он начинает свою работу с поступления звуковых волн в наружное ухо. Наружное ухо: ушная раковина, слуховой проход, барабанная перепонка. Ушные раковины играют определенную роль, когда мы определяем, откуда исходит звук. Но многие животные используют ушные раковины гораздо эффективнее, чем мы. По слуховому проходу звук передается на барабанную перепонку, вызывая ее вынужденные колебания. Как мы убедились, глубина этого прохода оказывает влияние на остроту нашего слуха (см. явление акустического резонанса). Среднее ухо тоже заполнено воздухом; полость среднего уха сообщается с наружной атмосферой через евстахиеву трубу, выходящую в носоглотку. Однако передача звуковых колебаний в среднем ухе осуществляется не по воздуху, а через миниатюрную механическую систему косточек-рычагов. Внутреннее ухо заполнено жидкостью (перилимфа). Без жидкостного наполнения внутреннего уха его нежный и чувствительный кортиев орган не смог бы выполнять свои функции. Но прямая передача звуковых колебаний из воздушной среды в жидкую была бы крайне неэффективной: на границе «воздух-жидкость» звук отразился бы на 99,9%, и лишь чуть больше 0,1% энергии колебаний передалось бы в жидкость. Эволюция распорядилась следующим образом: передачу звуковых колебаний от барабанной перепонки во внутреннее ухо выполняет система миниатюрных косточек среднего уха, с причудливыми названиями: молоточек, наковальня, стремечко. Более того, эта система выполняет функции усилителя колебаний. Она обеспечивает 26-кратное повышение давления в жидкости среднего уха, в сравнении с тем акустическим давлением, которое действует на барабанную перепонку. Косточки среднего уха имеют совокупность связок, сухожилий и мышц. Сокращение этих мышц происходит рефлекторно в тех случаях, когда поступает звук чрезмерной интенсивности. Усилительный механизм косточек отказывается усиливать колебания, которые и без того слишком сильны. Такова защита внутреннего уха от акустических перегрузок. Кортиев орган преобразует звуковые колебания, переданные в перилимфу, в электрические импульсы, и отправляет их в центральную нервную систему. Эту функцию выполняют волосковые клетки. Рецепторы акустических колебаний - волосковые клетки кортиева органа. Эти клетки помещаются на базилярной мембране, а их волоски соприкасаются с покровной мембраной. Пространство между этими мембранами заполнено перилимфой. Данная слоистая структура обеспечивает всю полноту наших ощущений в мире звуков. Каждому значению частоты акустических колебаний соответствует своя зона, свой участок этой структуры, в пределах которого имеет место резонансное усиление деформаций мембран и, как следствие, возбуждение волосковых клеток, расположенных на этом участке. Таким образом, волосковые клетки различного расположения имеют различную специализацию по частоте колебаний, на которую они реагируют. Кортиев орган, благодаря особенностям строения, осуществляет спектральный анализ звуков. В диапазоне частот наибольшей остроты слуха мы способны различать значения частоты, отличающиеся на 0,3%. А по интенсивности звука наша чувствительность (то есть способность различать ее близкие значения) — просто никудышная: «сделать чуть громче» - это увеличить интенсивность в 10 раз! Зато как широк диапазон значений интенсивности звука, в котором может работать наша слуховая система! 13. Аудиометры. У каждого из нас острота слуха на разных частотах индивидуальна. Как правило, не одинаковы характеристики левого и правого уха. Аудиометр (от лат. Audio – слышу и греч. metron – мера) - это прибор, предназначенный для измерения индивидуальной слуховой чувствительности к звуковым волнам различной частоты. Главный блок аудиометра – генератор электрических колебаний звуковых частот. Генератор способен создавать колебания на ряде фиксированных значений частоты звука. Рабочий диапазон частот аудиометров – обычно от 125 Гц до 8 кГц. Этот диапазон совпадает с длиапазоном частот речевого общения (см. рис. 9). Интенсивность колебаний на любой частоте можно менять, контролируя уровень интенсивности по децибельной шкале. Электрические колебания, созданные генератором, могут создавать звуковые колебания в двух вариантах: - при исследованиях остроты слуха по каналу воздушной проводимости ток от генератора подается на динамики наушников, с переключениями «левое ухо – правое ухо»; - при исследованиях по костной проводимости ток от генератора подается на вибратор, прислоняемый к голове и создающий звуковые колебания в костях черепа без посредничества воздушной среды. В аудиометрах иногда предусматривается возможность исследовать остроту слуха на фоне непрерывных или прерывистых шумовых помех различной интенсивности. Существуют аудиометры для исследования слуха на частотах до 20 кГц. Результатом обследования на аудиометре является аудиограмма: график зависимости индивидуальных порогов слышимости от частоты звука, по каждому уху, по воздушной или костной проводимости. 14. Контрольные вопросы к разделу «Биоакустика. Звук» Колебания. Их характеристики: период, частота, амплитуда, фаза колебаний. Гармонические колебания. Спектр колебаний. Линейчатый и непрерывный акустические спектры. Примеры. Свободные и вынужденные колебания. Резонанс. Примеры акустического резонанса. Звуки с линейчатым спектром. Тоны. Основной тон. Обертоны. Тембр. Непрерывный акустический спектр. Звуки речи с непрерывным спектром. Шумы. Белый шум. Аускультация. Перкуссия. Стетофонендоскоп. Волны. Их характеристики: фронт волны, луч, длина волны. Продольные и поперечные волны. Примеры. Интенсивность. Диапазон слышимых звуков. Восприятие звука: закон Вебера-Фехнера. Децибельная шкала интенсивности звука. Восприятие звука: акустический резонанс и частота наилучшей остроты слуха; бинауральный эффект; стереофонический эффект; реверберация звука. Физические и психофизические характеристики звука. Их взаимное соответствие. Строение уха. Слух по воздушной и костной проводимости. Волосковые клетки. | |||||||||||||||||||||||||||||||||||||||
