Практикум по физике Часть Биоакустика. Вводное занятие
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
В.П. Сидоров Практикум по физике Часть 1. Биоакустика. Вводное занятие 1. Измерения. Единицы измерений в системе СИ. Измерение – это процесс сравнения исследуемой величины с ее значением, принятым за единицу. Международная система единиц СИ (System International) имеет в своей основе следующие девять единиц измерения: Таблица 1. Основные единицы системы СИ.
Из этих основных единиц выводятся все производные единицы; некоторые из них приведены в табл. 2. Таблица 2. Некоторые производные единицы системы СИ.
Заглавная буква в обозначении единицы измерения означает, что эта единица названа в честь известного физика (Герц, Паскаль, Ом, и др.). Обозначения, не связанные с именами собственными, пишутся с прописной буквы (1кг, 1кд, 1лм, и т.д.). 2. Некоторые внесистемные единицы измерений. Давление. Единица давления в системе СИ – паскаль (Па). Внесистемная единица – миллиметр ртутного столба (мм рт. ст.) Связь между ними: 1мм рт. ст. = 133 Па; 1Па = 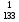 мм рт. ст. мм рт. ст.Температура – мера внутренней энергии тел. Единица температуры в системе СИ – один градус Кельвина (1К). Нулевая точка в шкале Кельвина сдвинута относительно нулевой точки в шкале Цельсия на 273,16 градуса: Т(К) = 273,16 + t(0C). Градус Кельвина (1К) и градус Цельсия (10C) равноценны. Энергия. Единица энергии в системе СИ – джоуль (Дж). Внесистемная единица – калория (кал). Связь между ними: 1кал = 4,19 Дж; 1Дж = 1 / 4,19 кал = 0,24 кал. Внесистемная единица – электронвольт (эВ) – энергия, которую приобретает электрон, прошедший ускоряющую разность потенциалов величиной в один вольт. Заряд электрона 1,6·10-19 Кл. Связь с джоулем: 1эВ=1,6·10-19 Дж. Внесистемная единица – киловатт-час (кВт‧час). Введена на основе формулы, определяющей мощность: Р = Е / t. Отсюда – выражение для энергии: Е = Р ‧ t и единица измерения кВт‧час. Эта единица широко применяется при учете производства и потребления электроэнерги. Время. Единица времени в системе СИ – секунда (с). Внесистемные единицы: 1мин = 60 с; 1 час = 3600с. Мощность. Единица мощности в системе СИ - ватт (Вт). Внесистемная единица – лошадиная сила (л.с.) Связь между ними: 1л.с. = 720 Вт = 0,72 кВт, 1кВт = 1,38 л.с. 3. Дробные доли и кратные единицы измерения. Таблица 3. Дробные доли единиц (на примере одной секунды)
Таблица 4. Кратные единицы (на примере одного метра)
Несколько сложнее обстоит дело с кратными единицами в информатике. Система повышающих приставок в таблицах 4 и 5 одна и та же: кило-, Мега-, Гига-, и т.д. Но табл. 4 соответствует десятичной системе исчисления; в ней соседние строки отличаются в 103 = 1000 раз. А в табл. 5 те же по названию приставки работают со сбоем, в котором «виновата» двоичная система исчисления: соседние строки таблицы 5 отличаются в 210 = 1024 раза. Таблица 5. Кратные единицы в информатике.
4. Прямые и косвенные измерения. Прямые измерения. Результат прямых измерений получают при непосредственном использовании измерительного прибора по его прямому назначению. Примеры прямых измерений: - Измерение размеров предмета с помощью рулетки. Если рулетка – простейшая металлическая, результат измерений считывается на ее шкале. Если это лазерная рулетка высокой точности, результат считывается с ее дисплея. - Измерение силы тока с помощью амперметра (миллиамперметра, микроамперметра), будь то прибор аналоговый или цифровой. - Измерение времени с помощью часов, с любой индикацией времени. - Измерение температуры тела пациента при помощи медицинского термометра (ртутного или электронного). Косвенные измерения. Результат косвенных измерений вычисляют с помощью какой-нибудь известной формулы, в которой одна из величин – косвенно измеряемая величина – должна быть единственной неизвестной величиной. Остальные величины, функционально связанные с измеряемой - результаты их прямых (или косвенных) измерений. Но бывает и проще: «известная формула» может соответствовать всего лишь определению измеряемой величины. Примеры косвенных измерений: - Измерение средней скорости движения. Формула соответствует определению скорости: V = S / t , где S – путь, t – длительность его прохождения. - Измерение периода полураспада радиоактивного препарата по двум результатам измерения интенсивности излучения (с помощью дозиметра) и промежутка времени между ними (с помощью обычных часов), Расчетная формула - математические следствия закона радиоактивного распада. - Измерение сопротивления проводника, Его можно получить как результат прямых измерений, если иметь омметр – прибор для измерения омического сопротивления. Если омметра нет, сопротивление проводника можно измерить косвенно, по результатам прямых измерений напряжения U на концах проводника (вольтметром) и силы тока I при таком напряжении (амперметр). Расчетная формула для сопротивления R– алгебраическое следствие закона Ома для участка цепи: R = U / I. 5. Точность. Абсолютная и относительная погрешность измерений. Точность измерений – качественная оценка близости результата измерений к истинному значению измеряемой величины. Эта интуитивно понятная категория не имеет своих собственных количественных показателей и поэтому пользуется чужими: абсолютной и относительной погрешностью измерений. Истинное значение измеряемых величин определить невозможно. Причин тому – великое множество; в каждом конкретном случае находится группа факторов, ограничивающих точность. Так что погрешности измерений неизбежны, и обязательным этапом любого измерения должна быть их количественная оценка. Факторы, приводящие к появлению погрешностей, укрупненно, могут быть связаны с особенностями исследуемого объекта, со свойствами измерительного прибора, с качествами экспериментатора. Процедуры любых медицинских измерений жестко регламентированы до мелочей (измерение артериального давления, снятие ЭКГ, и т.п.). Эти регламенты нужны, чтобы исключать возможное появление каких-нибудь дополнительных причин погрешностей. Абсолютная погрешность Δх – это отклонение результата измерения х от истинного значения измеряемой величины: Δх = х – хист. Абсолютная погрешность Δх имеет ту же размерность, что и величина х. Если вдуматься, предложенное определение абсолютной погрешности – предел совершенства; лучше – не придумаешь. Но если вдуматься еще глубже, толку от этого определения маловато, меньше, чем хотелось бы, поскольку истинное значение хист нам не известно и не будет известно никогда. Величину абсолютной погрешности приходится определять опосредованно, обходными путями. Кое-что вам знакомо из курса математической статистики. Но и она не всесильна. Некоторые методы оценки абсолютной погрешности измерений. 1. Принцип цены наименьшего деления. Школьная линейка имеет шкалу, разбитую на сантиметры и миллиметры. Цена наименьшего деления линейки – 1мм. Следовательно, измерения размеров тел с помощью такой линейки могут производиться с абсолютной погрешностью Δх ==1мм. Форма записи результата измерений (пример): L = 195±1 мм. Производители измерительной техники изготавливают шкалы приборов так, чтобы цена деления соответствовала абсолютной погрешности. 2. Абсолютную погрешность прибора можно определить с помощью другого прибора, имеющего более высокую точность измерений. 3. При проведении многократных повторных измерений, чем больше число измерений, тем меньше абсолютная погрешность средневыборочного результата. 4. Абсолютную погрешность измерений, выполняемых прибором, легко определить, если есть информация о классе прибора. Эта информация может быть указана в техническом паспорте прибора; иногда класс прибора К указан на шкале прибора, где-нибудь с краю. Согласно ГОСТ 8.401-80, класс К обозначается одним из чисел следующего числового ряда: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01. Абсолютная погрешность для результата измерения х : Δх = ± К‧хmax / 100 Пример вычислений по этой формуле: миллиамперметр класса К=0.5, предназначенный для измерения токов до Imax = 250 мА, показал силу тока I = 180 мА. Абсолютная погрешность при этом: ΔI = 0,5‧250 / 100 = 1,25 мА. Результат измерений: I = 180±1,25 мА. Правильнее записать этот результат с округлением до единиц младшего разряда результата 180, то есть считать окончательным результатом запись I = 180±1 мА. Относительная погрешность δх результата измерений – это отношение абсолютной погрешности Δх к величине xрезультата измерения: δх = Δх / х (2) Относительная погрешность – величина безразмерная. Поскольку, как правило, Δх ‹‹ х, относительную погрешность обычно выражают в процентах. Например, результату измерений I = 180±1 мА соответствует относительная погрешность δI = 1 / 180 = 0,00555 = 0,56% Относительную погрешность удобно использовать для сопоставления точности измерений, выполняемых разными методами; измерений, выполняемых в разных диапазонах измеряемой величины и даже для сравнения точности измерения разных физических величин. 6. Результаты измерений в категориях математической статистики. С точки зрения теории вероятностей величина, которая при измерениях не может быть установлена точно, может рассматриваться как случайная величина, и может анализироваться методами теории вероятностей и математической статистики, знакомыми вам по математическому блоку курса «Физика, математика». Вместе с тем, измерения – это вид деятельности, имеющий многовековую историю, сложившийся круг понятий и методов. Вам остается убедиться, что недавно изучавшаяся вами математическая статистика и традиционная теория измерений хорошо дополняют друг друга. Если бы идеально точные измерения были возможны, то каждый результат такого измерения можно бы представить, как точку, положение которой на числовой оси твердо установлено и сомнениям не подлежит. В реальных измерениях результат измерений – это некоторый интервал х±Δх (от х-Δх до х+Δх), в котором содержится истинное значение измеряемой величины – доверительный интервал. Но доверительный интервал задается в привязке к результату х состоявшегося измерения. Если провести повторное измерение, доверительный интервал может измениться. Утверждение о том, что истинное значение измеряемой величины содержится в обсуждаемом интервале, справедливо лишь с некоторой вероятностью Р, которая называется доверительной вероятностью. Величина α = 1 – Р – уровень значимости – вероятность того, что истинное значение измеряемой величины не содержится в доверительном интервале. Проведение повторных измерений приводит к уменьшению ширины доверительного интервала или к уменьшению уровня значимости и увеличению доверительной вероятности; выбор при этом – за экспериментатором. Указания, как определять границы доверительных интервалов, приведены в данном пособии в описаниях лабораторных работ всюду, где это необходимо. |
