|
|
Задания. Практикум по курсу Информатика. Часть 2
Задача 4
Используя метод прямоугольников (левых, правых и центральных), трапеций и Симпсона вычислить значение определенного интеграла:
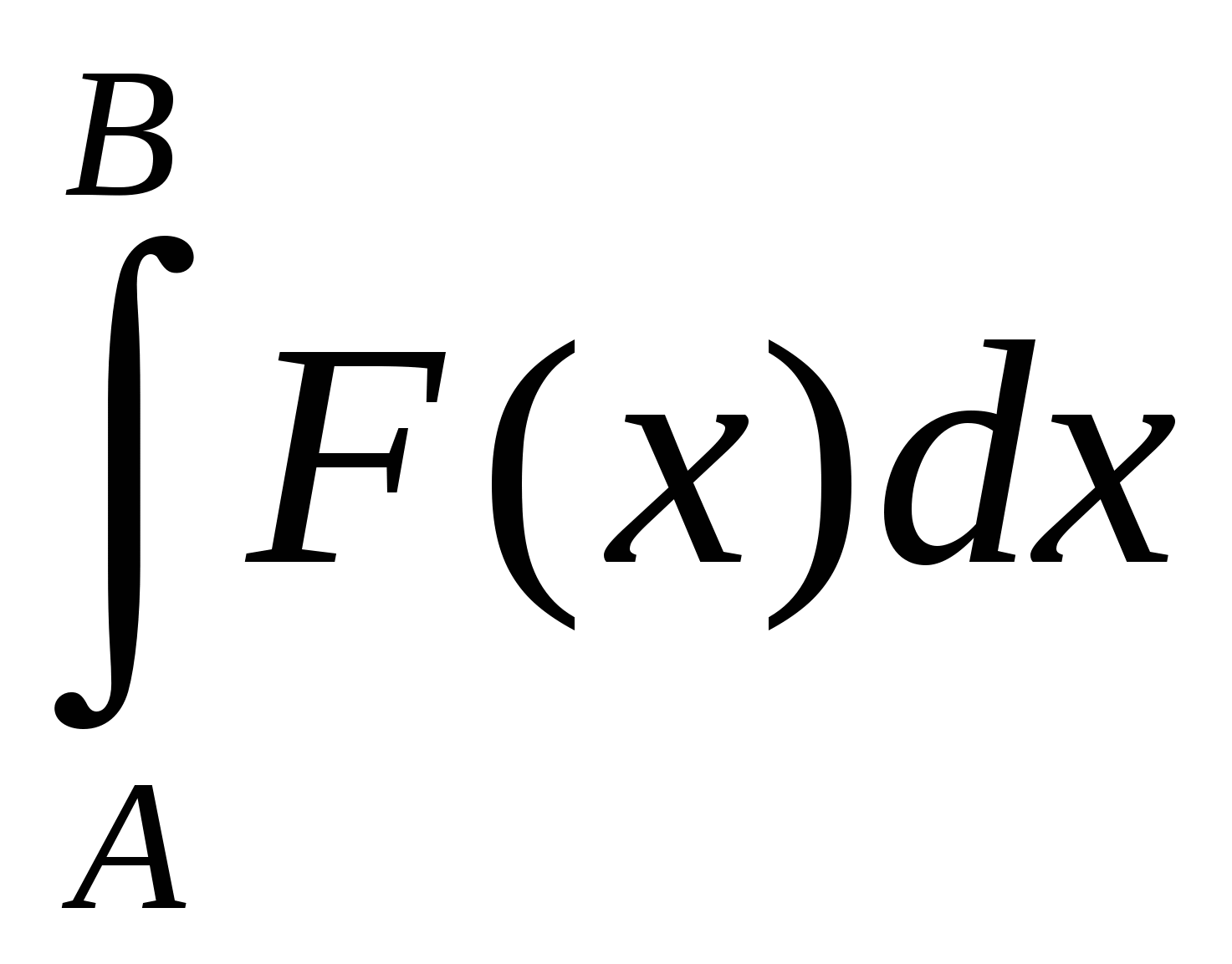 . .
Ввод пределов интегрирования и шага интегрирования (или количества разбиений) организовать с терминала. При необходимости организовать проверку возможности вычисления определенного интервала на заданном интервале. Сравнить результаты вычисления. Организовать вывод подынтегральной функции, всех исходных данных и результата вычислений на экран и в файл. При одном запуске программы предусмотреть возможность ввода разных значений для пределов и шага интегрирования (количества разбиений).
Варианты подынтегральных функций приведены в таблице Error: Reference source not found.
Таблица 6
Варианты подынтегральных функций
№
варианта
|
F(x)
|
№
варианта
|
F(x)
|
1
|
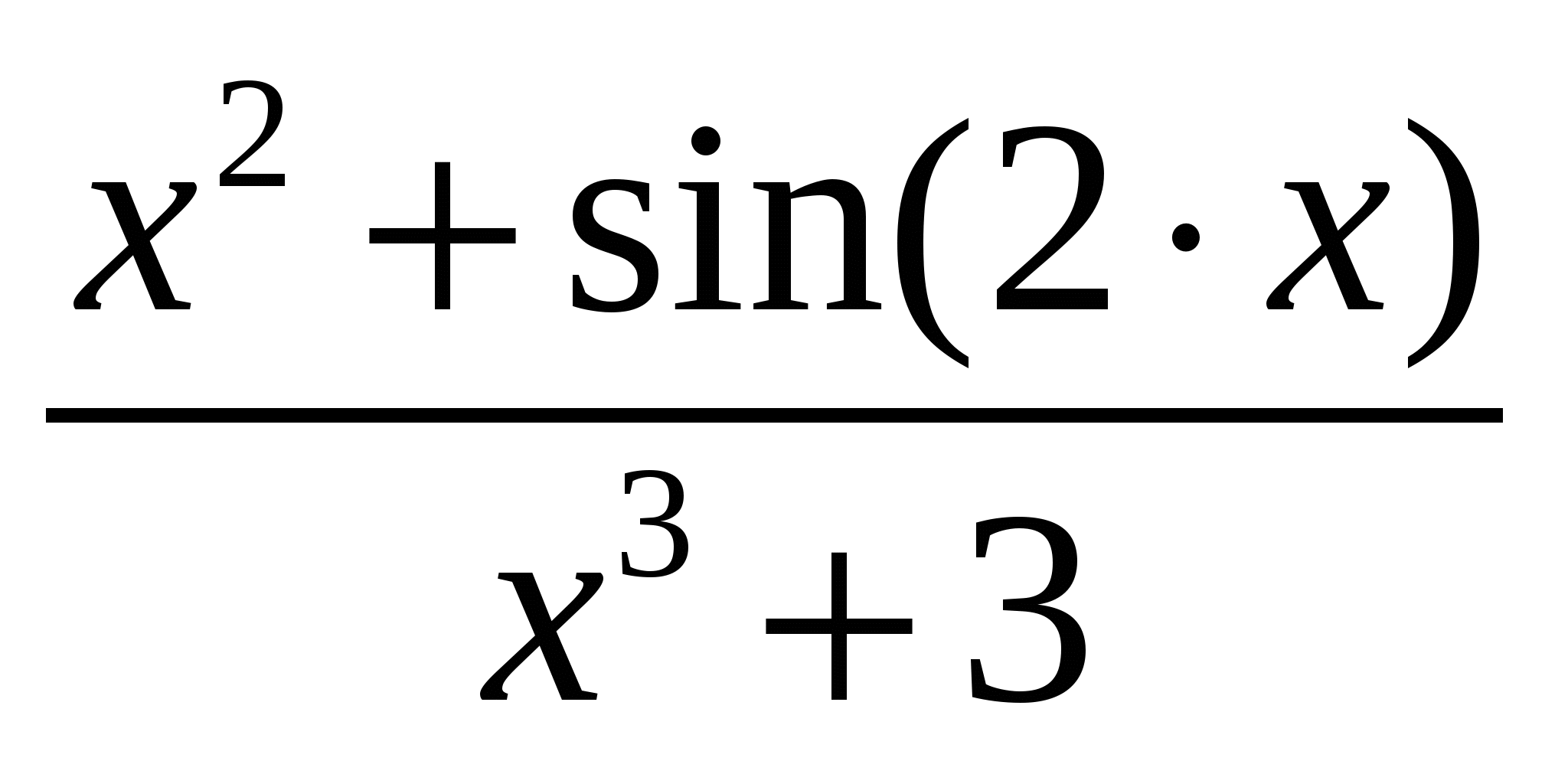
|
14
|
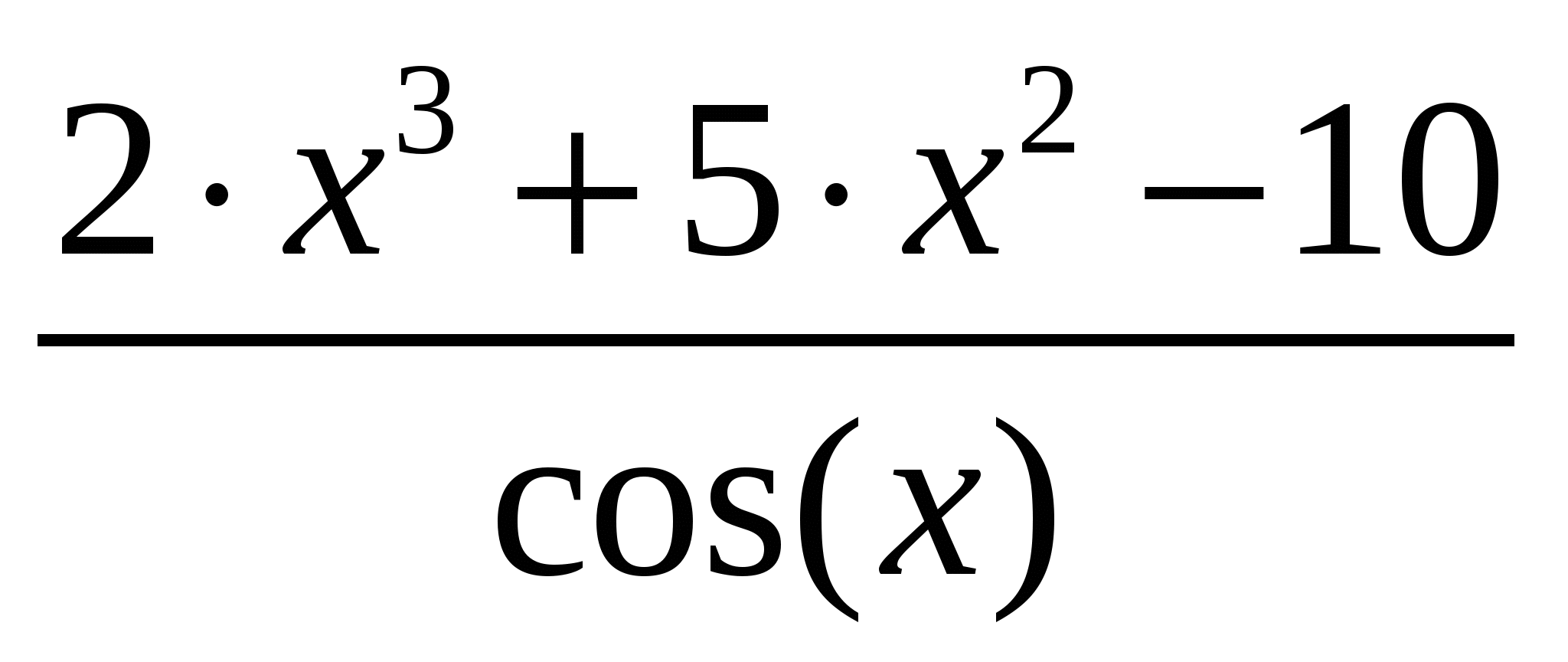
|
2
|
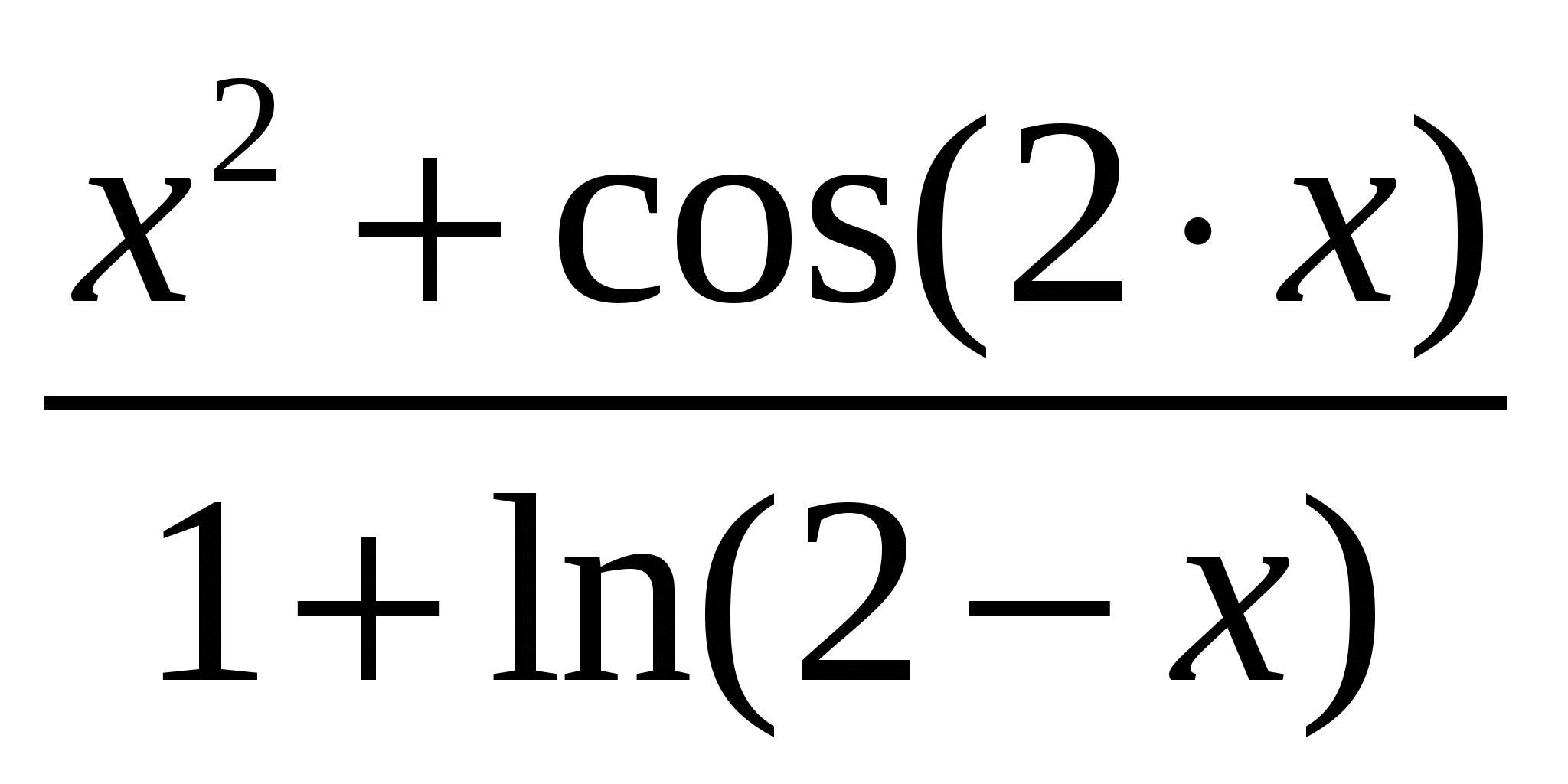
|
15
|
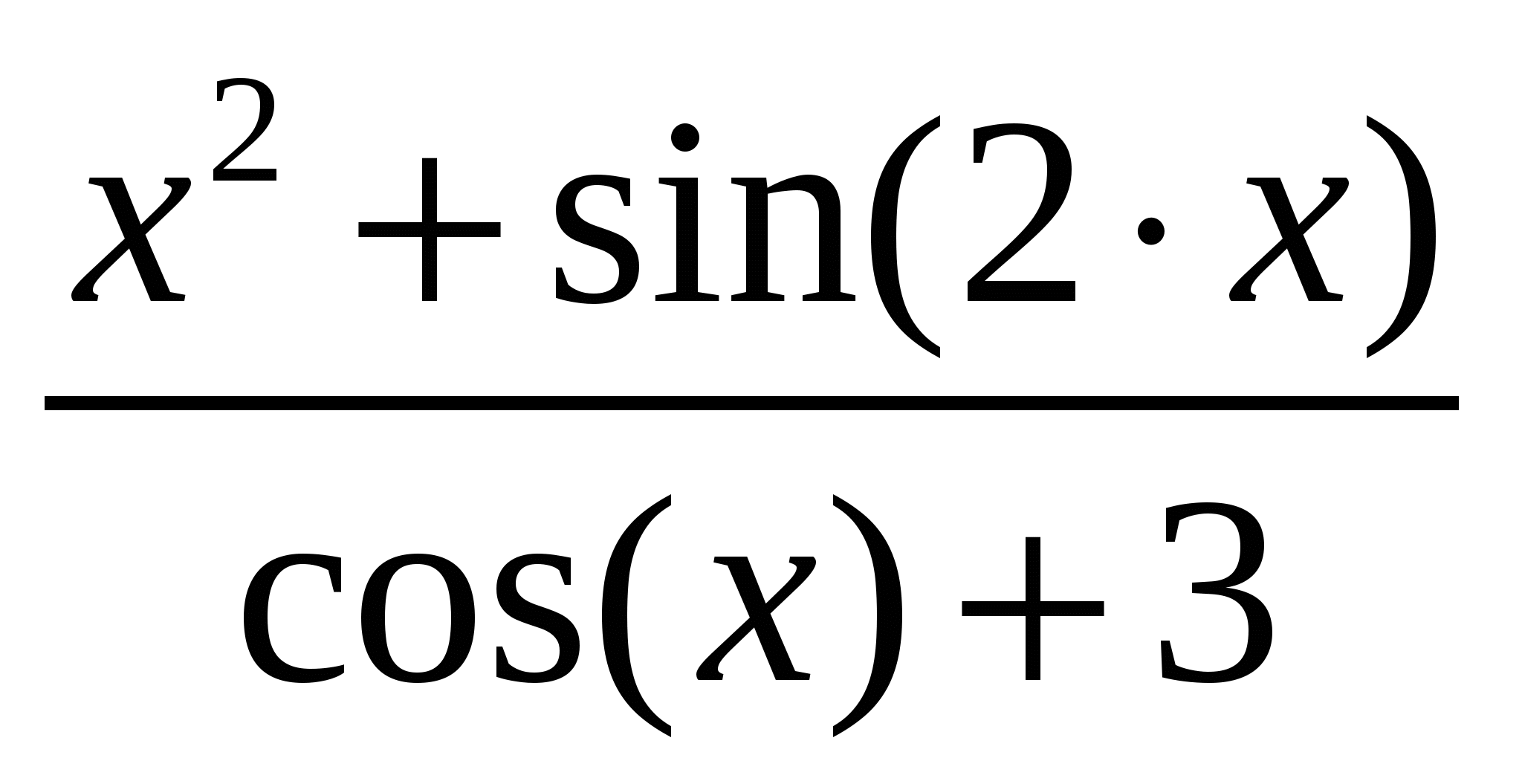
|
3
|
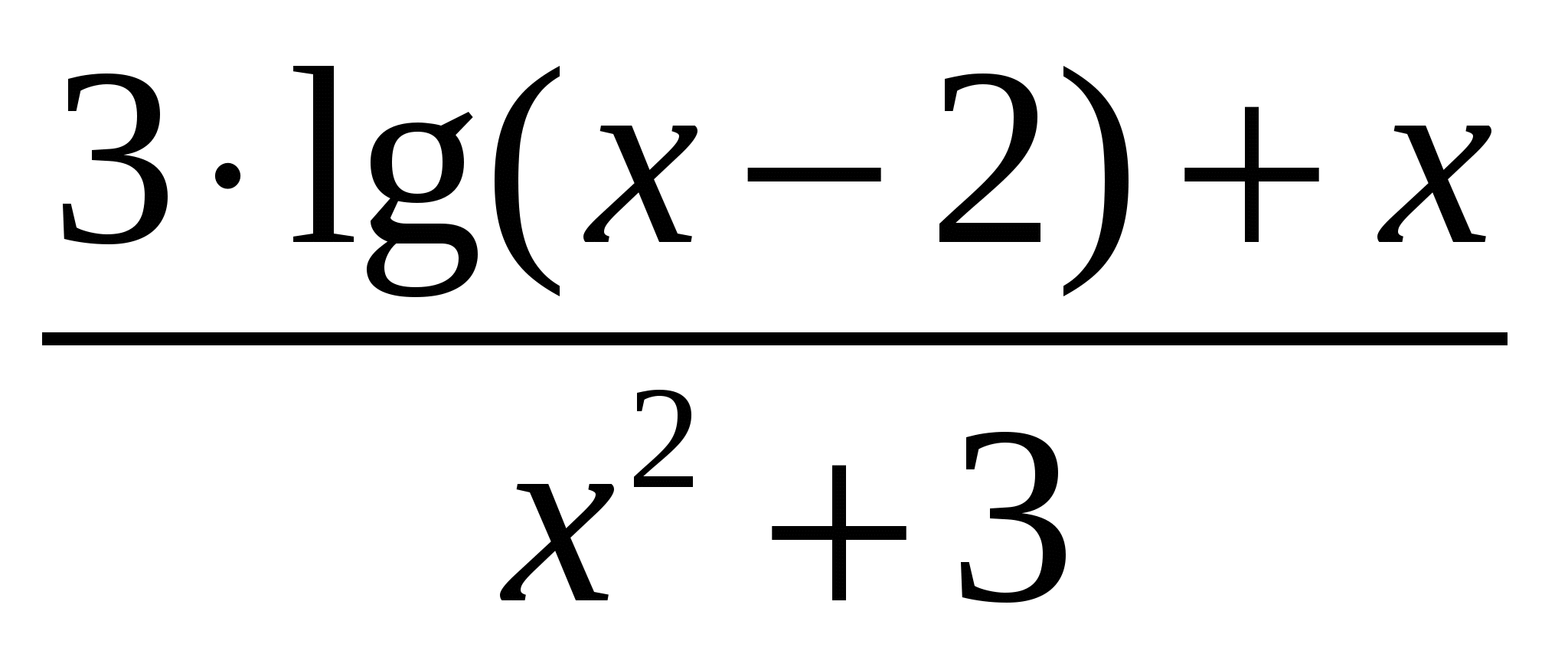
|
16
|
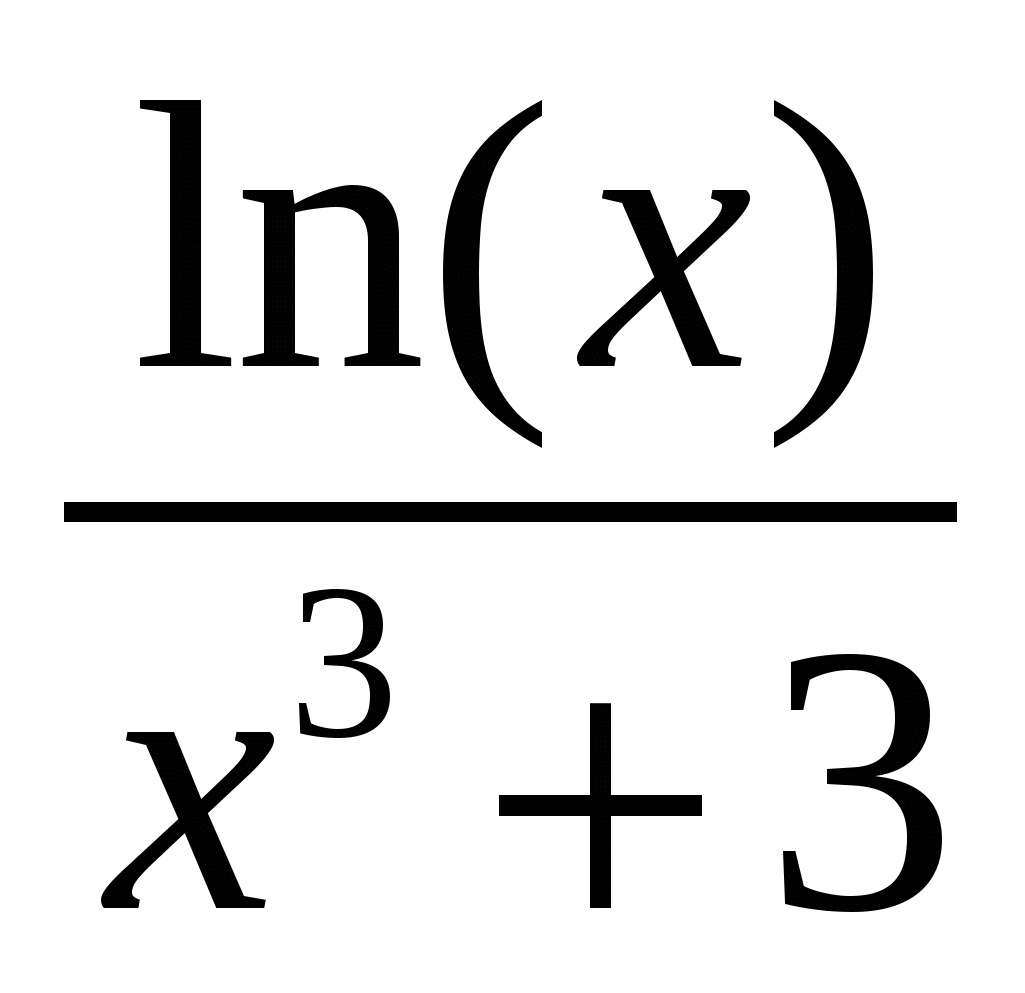
|
4
|
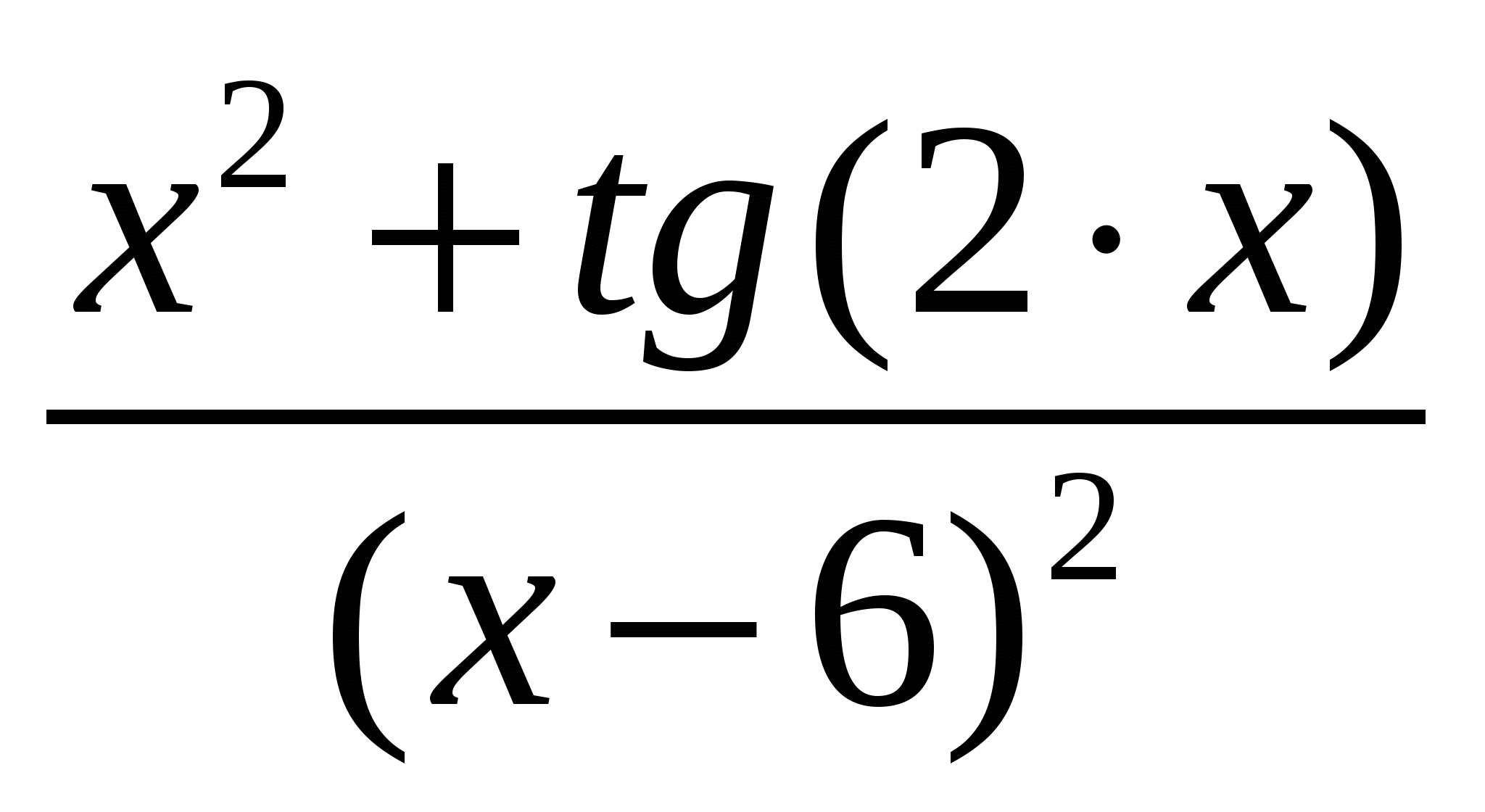
|
17
|
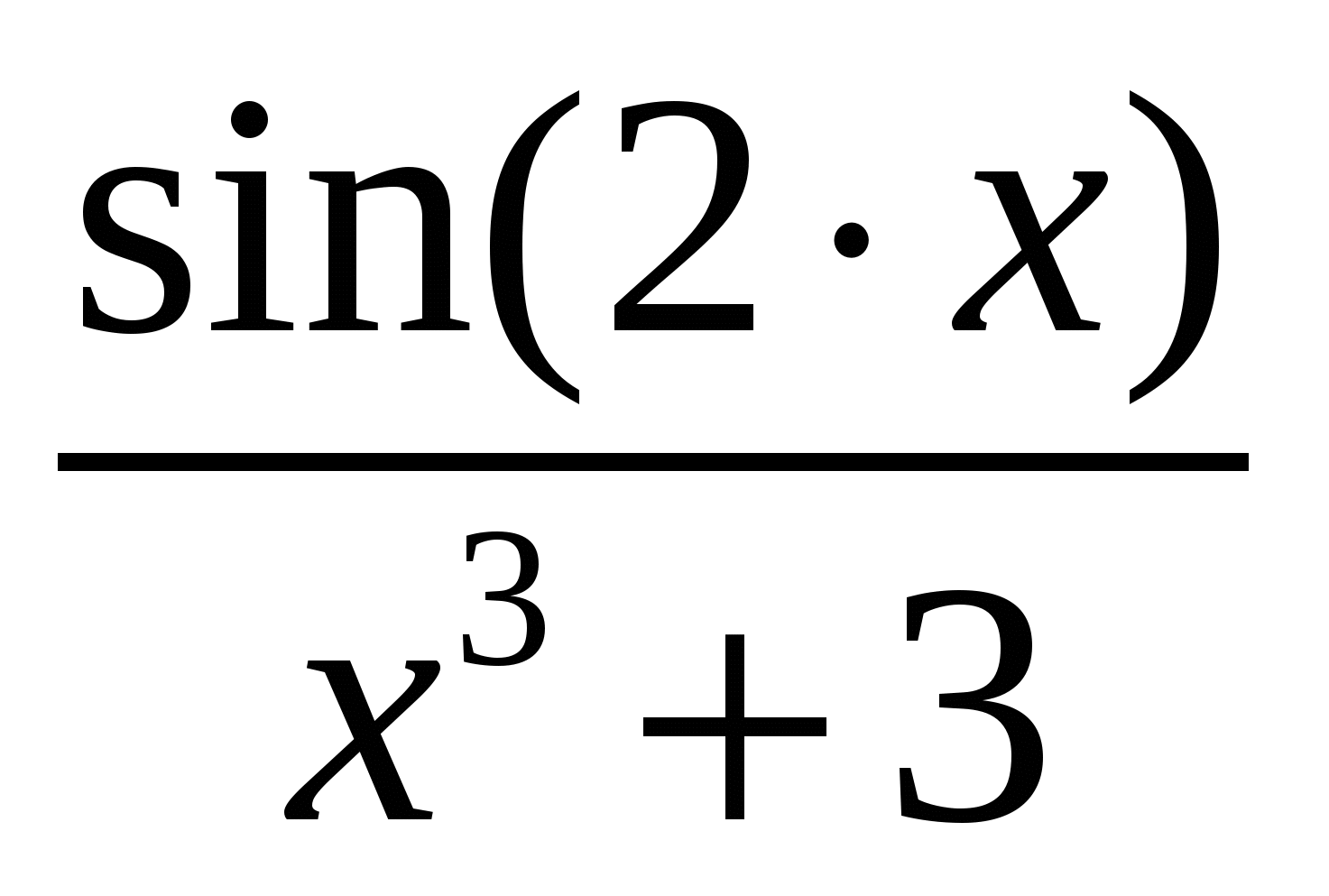
|
5
|
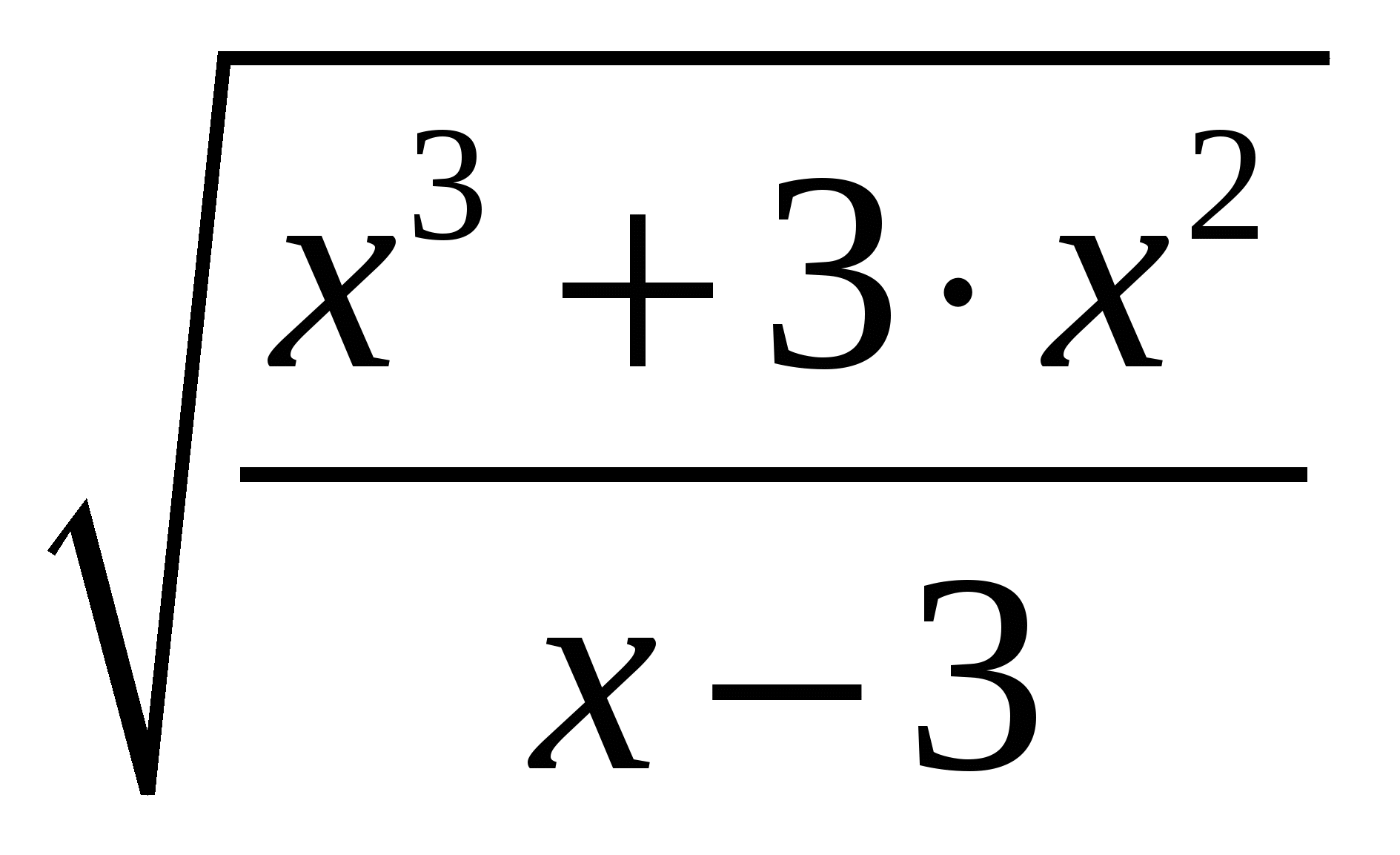
|
18
|
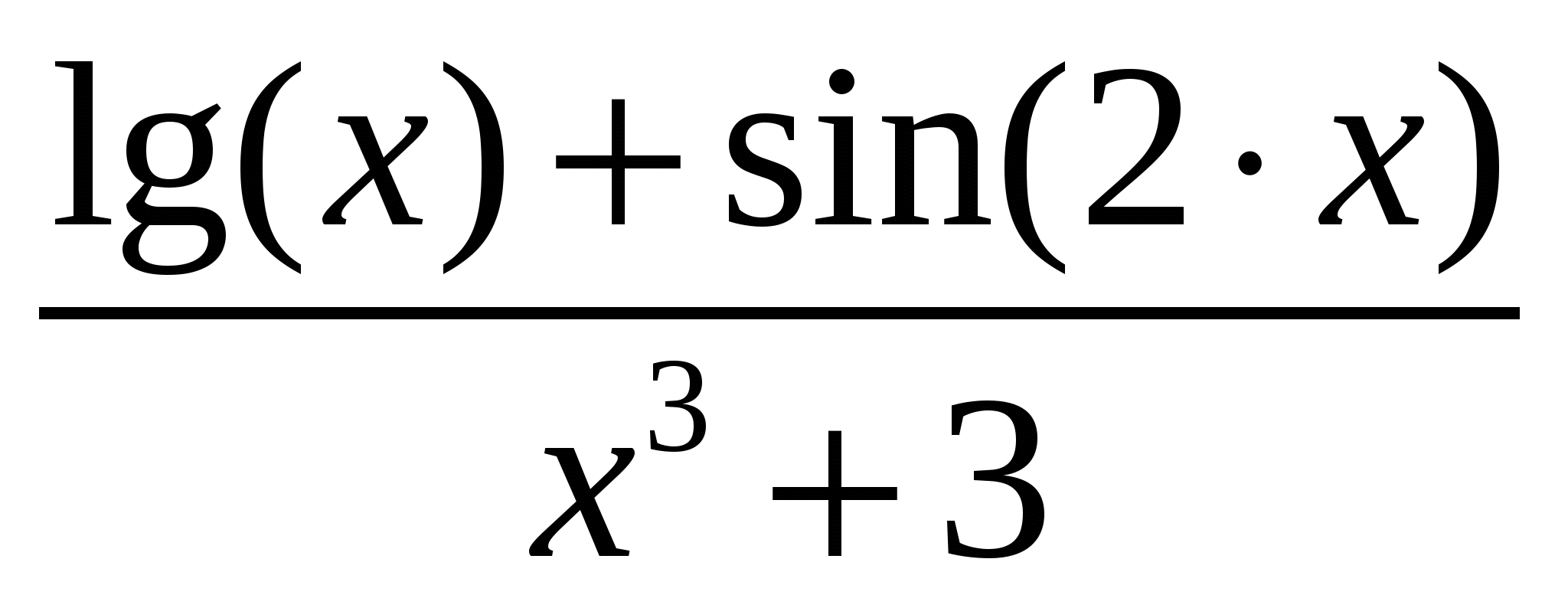
|
6
|
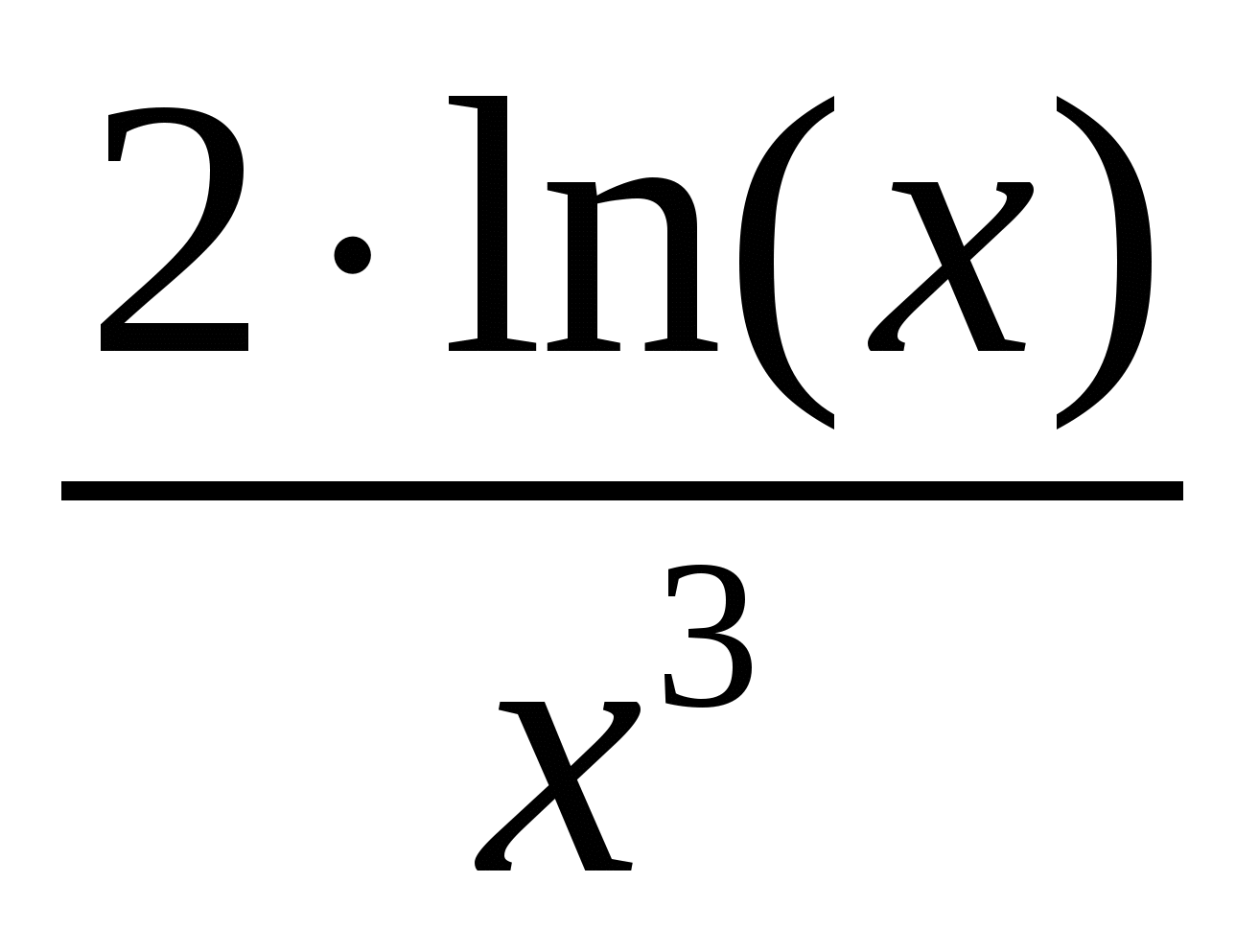
|
19
|
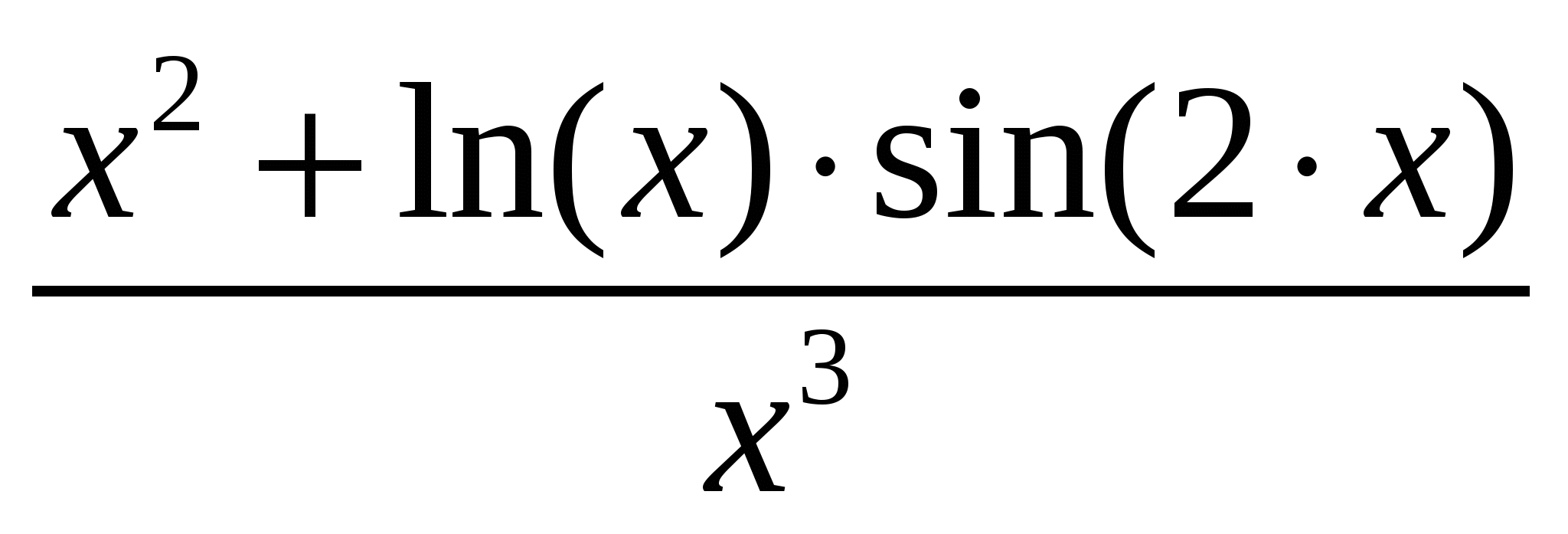
|
7
|
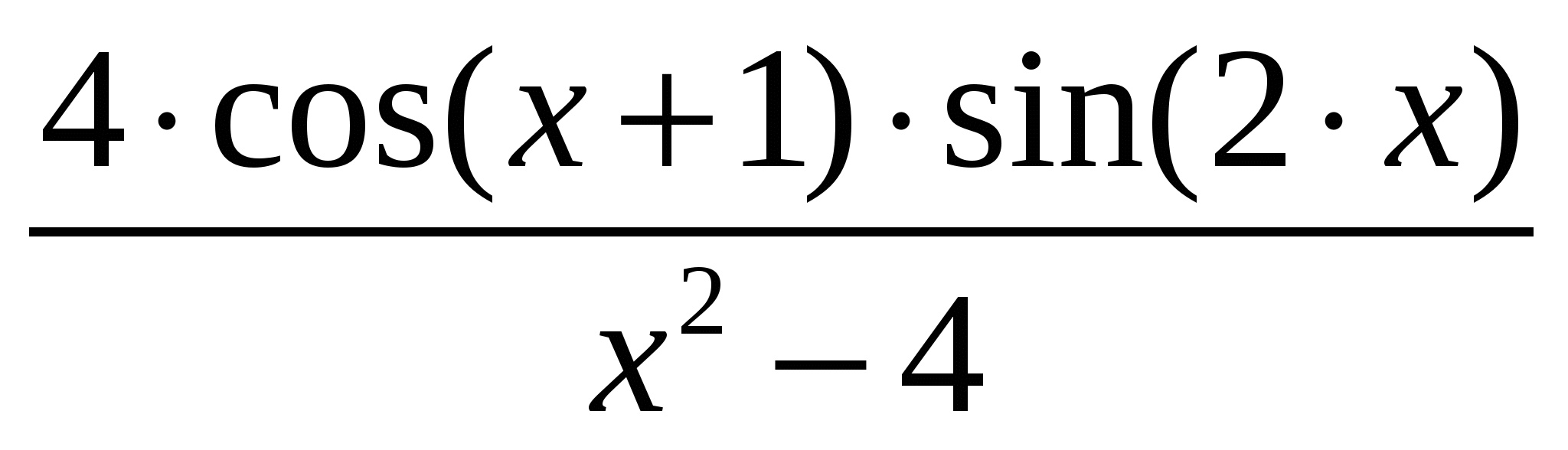
|
20
|
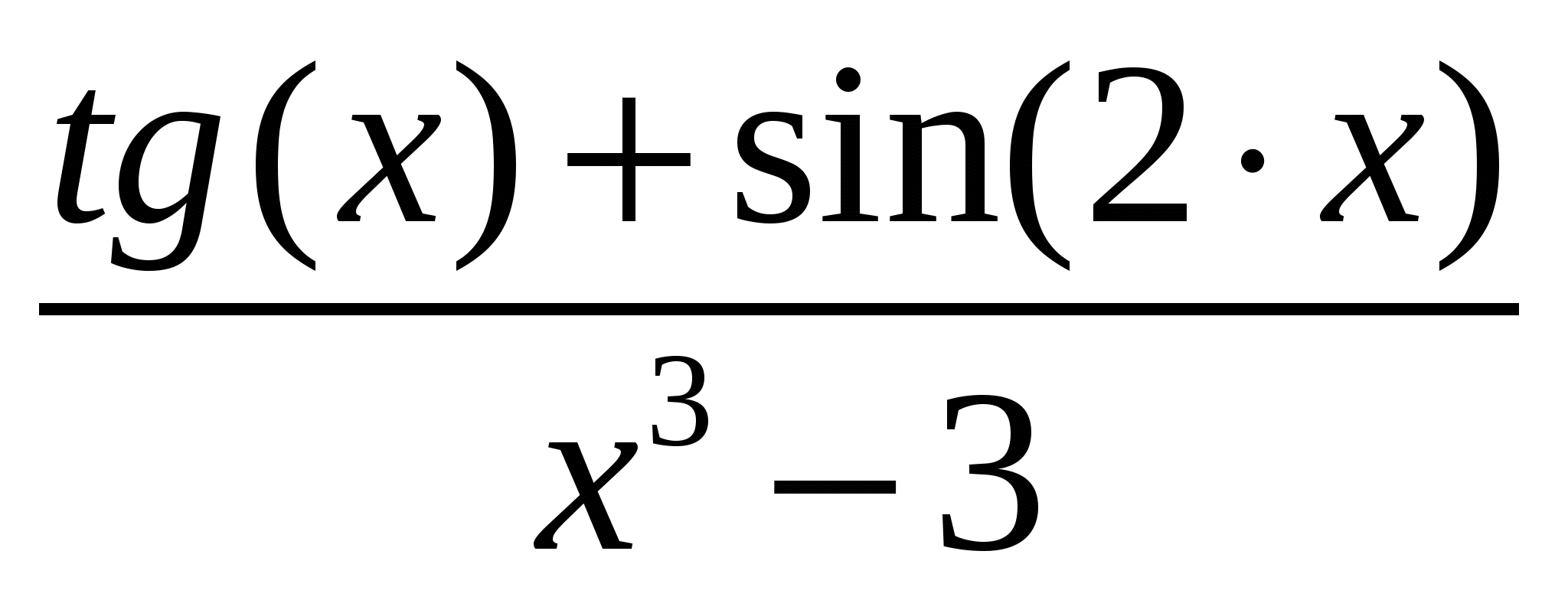
|
8
|
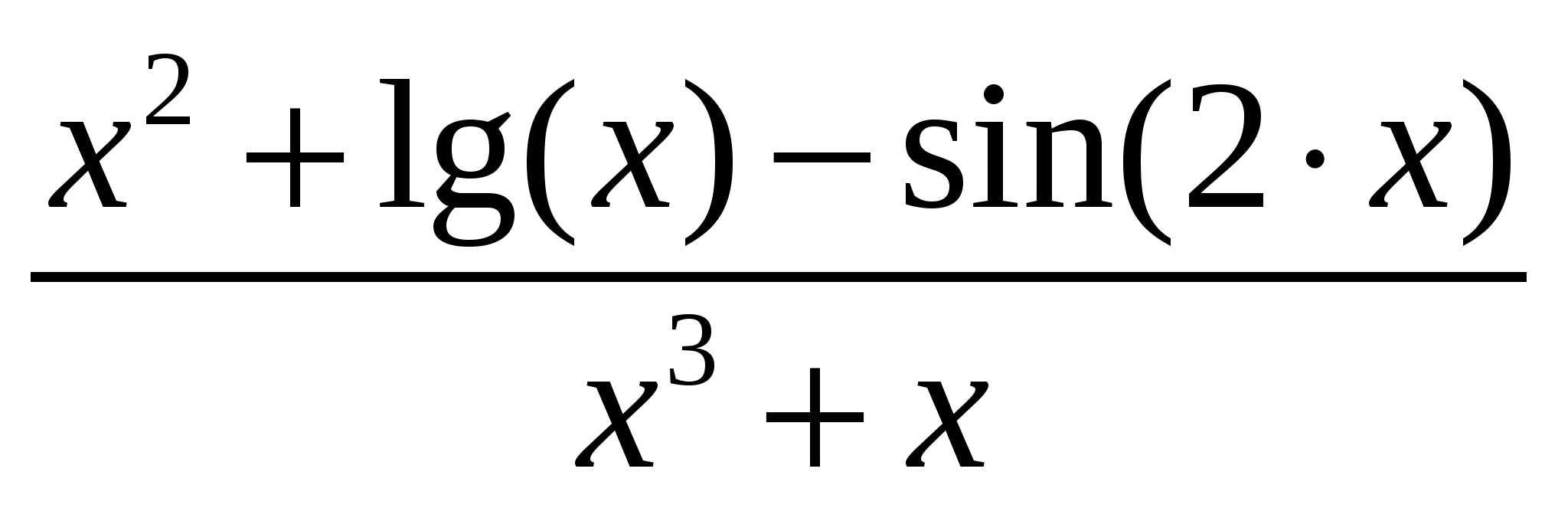
|
21
|
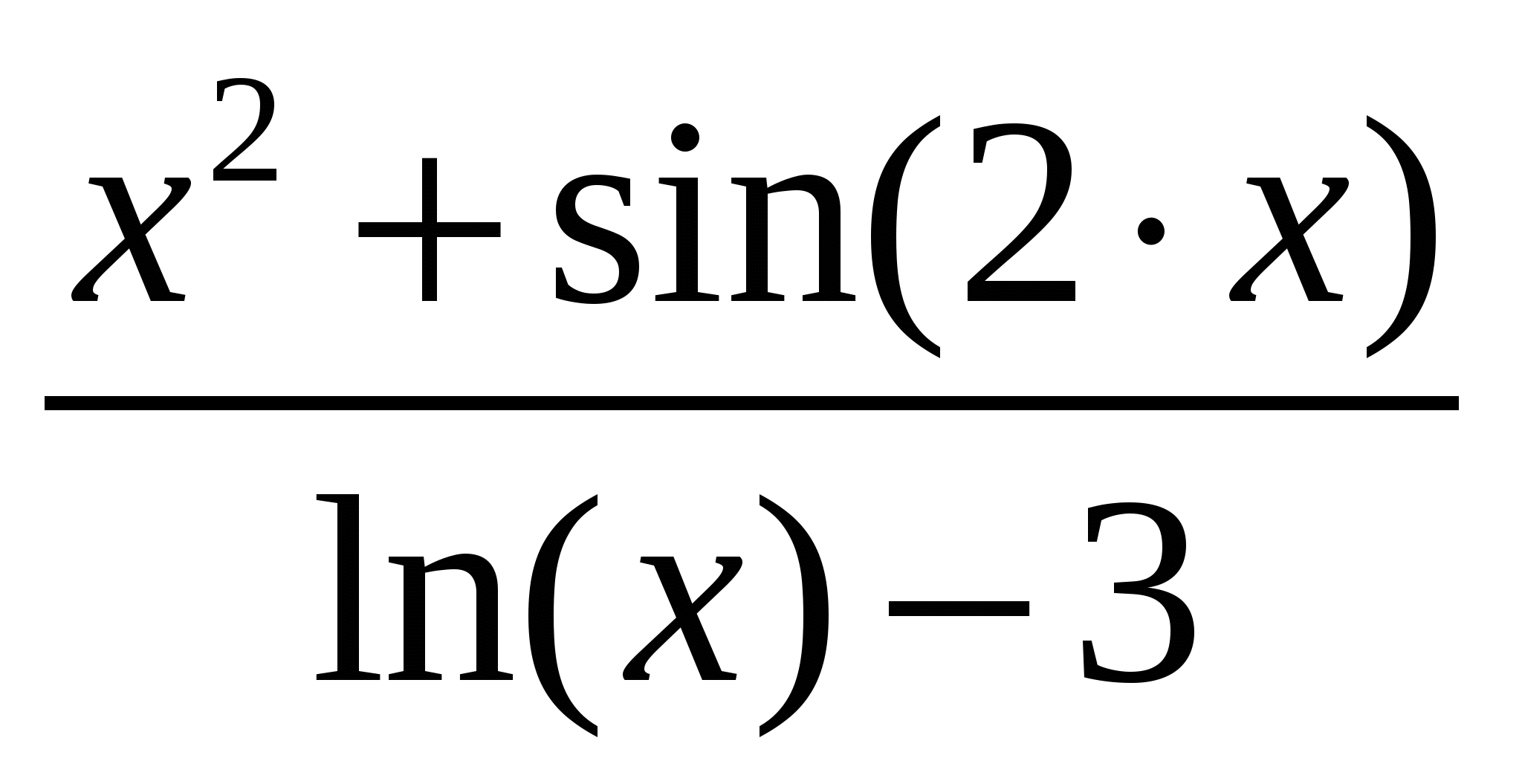
|
9
|
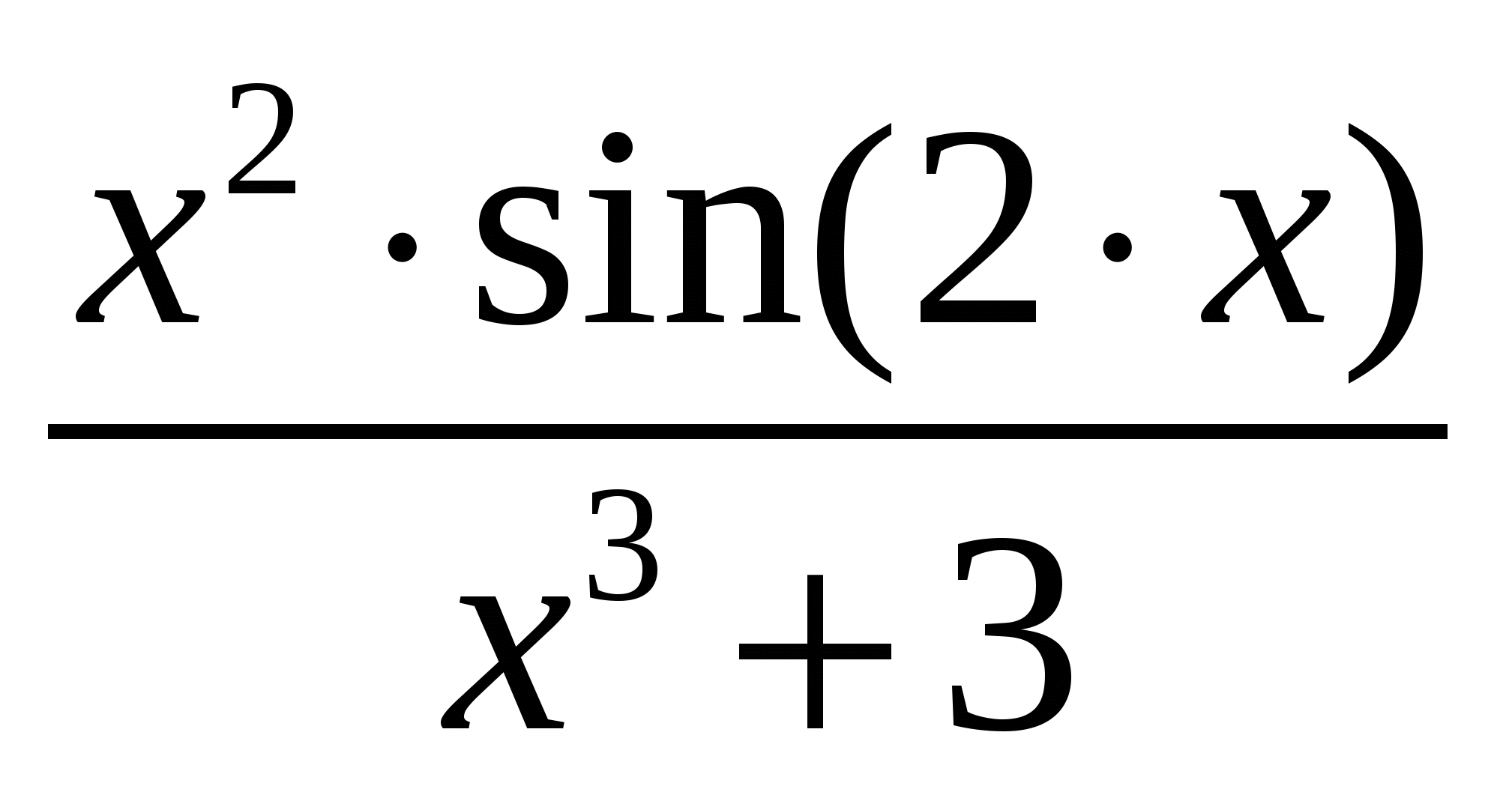
|
22
|
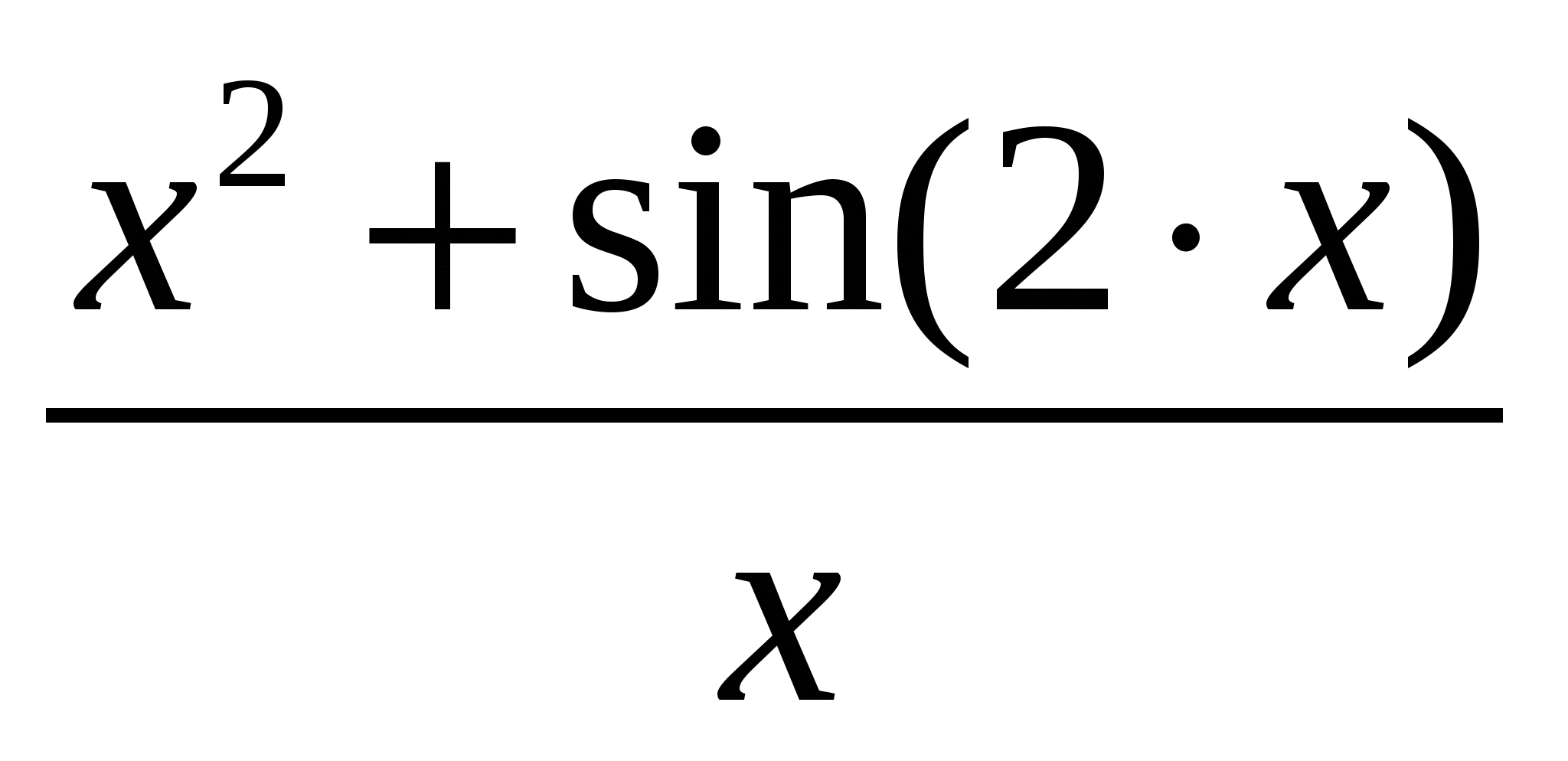
|
10
|
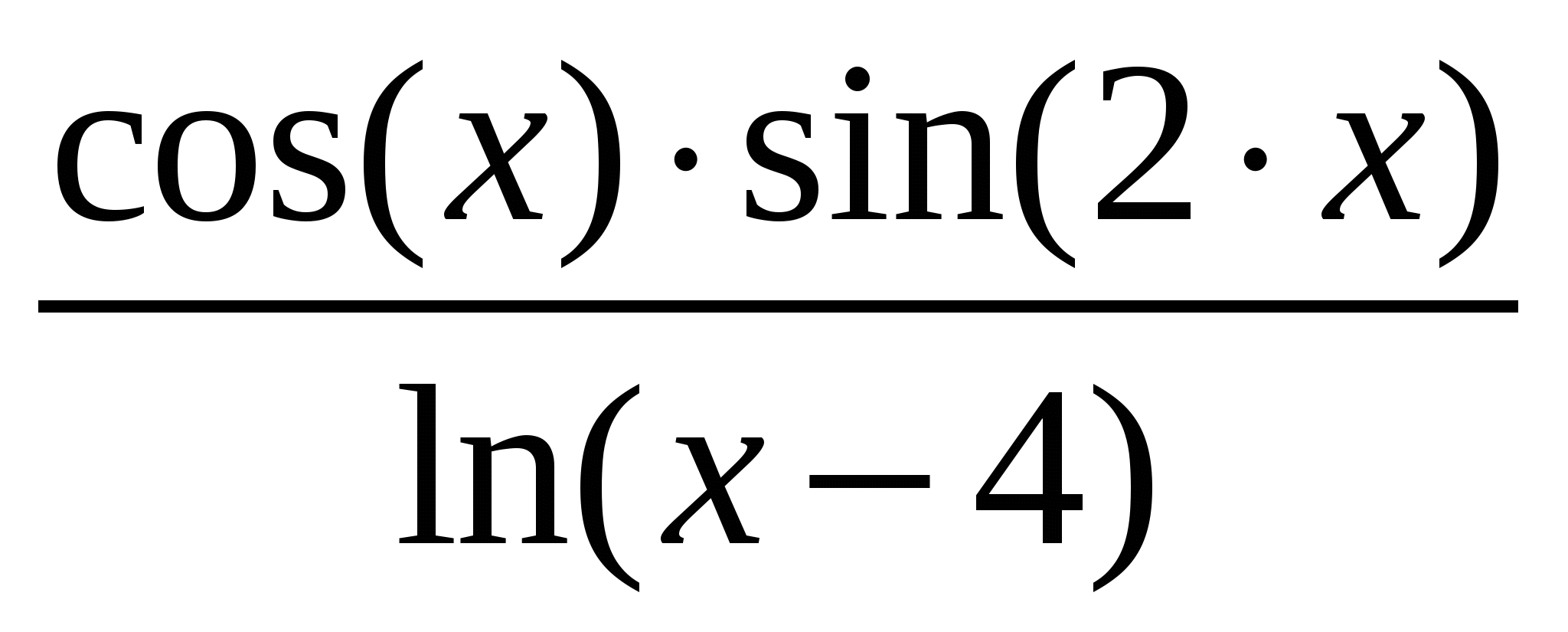
|
23
|
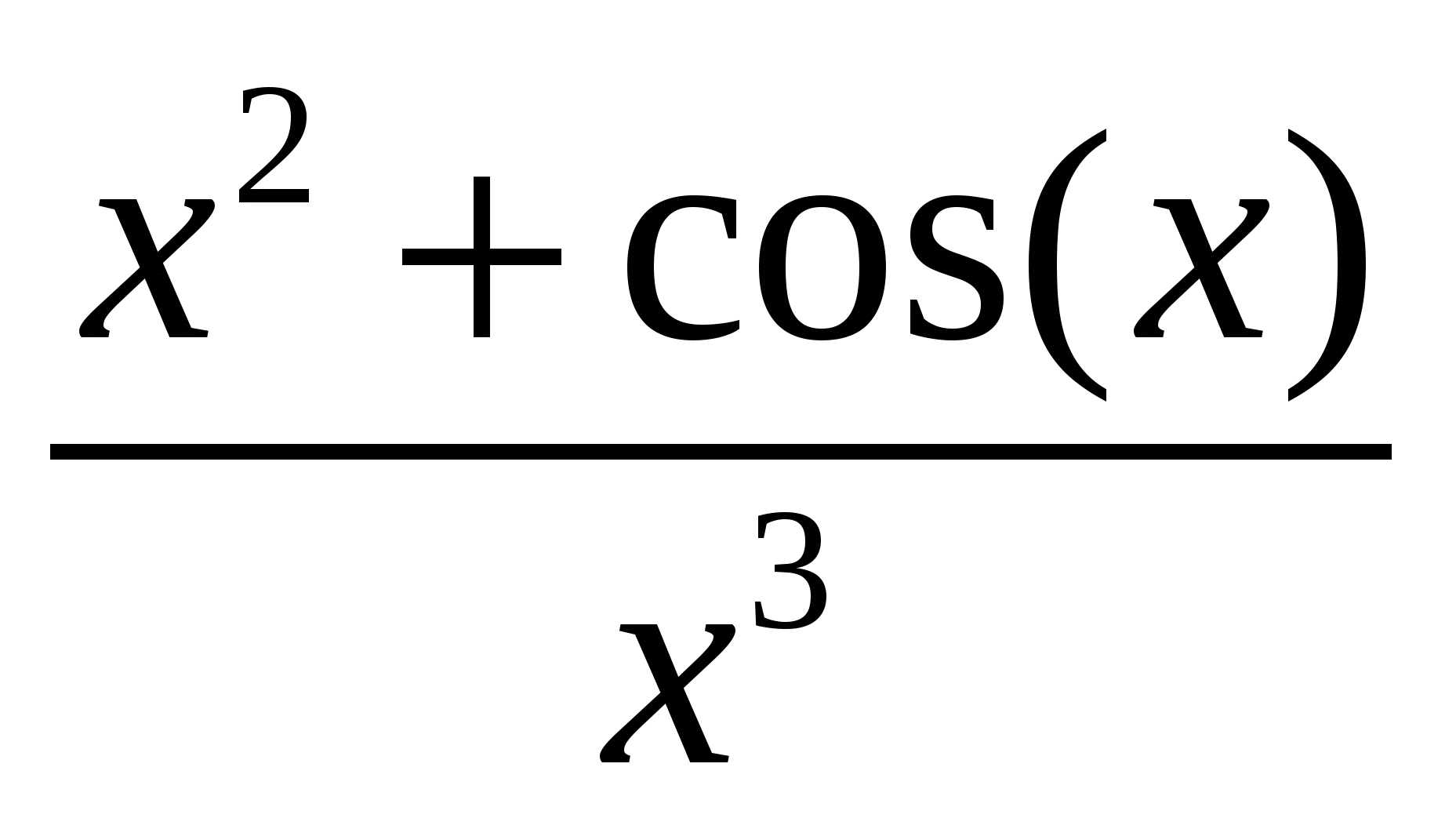
|
11
|
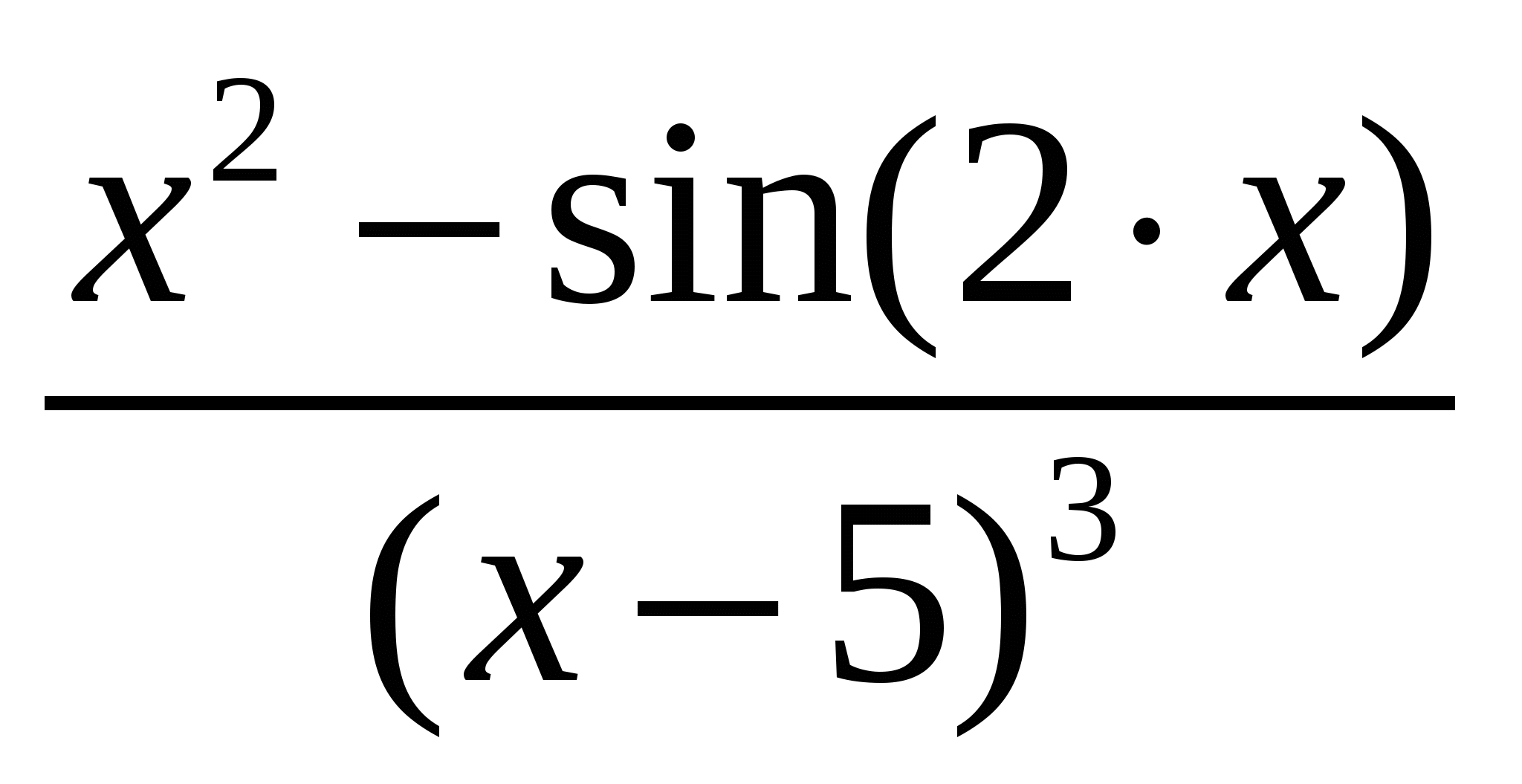
|
24
|
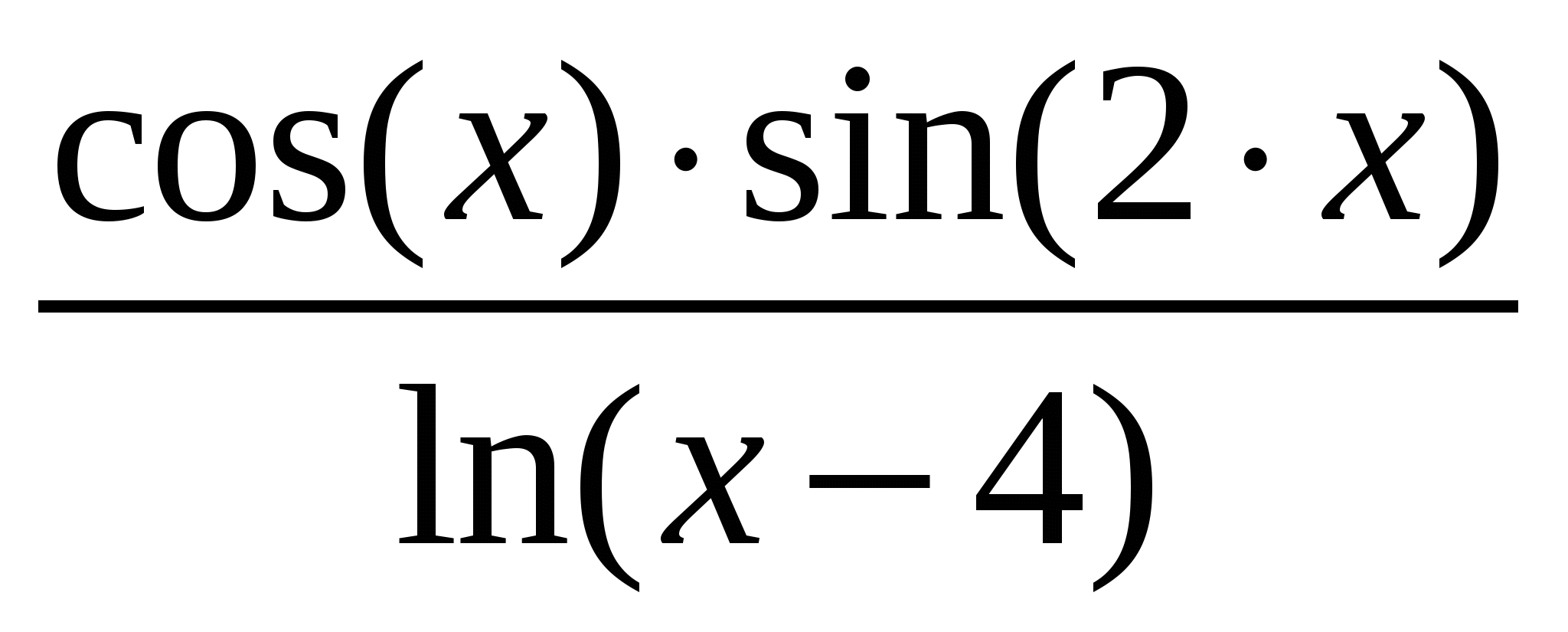
|
12
|
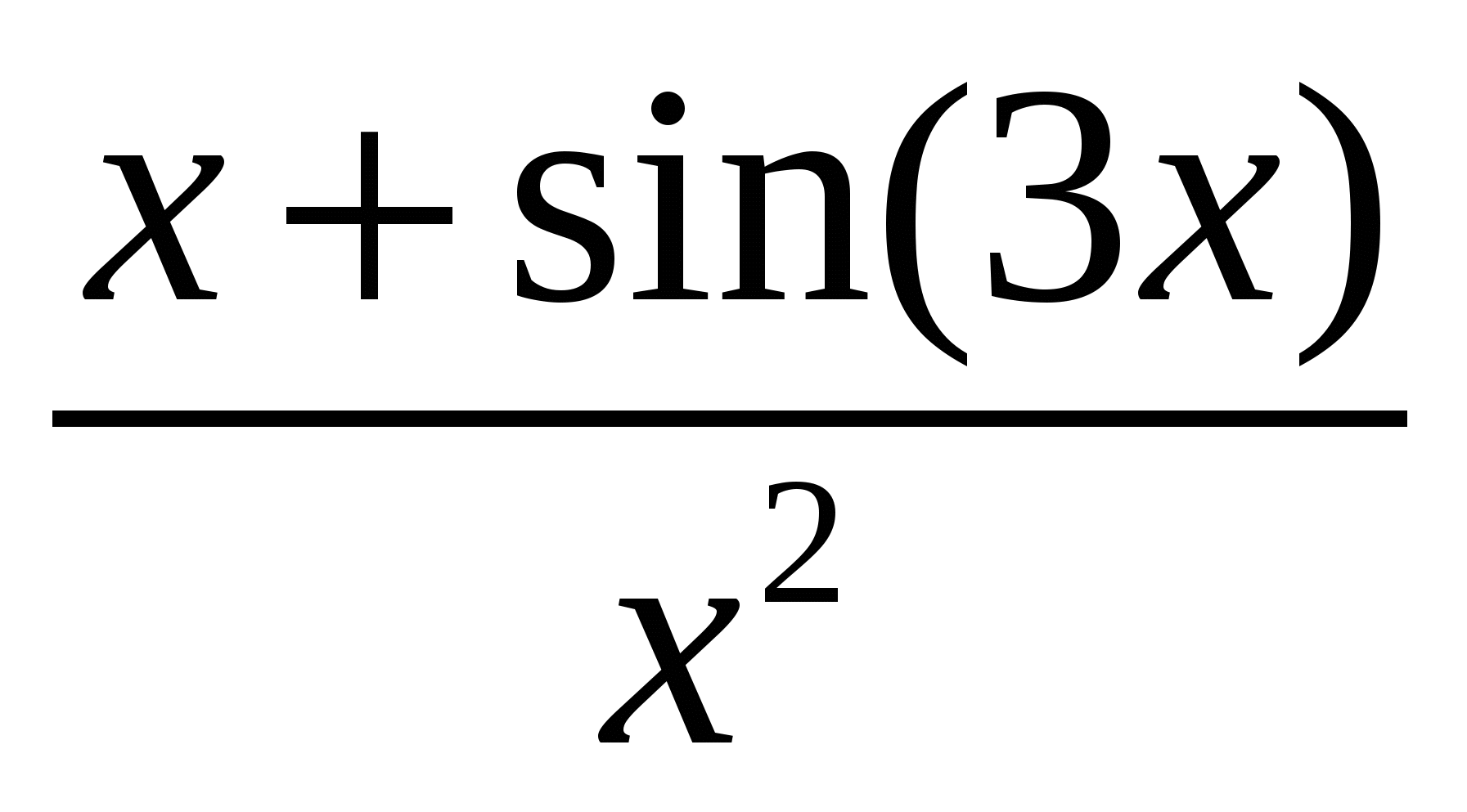
|
25
|
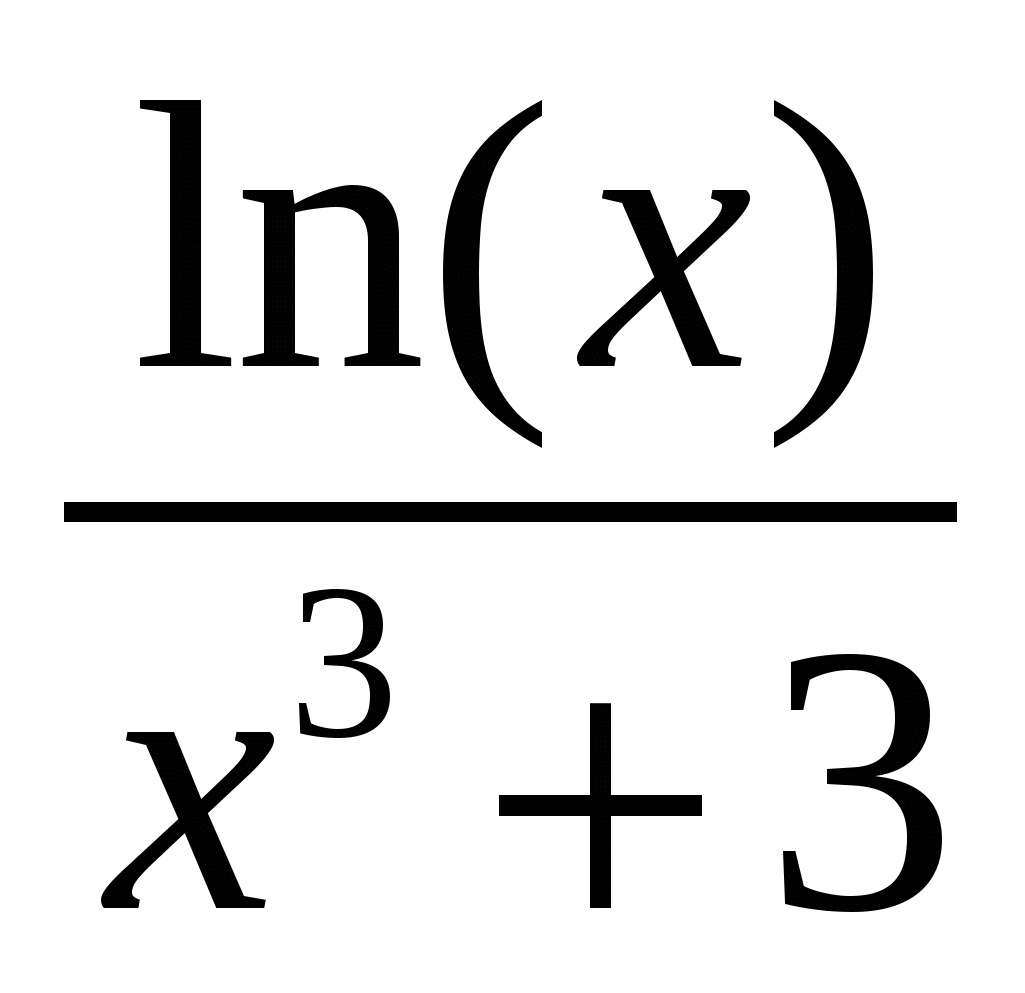
|
13
|
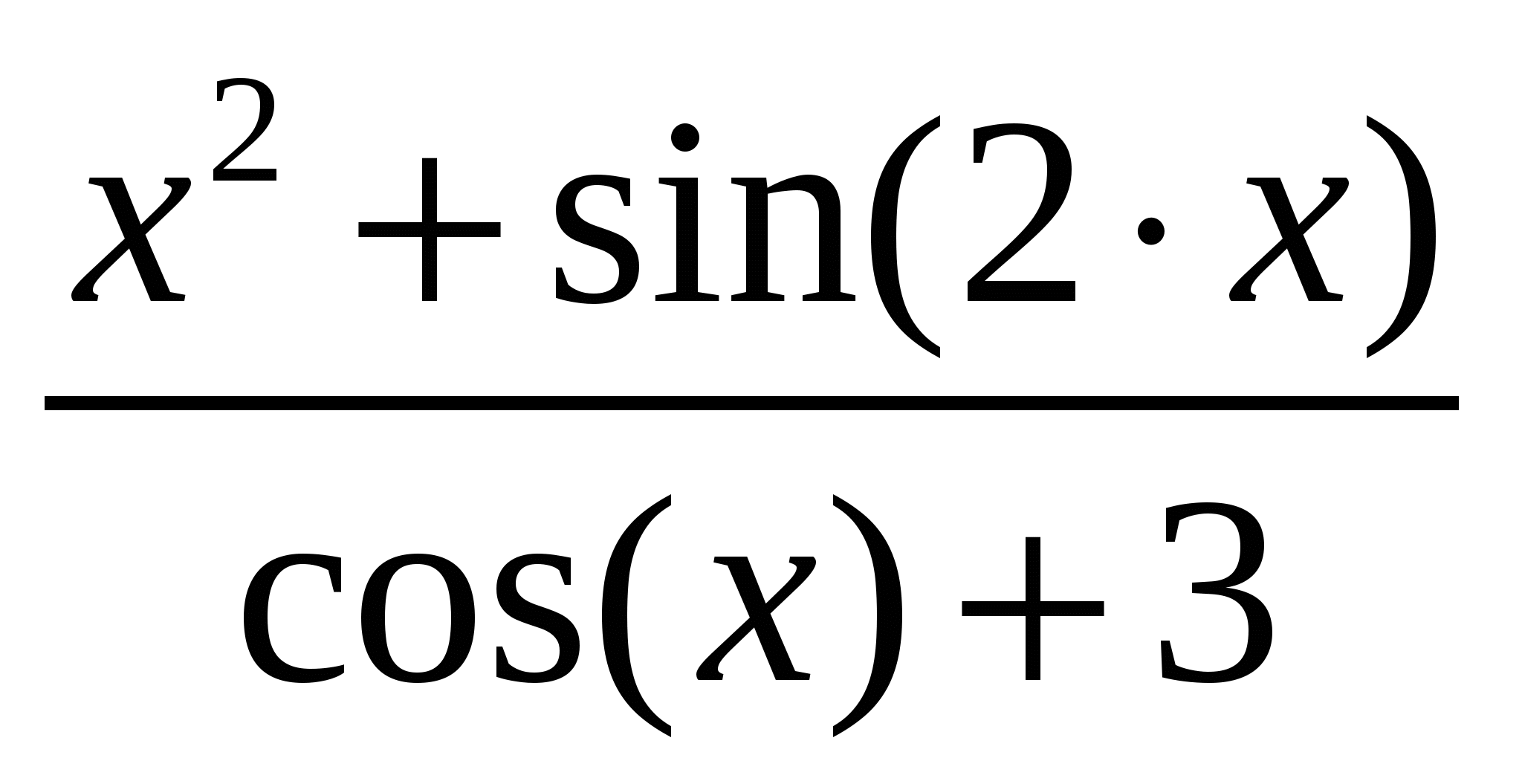
|
|
|
Контрольные вопросы
Какие уравнения называют алгебраическими, а какие трансцендентными? Что такое корень уравнения?
Этапы численного решения алгебраических и трансцендентных уравнений.
Опишите табличный способ отделения корней уравнения.
В каких случаях применяются численные методы для решения алгебраических и трансцендентных уравнений?
Объясните суть метода половинного деления. Приведите условие окончания вычислительной процедуры.
Составьте блок-схему алгоритма решения алгебраического уравнения методом половинного деления.
Объясните суть метода Ньютона. Приведите условие окончания вычислительной процедуры.
Выведите соотношение для расчета очередного приближения к корню уравнения согласно методу Ньютона.
В чем отличие модифицированного метода Ньютона от искомого?
Объясните суть метода секущих. Приведите условие окончания вычислительной процедуры.
Выведите соотношение для расчета очередного приближения к корню уравнения согласно методу секущих.
Какие системы алгебраических уравнений называют линейными?
В каких случаях применяют численные методы для решения СЛАУ?
Почему реализация метода Гаусса на ЭВМ дает решения с ошибкой, хотя метод Гаусса относят к группе точных? Как можно бы было уменьшить ошибку решения?
В чем отличие метода Зейделя от метода итераций?
Поясните процедуру прямого и обратного хода метода Гаусса.
Какому условию должна удовлетворять система, чтобы ее можно было решить методом Гаусса?
Сформулируйте необходимое условие сходимости итерационного процесса для методов итераций и Зейделя.
В каких случаях, по вашему мнению, следует применять прямые численные методы решения СЛАУ, а в каких – итерационные? По каким критериям Вы будете осуществлять выбор метода для решения конкретной СЛАУ?
Дайте понятие аппроксимации функции. В каких случаях прибегают к методам аппроксимации.
Раскройте сущность метода восстановления функции – интерполяция.
Какому условию должны удовлетворять интерполяционные полиномы?
Изобразите графически процедуру интерполирования функции.
Как должны соотноситься порядок интерполяционного полинома и число узлов интерполирования?
Приведите общий вид математического описания полинома Лагранжа.
Что собою представляет полином Лагранжа 0-степени?
Что получается в результате вычислительной процедуры по формуле Лагранжа?
В каких случаях прибегают к численным методам расчета определенных интегралов?
Поясните общую суть методов численного интегрирования, использующих квадратурные формулы.
Какой порядок имеет степенные полиномы, с помощью которых аппроксимируют подынтегральную функцию в методах прямоугольников, трапеций и Симпсона?
Выведите формулу для расчета определенного интеграла методом правых, левых и средних прямоугольников.
Выведите формулу для расчета определенного интеграла методом трапеций.
Выведите формулу для расчета определенного интеграла методом Симпсона.
Как можно оценить точность интегрирования методами прямоугольников, трапеций и Симпсона?
Как можно повысить точность вычисления определенного интеграла методами, использующими квадратурные формулы?
|
|
|
 Скачать 0.72 Mb.
Скачать 0.72 Mb.