Практикум по напорной гидравлике и гидромашинам учебное пособие

• Название: Практикум по напорной гидравлике и гидромашинам учебное пособие
• Дата: 31.03.2023
• Размер: 4.09 Mb.
• Имя файла: virtualnyj-laboratornyj-praktikum_color.docx
• Тип: Практикум; #1027990
• страница: 16 из 31

Виртуальная лабораторная работа № 6 ИЗУЧЕНИЕ ИСТЕЧЕНИЯ ЖИДКОСТИ

ЧЕРЕЗ МАЛЫЕ ОТВЕРСТИЯ В ТОНКОЙ СТЕНКЕ

И НАСАДКИ ПРИ ПОСТОЯННОМ НАПОРЕ В АТМОСФЕРУ
Вводная часть

Малым считается отверстие, линейный размер которого не превышает 0,1Н (рис. 12), где Н – превышение свободной поверхности жидкости над центром тяжести отверстия.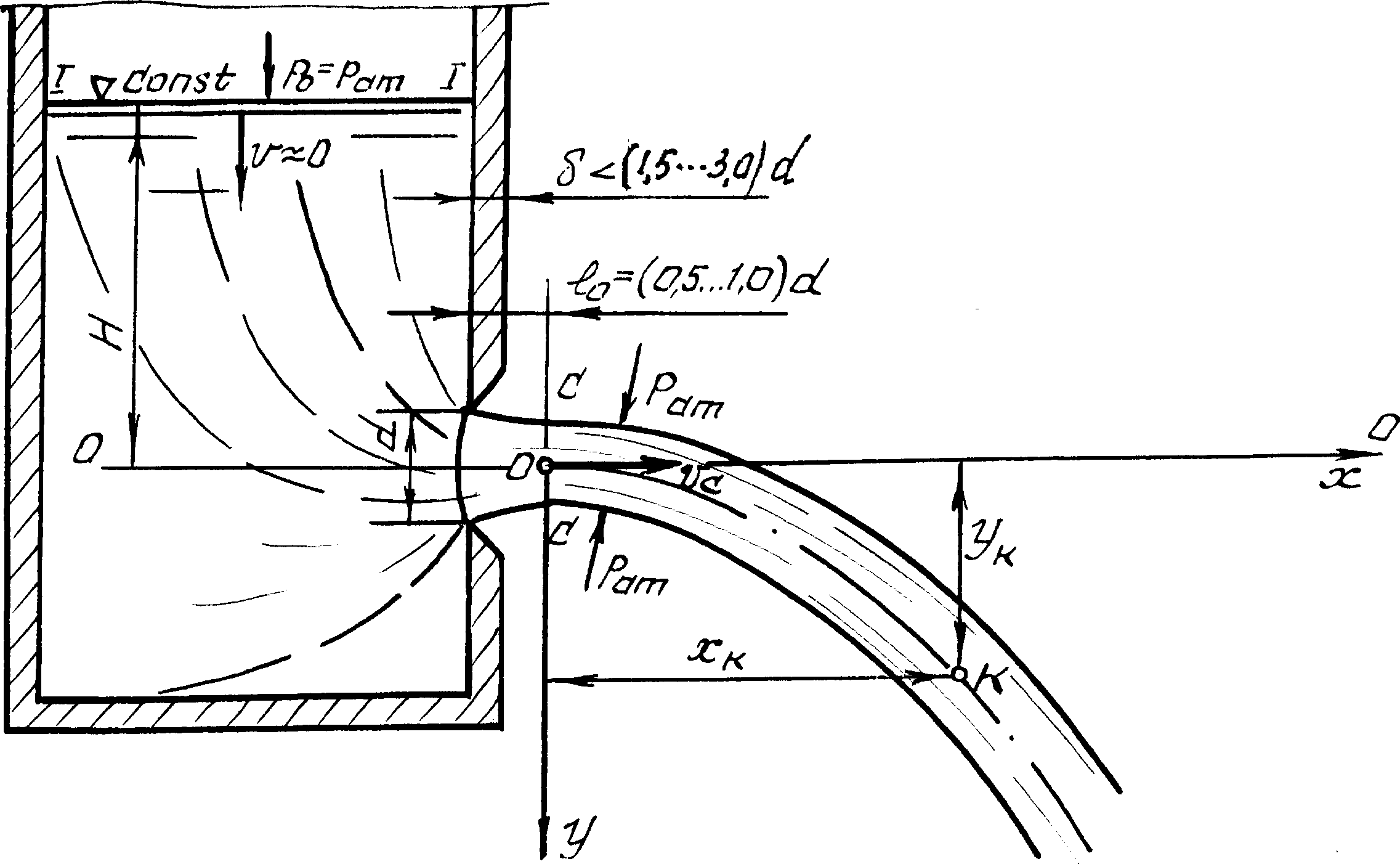



Рис. 12. Истечение жидкости из малого отверстия в тонкой стенке в атмосферу
Стенку считают тонкой, если ее толщина  < (1,5...3,0)d (см. рис. 12). При выполнении этого условия величина  не влияет на характер истечения жидкости из отверстия, так как вытекающая струя жидкости касается только острой кромки отверстия [2, 5, 9].

Поскольку частицы жидкости движутся к отверстию по криволинейным траекториям, то за счет сил инерции струя, вытекающая из отверстия, сжимается. Благодаря действию сил инерции струя продолжает сжиматься и после выхода из отверстия. Наибольшее сжатие струи, как показывают опыты, наблюдается в сечении С–С на расстоянии примерно (0,5...1,0)d от входной кромки отверстия (см. рис. 12). Это сечение называют сжатым. Степень сжатия струи в этом сечении оценивают величиной коэффициента сжатия ε:

𝜀 = ^𝑆с , (23)

𝑆

где S_с и S – площадь сжатого живого сечения струи и площадь отверстия соответственно.


Среднюю скорость струи ʋ_с в сжатом сечении С–С при р₀ = р_ат вычисляют по формуле, полученной из уравнения Д. Бернулли, составленного для сечений I–I и С–С (см. рис. 12):

^{𝑣𝑐 = 𝜑 2𝑔𝐻 , (24)}

где – коэффициент скорости отверстия, определяемый по формуле

𝜑 = <sup>1

𝛼+</sup>

_≈ 1

^1+

, (25)

где α – коэффициент Кориолиса (корректив кинетической энергии);

ζ – коэффициент местного сопротивления отверстия.

Исходя из уравнения траектории струи, вытекающей из отверстия, получено еще одно выражение для коэффициента :

𝜑 = <sup>𝑥𝑖

2 𝑦</sup>_𝑖 ^𝐻

, (26)

где x_i и y_i – координаты произвольно взятой точки траектории струи.

Поскольку напор теряется главным образом вблизи отверстия, где скорости достаточно велики, при истечении из отверстия во внимание принимают только местные потери напора.


Расход жидкости Q через отверстие вычисляют так:

^{𝑄 = 𝜑𝜀𝑆 2𝑔𝐻 . (27)}

Введя обозначение получим
𝜑𝜀 = 𝜇 , (28)





^{𝑄 = 𝜇𝑆 2𝑔𝐻 , (29)}

где μ – коэффициент расхода отверстия, учитывающий влияние гидравлического сопротивления и сжатия струи на расход жидкости.

Величины коэффициентов , , , для отверстий определяют опытным путем. Установлено, что они зависят от формы отверстия и числа Рейнольдса. Однако при больших числах Рейнольдса Re  10⁵ указанные коэффициенты от Re не зависят и для круглых и квадратных отверстий при совершенном сжатии струи равны: = 0,62...0,64; = 0,06;

 = 0,97...0,98; = 0,60...0,62.

Насадком называют патрубок длиной 2,5d  L_H  5d (рис. 13), присоединенный к малому отверстию в тонкой стенке с целью изменения гидравлических характеристик истечения (скорости, расхода жидкости, траектории струи) [14, 15].

Насадки бывают цилиндрические (внешние и внутренние), конические (сходящиеся и расходящиеся) и коноидальные, т. е. очерченные по форме струи, вытекающей из отверстия.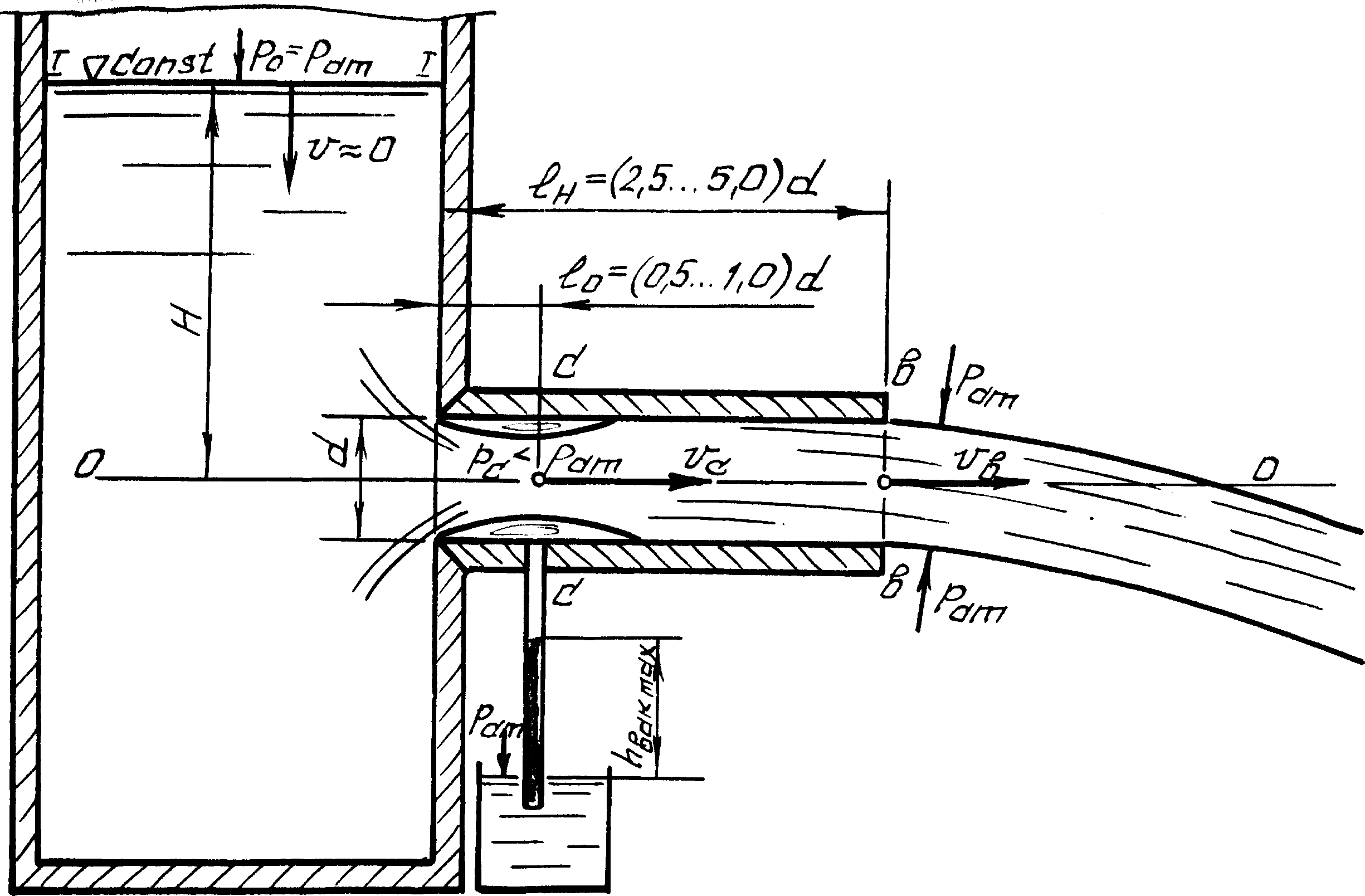

Использование насадка любого типа вызывает увеличение расхода жидкости Q благодаря вакууму, возникающему внутри насадка в области сжатого сечения С–С (рис. 13) и обусловливающему повышение напора истечения.

Рис. 13. Истечение жидкости из внешнего цилиндрического насадка в атмосферу

Среднюю скорость истечения жидкости из насадка ʋ и расход Q определяют по формулам, полученным из уравнения Д. Бернулли, записываемого для сечений I–I и в–в (см. рис. 13):

^{𝑣 = 𝜑н 2𝑔𝐻 , (30)}

где φ_н – коэффициент скорости насадка:

н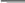
𝜑 = ¹

𝛼+_н

, (31)

где ζ_н – коэффициент сопротивления насадка.

Для выходного сечения в–в коэффициент сжатия струи = 1, так как насадок здесь работает полным сечением. Поэтому коэффициент расхода насадка _н = _н.


Расход жидкости, вытекающей из насадка, вычисляется по формуле, аналогичной формуле (29):

^{𝑄 = 𝜇н𝑆 2𝑔𝐻 . (32)}