Финансовая граммотность. Практикум по решению задач по теме Фондовый рынок его значение для увеличения личных доходов
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Выполнила: студентка группы СлБДв-211гд Искорнева Аида Камильевна Практикум по решению задач по теме «Фондовый рынок: его значение для увеличения личных доходов» Вклады, кредиты Формулы: Начисление простых процентов: Начисление сложных процентов с ежегодным начислением: где Р – начальная сумма вклада; n- лет ( срок вклада с ежегодным начислением процентов); r – процентная ставка годовых Начисление сложных процентов m раз в год : m – месяцев (кварталов) с ежемесячным (ежеквартальным) начислением процентов Задача 1. Вкладчик вложил 100000 руб. при простой ставке 3% годовых. Какая сумма будет на лицевом счете через 5 лет; 8 лет; 10 лет ? Решение. В данной задаче необходимо вычислить А, если P=100000 рублей, I=3%=0,03, T=5;8;10 лет. Подставим данные в формулу, получим А=100000*(1+0,03*5)=115000 рублей. Аналогично, вычислим для Т=8 и 10 лет. А=100000*(1+0,03*8)=124000 рублей. А=100000*(1+0,03*10)=130000 рублей. Ответ. Через 5 лет на лицевом счету вкладчика будет 115000 рублей, через 8 лет- 124000 рублей, через 10 лет - 130000 рублей. Задача 2. За 4 месяца при простой ставке 9% в год на счете у вкладчика стало 500 тыс. руб. Сколько он вложил в банк? Решение. 9% годовых=9/12=0,75% в месяц. В данной задаче необходимо найти P, зная, что А=500, I=0,0075, T=4 месяца. Подставим в формулу, получим уравнение: 500=Р*(1+4*0,0075), отсюда получим выражение для нахождения Р=500/(1+4*0,0075)=384,6 тыс. руб. Ответ. Вкладчик положил в банк 384,6 тыс. руб Задача 3 HYPERLINK "http://finansovaya-matematika.5311pro2.edusite.ru/p54aa1.html" HYPERLINK "http://finansovaya-matematika.5311pro2.edusite.ru/p54aa1.html" HYPERLINK "http://finansovaya-matematika.5311pro2.edusite.ru/p54aa1.html". HYPERLINK "http://finansovaya-matematika.5311pro2.edusite.ru/p54aa1.html"Вкладчик положил в банк 65000 рублей под 6% годовых (сложная процентная ставка). Какую сумму он получит через 10 лет Решение. Рассмотрим известные данные к задаче. A=65000, T=10, R=6%=0,06. Подставим данные в формулу, вычислим S(должна быть равной 100000 или больше). S=65000*(1+0,06)10 S=65000*1,06 10 S=65000*1,79 S=116405 Задача 4. Определите результат вложения 500000 руб. на 3 года путем открытия банковского вклада по ставке 4,7 % (сложные проценты). Решение. В этой задаче исходными данными являются: A=50000, T=3 года, R=10%=0,047. Подставим эти данные в формулу, получим S=50000*(1+0,047)3=50000*1,141=57050 рублей. Ответ. На счету через три года будет 57050 рублей. Задача 5. Рассчитать сумму, которую получит вкладчик через 3 года при ежемесячном начислении сложных процентов и ставке 10% годовых, если было вложено 100000 рублей. Решение: В этой задаче исходными данными являются: A=100000, T=3 года, R=10%=0,1. Подставим эти данные в формулу, получим S=100000*(1+0,1)3=100000*1,13=100000*1,331=133100 рублей. Ответ. На счету через три года будет 133100 рублей. Задача 6. Кредитная организация принимает вклады по простой ставке 5,8 % годовых. Определите сумму процентов на вклад 200 000 рублей, размещённый на 3 года при ежеквартальном начислении процентов. Решение:Сумма процентных денег находится по формуле: I=D×i×n где: D-сумма вклада, i – ставка %, n-срок в годах, I=200000×0,058×2= 23200 руб. Ответ: 23200 руб Задача 7. Кредит для покупки дома выдан на сумму 4 000 000 рублей сроком на 5 лет. Процентная ставка составляет 14 % годовых. Погашение кредита производится в конце каждого месяца. Определить сумму, которая должна быть выплачена за все пять лет. Решение:Эта задача решается по формуле сложных процентов с начислением процентов несколько раз в году: ( n – срок кредита, m – число выплат в год) Тогда, E=46*10(1+0,14:12)12*5= 8,022×106 Ответ: сумма, которая должна быть выплачена за все пять лет равна 8,022×106 рублей Задача 8. Банк предлагает на выбор два вклада: «Первый» (ставка 8 % годовых, проценты начисляются ежеквартально по методу простых процентов) и «Второй» (ставка 7,8 % годовых, проценты начисляются ежемесячно по методу сложных процентов). Сумма вклада 100 000 руб. Какой вклад позволит получить больший доход: а) «Первый»; б) «Второй»; в) одинаково; г) для точного ответа не хватает данных. Задача 9. Какой депозит для вас будет более выгодным: а) на 9 месяцев с фиксированной ставкой 6,5 % (без капитализации (простой процент)); б) на 9 месяцев с фиксированной ставкой 6,2 % (с ежемесячной капитализацией процентов). Доходность акций Акция может приносить доход двумя способами. Во-первых, в форме дивидендов. Являясь держателем (владельцем) ценной бумаги, инвестор может рассчитывать на получение дивиденда по акциям. (Общество не обязано платить дивиденды по обыкновенным акциям). Во-вторых, можно добиться прироста капитала, который выражается разницей между ценой покупки и ценой, по которой инвестор продает акцию. В общем виде доходность является относительным показателем и представляет собой доход, приходящийся на единицу затрат. Различают дивидендную доходность и полную (конечную) доходность акций. Показатель текущей доходности характеризует годовые (текущие) поступления от акции относительно сделанных затрат на ее покупку. Дивидендная доходность. Дивидендная доходность определяется делением общей суммы дивидендов на акцию за год на текущую рыночную цену акции (или цену покупки). 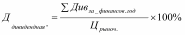 Однако, поскольку этим способом можно измерить только то, что уже имело место, и необязательно, что это будет показателем будущих дивидендов. Полная (конечная) доходность. Если инвестиционный период, по которому оцениваются акции, включает выплату дивидендов и заканчивается их реализацией, то доход определяется как совокупные дивиденды с учетом изменения курсовой стоимости Формула конечной доходности имеет следующий вид: 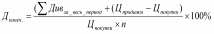 n - период владения акцией в годах*. ______________________________________ *если период владения активом меньше года, то месяцы (дни) переводим в года: n= 6 мес./12 мес; n= 3 мес./12 мес.; 100 дн./365дн. и т.д. Задача 1. Инвестор приобрел акцию стоимостью 130 рублей и продал ее через три года. Дивиденды за каждый год выплачивались в размере 13 руб. Определить конечную доходность акции для инвестора, если известно, что цена продажи акции составила 252 руб. Решение:dk = ((Ps - Pb)/ n + D)/Pb × 100 %,= ((252-130)/3 + 13)/130*100% = 41% Ps сумма продажи акции-252 Pb сумма покупки акции-130 D диведенты n-количество лет Ответ:конечная доходность акции 41% Задача 2. Инвестор купил 100 акций по цене 300 руб., через 4 года акции были проданы по цене 450 руб. За это время инвестор получил дивиденды в размере 20, 25, 30, 35 руб. на акцию. Определите доходность операции инвестора. Решение : 1) Сумма покупки акций Пок. ак. = 100*300 = 30000 руб. 2) Сумма продажи акций Пр. ак. = 100*450 = 45000 руб. 3) Сумма полученных дивидендов Д 3 года = 100*300*(0,2+0,25+0,3+0,35) = 33000 руб. 4) Общий доход равен 45000+33000-30000 = 48000 руб. 5) Дох-сть48000/30000*100%=16% Задача 3. Инвестор приобрел привилегированную акцию с фиксированным размером дивиденда по рыночному курсу. Через пять лет акция была продана. В течение этих лет регулярно выплачивались дивиденды. Определить конечную (в пересчете на год) доходность по данной акции (в процентах). Исходные данные: Цена акции по рыночному курсу = 5600 руб. Номинальная стоимость акции = 5000 руб. Фиксированный дивиденд = 7%. Цена продажи= 5700 руб. Решение:Сумма дивидендов за пять лет по привилегированной акции: 5000*0,07*5 = 1750 (руб.) Конечная доходность = ( (1750+ (5700-5600)) / 5600) * (365/1825) * 100% = 6,61%. Пояснения к формуле конечной доходности: а) 5600 (руб) - цена покупки акции б) 5700 (руб) - цена продажи акции в) 1825 - число дней в 5 лет (365*5 = 1825) Задача 4. Инвестор приобрел пакет акций АО в количестве 14 штук номиналом 10 руб. за 2 тыс. руб. Через 1 год и 3 мес. он продал пакет акций за 2,2 тыс. руб. Определить доходность за счет прироста курсовой стоимости (в годовых). Какова была бы доходность операции за счет прироста курсовой стоимости (в годовых), если бы инвестор продал по той же цене акции через 5 месяцев? Решение Доход (от перепрод.)*(срок влад.):(цена приобретения) *100% ((2200-2000)/1,25)/2000*100% = 8% Ответ: Доходность 1 год и 3 мес, за счет прироста составила 8% годовых Доход (от перепрод.)*(срок влад.) :(цена приобретения) *100% ((2200-2000)/1,66)/2000*100% = 16,6% Ответ: Доходность 1 год и 8 мес, за счет прироста составила 16,6% годовых. Задача 5. Инвестор приобрел привилегированную акцию за 20 руб. Дивиденд по акции выплачивается в размере 1 руб. Через 2 года акция была продана за 30 руб. Определите текущую (дивидендную) и конечную доходность Решение:Конечная доходность :dk = ((Ps - Pb)/ n + D)/Pb × 100 %,= ((30-20)/2 + 4)/20*100% = 30% Ps сумма продажи акции-30 Pb сумма покупки акции-20 D диведенты Текущая (дивидендная)доходность: r= (P2 – P1) / P1 * 100=(30-20):20*100=50% P2 цена продажи P1 цена покупки Задача 6. Инвестор «А» купил у инвестора «Б» за 26 руб. привилегированную акцию номиналом 20 руб. Дивиденд по акции выплачивается каждые полгода в размере 10% годовых. Через два года акция была продана за 23 руб. Определить конечную доходность. Сумма дивидендов за пять лет по привилегированной акции: 20*0,1*2 = 4 (руб.) Конечная доходность = = ((Ps - Pb)/ n + D)/Pb × 100 %,= ((26-20)/2 + 4)/20*100% = 35% Задача 7. Инвестор продал акцию за 12 руб. и обеспечил доходность в размере 25% . Какова была бы доходность, если бы инвестор продал акцию по цене на 3 руб. выше? Решение; 1) 12*25%=3руб - доходность 2) 12-3=11руб - номинальная стоимость акции 3) 15-11=4 руб - доходность в рублях 4) 4/15*100%=26,6% доходность Ответ: если бы инвестор продал акцию по цене выше 3 руб, доходность составила бы 26,6%. Задача 8. О чем свидетельствует повышение текущей доходности привилегированной акции, дивиденд по которой носит фиксированный характер? о повышении курсовой стоимости префакции; о понижении курсовой стоимости префакции. Задача 9. Инвестор купил акцию за 2500 рублей и через 100 дней продал ее за 1700 руб. За этот период на акцию был выплачен дивиденд 200 руб. Определите доходность операции инвестора. Решение;r=((Ps-Pb+div)/Pb)*(365/t) = ((1700-100+200)/2500)*( 365/100)*100 = 473% Задача 10. Уставный капитал в 800000 руб. разделен на привилегированные акции (20 % Уставного капитала) и обыкновенные с номинальной стоимостью в 1000 руб. По привилегированным акциям дивиденд установлен в размере 14 % к номинальной стоимости. Какие дивиденды могут быть объявлены по обыкновенным акциям, если на совокупную выплату дивидендов совет директоров рекомендует направить 100 млн. руб. чистой прибыли. Решение 1. Первоначально рассчитываются дивиденды, приходящиеся на привилегированные акции: 1000 х 14% = 140 руб на одну акцию. Номинальная стоимость всех привилегированных акций = 800000 * 0,2 = 160 000 Всего 140 х 160 000 шт. = 22 400 000 руб 2. Затем рассчитывается чистая прибыль, которую можно использовать для выплат по обыкновенным акциям: 100000000- 22 400 000 = 77 600 000 руб 3. Дивиденд, выплачиваемый по одной обыкновенной акции: Номинальная стоимость всех побыкновенной акций = 800 000 * 0,8 = 640 000 77 600 000 : 640 000шт. = 121,25 руб, Доходность облигаций В общем виде доходность является относительным показателем и представляет собой доход, приходящийся на единицу затрат. Совокупный доход определяется как сумма купонного дохода и прироста стоимости облигации. Купонные доход – это произведение купонной ставки, объявленной при эмиссии облигаций, на номинал облигации. Прирост (снижение) стоимости облигации – это курсовая разница между стоимостью покупки и номинальной ценой, выплачиваемой при погашении. Различают текущую доходность и полную (конечную) доходность Текущая доходность. Показатель текущей (купонной) доходности характеризует годовые (текущие) поступления от облигации (купоны) относительно сделанных затрат на ее покупку. 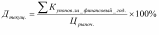 Ц рыноч. – курсовая стоимость облигации, по которой она была приобретена (цена покупки). Ккуп. - сумма выплаченных купонов* -------------------------- * В задачах сумма купонов рассчитывается в % от номинальной стоимости облигаций Текущая доходность облигации является простейшей характеристикой облигации. В текущей доходности не находит отражение еще один источник дохода – изменение стоимости облигации за период владения ею. Показатель полной (конечной) доходности, учитывающий изменение стоимости облигации рассчитывается по формуле: 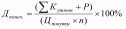 , , где n - период владения* -------------------------- *если период владения активом меньше года, то месяцы (дни) переводим в года: n= 6 мес./12 мес; n= 3 мес./12 мес.; 100 дн./365дн. и т.д. ∑Купонов за весь период – совокупный купонный доход; Р – величина дисконта ( прирост(снижение)) стоимости облигаций. При этом, величина дисконта ( Р )рассчитывается для двух случаев владения облигацией: 1. Если инвестор держит облигацию до погашения, величина дисконта Р равна разнице между номинальной стоимостью облигации (Н) и ценой ее приобретения* --------------------------- * Номинал всех российских облигаций котируемых на бирже составляет 1000 руб. Р= Н - Цпокупки 2. Если инвестор продает облигацию до погашения, то величина Р представляет собой разницу между ценой продажи и приобретения: Р = Цпродажи - Ц покупки. Задача 1. Определить текущую доходность облигации, купленной за 75% к номиналу, если номинальная стоимость облигации составляет 1000 руб., срок обращения 3 года, ежеквартальный купон составляет 5%. Решение; 1. Определим купонные выплаты за год: 1000*5*4/100=200р 2. Далее найдём цену покупки: 1000*75/100=750р 3. Тогда согласно формуле текущей доходности 200/750*100=26,66% Задача 2. Дисконтная облигация со сроком обращения 92 дня была приобретена по цене 95% от номинала. За 25 дней до погашения облигация была продана по цене 99% от номинала. Определить доходность к продаже, если номинальная стоимость облигации составляет 1000 руб. Решение 1. Определим цену покупки и продажи облигаций соответственно: Цпок. = 1000*0,95 = 950 (руб.) Цпрод. = 1000*0,99 = 990 (руб.) 2. Если весь срок обращения облигации 92 дня, а она была продана за 25 дней до погашения, то следовательно, облигация была в обращении: 92 - 25 = 67 (дней) 3.D=((990-950)*365:67):950=22,94% Задача 3. Дисконтная облигация со сроком обращения 92 дня была приобретена по цене 95% от номинала. Определить доходность к погашению, если номинальная стоимость облигации составляет 1000 руб. Решение. 1. Определим цену покупки облигации: =500*0,95=475 2. Из условия задачи нам известны цена погашения и период обращения облигации. Следовательно, доходность дисконтной облигации к погашению будет равна: = (500-475)/475*365/92*100=20,88% Задача 4. Если доходность до погашения по облигации Х равна ее купонной доходности, облигация продается по цене: меньше 100% от номинала; 100% от номинала; больше 100 % от номинала. Задача 5. Определите наиболее выгодный вариант вложения 100 000 руб. на 5 лет: 1) покупка облигаций номиналом 1000 руб. и купоном 8 % годовых; 2) открытие банковского вклада по ставке 4,9% (сложные проценты). Решение 1. Купонный доход за пять лет 110 000 * 0,08 * 5 = 44 000 Дисконтный доход 110 000 – 100 000 = 10 000 Итого доход по облигации 44 000 + 10 000 = 54 000 2.Наращение, сложные проценты (начисление 1 раз в год) 100 000 * (1 + 0,049)5 – 100 000 = 27,20 тыс. руб. Проведя расчет всех двух вариантов вложения, видно, что первый вариант будет наиболее выгодным вложением денег. Задача 6. Облигация с номиналом 1000 рублей и сроком до погашения 1 год куплена на вторичном рынке с дисконтом 2%, а продана через 6 месяцев с премией 3%. Рассчитайте доход инвестора от данной инвестиции, если условиями выпуска облигации предусмотрены купонные выплаты по ставке 20% (выплачиваются 2 раза в год). Решение:Рассчитаем доход от дисконта: 1000*0,05= 50 рублей Рассчитаем доход от премии: 1000*0,03= 30 рублей Рассчитаем купонный доход (так как инвестор владел только пол года облигацией, то получил одну выплату по купону): 1000* 0,2= 200 рублей Рассчитаем совокупный доход: 50+30+200= 280 рублей Ответ: 280 рублей Задача 7. Облигация номиналом 1000 рублей выпушена на срок 3 года. Ежегодно по ней выплачивается процентный доход по ставке 8 %. Облигация приобретена с дисконтом 10 %. Рассчитайте: 1) текущую доходность облигации; Решение 1. Рассчитаем текущий доход облигации по формуле: Dm = (N * r) / 100%, где N – номинальная цена облигации; r – годовая процентная ставка. Dm = (1000*5)/100=50 (руб.) 2. Рассчитав текущий доход, можно рассчитать текущую доходность облигации по формуле: dm = Dm / (B * 100%), где В –цена покупки. Цена покупки в данном случаи составляет 900 руб., т.к. облигация приобретена с дисконтом 10%. dm = 50/(900*100)=5,5 (%) Таким образом, текущая доходность облигации составляет 5,5% |
