рпо. Практикум по сбору и подготовке продукции нефтяных и газовых скважин 2011 Содержание

• Название: Практикум по сбору и подготовке продукции нефтяных и газовых скважин 2011 Содержание
• Дата: 11.04.2022
• Размер: 5.39 Mb.
• Имя файла: Praktikum_po_SPPNGS.doc
• Тип: Практикум; #463047
• страница: 44 из 57

5.ОТСТОЙНИКИ И РЕЗЕРВУАРЫ

5.1.Технологические расчеты отстойников.

Гравитационное разделение фаз.

При сборе и подготовке нефти на промыслах приходится иметь дело с самыми разнообразными смесями, образующими суспензии, эмульсии, пены, туман, дым (пыль). При достаточном различии плотностей дисперсной и дисперсионной фаз наиболее простым методом их разделения является отстаивание.

В поле тяжести на оседающую (всплывающую) частицу действуют: разность силы тяжести и подъемной силы Архимеда

(5.1)
где Δρ - разность плотностей частицы и окружающей среды, g - ускорение свободного падения, d - диаметр частицы, сила сопротивления сплошной среды:

(5.2)
где є_o - коэффициент гидравлического сопротивления сплошной среды движению в ней одиночной частицы, ω_o - скорость движения одиночной частицы, относительно сплошной среды, ρ_с - плотность сплошной среды. Сила конвекционных токов в сплошной среде? Допустим, что температура во всех точках аппарата гравитационного разделения (отстойника) одинакова, тогда конвекционные потоки отсутствуют. При постоянной скорости движения частицы в среде.

ΔF = F_c (5.3)
Откуда, с учетом (5.1) и (5.2),следует

ε_o∙Re_o² = 4 / 3∙Ar (5.4)

где Re_o - критерий Рейнольдса

Re_o = ω_o∙d∙ρ_c∙μ_c, (5.5)

где μ_с – динамическая вязкость сплошной среды, Ar - критерий Архимеда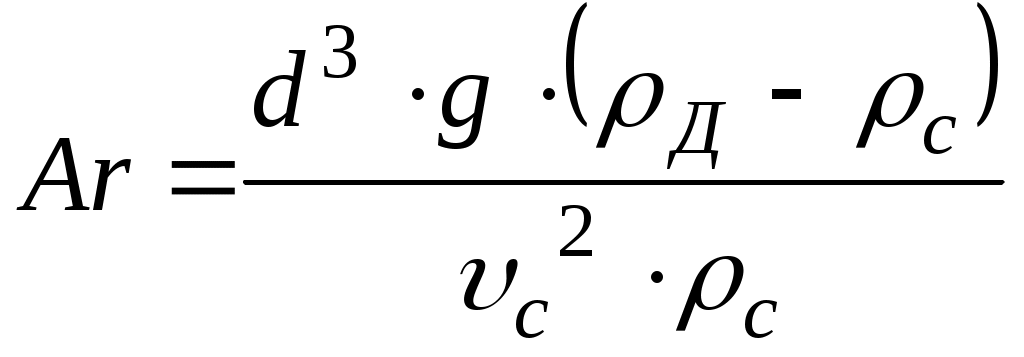

(5.6)
где υ_с - кинематическая вязкость сплошной среды, ρ_д - плотность дисперсной фазы (частицы, капли).

В условиях стесненного осаждения (всплытия) частиц, т. е. при взаимодействии между частицами, имеем аналогично (5.4) равенство
ε_д∙Re_д² = 3 / 4∙Ar (5.7)
где є_д - коэффициент гидравлического сопротивления для дисперсной фазы в эмульсии, Re_д - критерий Рейнольдса в условиях стесненного потока.

Так как правые части (5.4) и (5.7) одинаковы, то
ε_д∙Re_д² = ε_o∙Re_o² (5.8)

Пусть

ε_д = ε_од∙f(α) (5.9)
где є_од - коэффициент гидравлического сопротивления сплошной среды для одной частицы в условиях стесненного потока, α - объемная доля дисперсной фазы в системе,т.е например,обводненность эмульсии. Экспериментальными исследованиями показано, что скорости оседания частицы в условиях свободного осаждения и стесненного потока связаны соотношением
ω_од = ω_о∙(1 - α)ⁿ, (5.10)
где ω_од - скорость осаждения частицы относительно сплошной среды в условиях стесненного потока, ω_о - скорость свободного осаждения частицы.

Поэтому

Re_д = (1 - α)ⁿ∙Re_o (5.11)
Экспериментально также установлено, что при Re < 500



ε_о = С / Re_o ∙ (1 + 0,15 ∙ Re_o ^0,657) (5.12)

где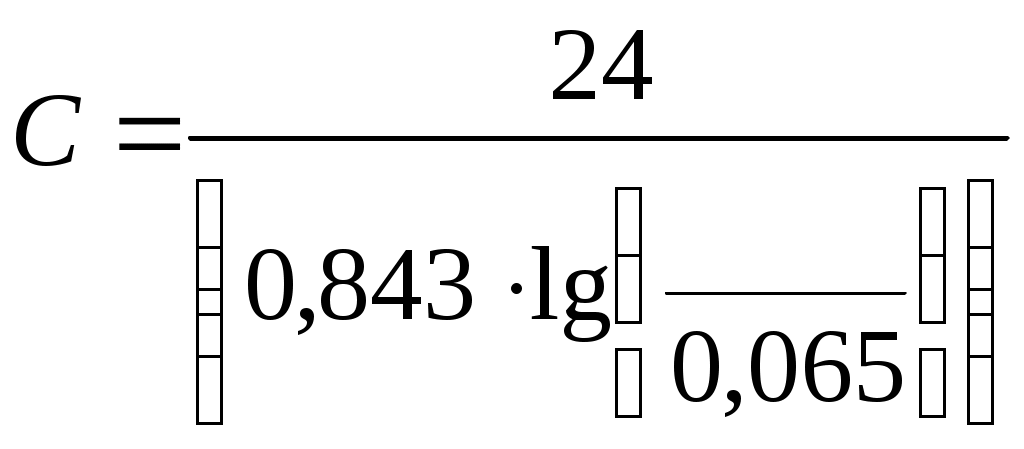



С = 24 / (0,843 ∙ lg(° / 0,065) (5.13)
° - коэффициент формы частицы, равный отношению площадей поверхностей сферической частицы и реальной частицы одинакового объема. Для сферических частиц ° = 1, следовательно С = 24.

Из (5.8) и (5.9) следует:
ε_о∙Re_o² = ε_од∙f(α)∙Re_д² (5.14)
Откуда, с учетом (5.12), получают
Re_o∙(1 + 0,15∙Re_o^0,687) = f(α)∙Re_д∙(1 + 0,15∙Re_д^0,687) (5.15)
При малых Re из (5.11) и (5.15) следует
f(α) = (1 - α)ⁿ (5.16)
При Re > 500 коэффициент сопротивления не зависит от скорости, следовательно, є_о = є_од, поэтому из (5.14)
Re_o² = f(α)∙Re_д² (5.17)
Тогда из (5.11) и (5.17) имеем:
f(α) = (1 - α)^(-2n) (5.18)
Экспериментальными исследованиями установлено, что f(α), определяемая по (5.16) и (5.18), изменяется от (1 - α)^(-4,65) до (1 - α)^(-4,78), следовательно, в первом приближении принимают, что

f(α) = (1 - α)^(-4,7) (5.19)
Поэтому вместо (5.10) можно записать:
ω_од / ω_о = (1 - α)^4,7 (5.20)
Известны также следующие эмпирические формулы для учета влияния стесненности:

при α<0,3

ω_од / ω_о = (1 - α)²∙10^(-1,82∙α) (5.21)

при α≥0,3

ω_од / ω_о = 0,123 / α∙(1 - α)³ (5.22)
Расчет скорости осаждения капель при известном их диаметре.
Область ламинарного режима осаждения характеризуется следующими значениями параметра Рейнольдса:

10^(-4) < Re ≤ 2 (5.23)
Соответственно коэффициент гидравлического сопротивления среды движению капли при этом режиме равен:
ε_о = 24 / Re (5.24)
Из (5.4) с учетом (5.24) следует
Re = Ar / 18 (5.25)
Используя граничные значения критерия Рейнольдса, из (5.23) по (5.25) легко рассчитать граничные значения критерия Архимеда в области ламинарного режима осаждения капель:
18∙10^(-6) < Ar ≤ 36 (5.26)
В области переходного режима осаждения:
2 < Re ≤ 500, (5.27)
а коэффициент гидравлического сопротивления среды осаждению капли определяют по формуле Аллена

ε_о = 18,5 / Re^0,6 (5.28)
Из (5.4) с учетом (5.28) для критерия Рейнольдса получается
Re = Ar^{0,714 / 6,545} (5.29)
По аналогии с выводом (5.26) из (5.29) с учетом граничных значений критерия Re (5.27) следует, что соответствующие граничные значения критерия Архимеда в области переходного режима осаждения капель будут
36 < Ar ≤ 83,3∙1000 (5.30)
Так как критерий Рейнольдса:
Re = ω_o∙d∙ρ_c / μ (5.31)
То при известном диаметре частицы и значении Re (5.31) следует:

(5.32)

Таким образом, в области ламинарного режима скорость осаждения частицы равна:

(5.33)

в области переходного режима осаждения:

(5.34)

Итак для расчета скорости свободного осаждения капель при известном их диаметре, вначале рассчитывают критерий Архимеда:
Ar = d³∙ρ_c∙(ρ_д - ρ_с) / μ² (5.35)
а, если его значение удовлетворяет неравенствам (5.26), то скорость считают по (5.32), а если - соответственно неравенствам (5.30), то по (5.34).
Расчет отстойной аппаратуры
Технологический расчет отстойной аппаратуры заключается в определении пропускной способности отстойника или его размеров.

Если скорость слияния капель воды с водной подушкой - слоем воды в отстойнике меньше скорости накопления частиц на водонефтяном разделе, то между нефтью и водной подушкой образуется переходной слой, толщина которого уменьшается к выходу от отстойника.

Обводненность нефти на выходе из отстойника определяют по содержанию мелких капель воды, время осаждения которых больше времени осевого перемещения разделяемой эмульсии в отстойнике. Скорость движения эмульсии вдоль отстойника от входа до выхода непрерывно уменьшается от значения на входе:
ω_вх = Q_ж / S_н (5.36)

до значения на выходе:

ω_вых = Q'_н / S_н (5.37)
где Q_ж - количество жидкости (эмульсии), непрерывно поступающее в отстойник для разделения за единицу времени, S_н - площадь поперечного сечения, занятая слоем нефти (эмульсии) на входе в отстойник, Q'_н - количество эмульсии с остаточным содержанием воды, непрерывно вытекающее из отстойника в единицу времени.

За время прохождения эмульсии от входа до выхода из отстойника концентрация дисперсной фазы в эмульсии изменяется. В верхней части отстойника она уменьшается по сравнению с первоначальной концентрацией. Следовательно, вязкость эмульсии по высоте в отстойнике переменна, причем в верхней части отстойника она уменьшается вдоль горизонтальной оси от входа до выхода. По вертикали в каждом сечении отстойника вязкость эмульсии возрастает от минимальной у верхней образующей отстойника до максимальной на границе с водной подушкой. Такой сложный характер изменения вязкости эмульсии в отстойнике определяется кинетикой гравитационного разделения фаз. Следовательно, горизонтальная составляющая скорости эмульсии в отстойнике максимальна в верхнем и минимальна в нижнем слоях эмульсии.

Принимая время осаждения максимальных капель воды, выносящихся потоком нефти, равным времени движения эмульсии вдоль зоны отстоя, получаем возможность рассчитать пропускную способность отстойника:

(5.38)

где R - радиус отстойника, h - высота слоя воды в отстойнике, ω_одi – скорость осаждения капель воды диаметром d_i в эмульсии, из которой выносятся потоком нефти все отставшие капли меньшего размера, l - часть длины отстойника от сечения, где начинается гравитационное разделение эмульсии (воды), до сечения, где оно прекращается (выход).

Из (5.38) следует:

(5.39)
Пропускная способность отстойника из (5.36) определяется как
Q_ж = ω_вх∙S_н (5.40)
Так как средняя скорость движения эмульсии в отстойнике может быть принята как средняя арифметическая на входе и выходе, то
ω_ср = 0,5∙(ω_вх + ω_вых) (5.41)

Откуда:

ω_вх = 2∙ω_ср - ω_вых (5.42)

или с учетом (5.37):

ω_вх = 2∙ω_ср - Q'_н / S_н (5.43)
Таким образом, пропускная способность отстойника будет:
Q_ж = 2∙ω_ср∙S_н - Q'_н (5.44)
Из материального баланса работы отстойника, пренебрегая захватом нефти дренажной водой, можно показать, что:

(5.45)

Следовательно, из (5.44) с учетом (5.45) после преобразований имеем: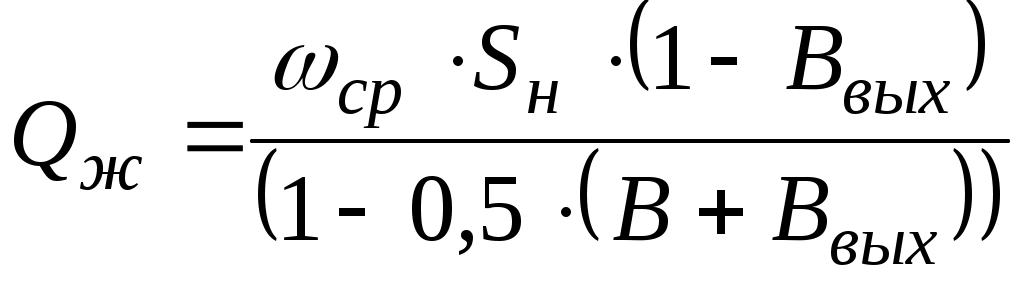

(5.46)

Подставляя (5.39) в (5.46),получим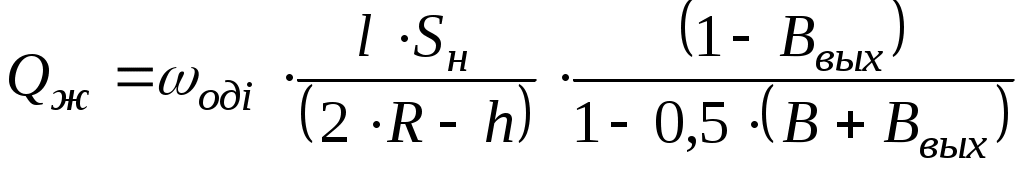

(5.47)

Так как скорость стесненного осаждения капель равна: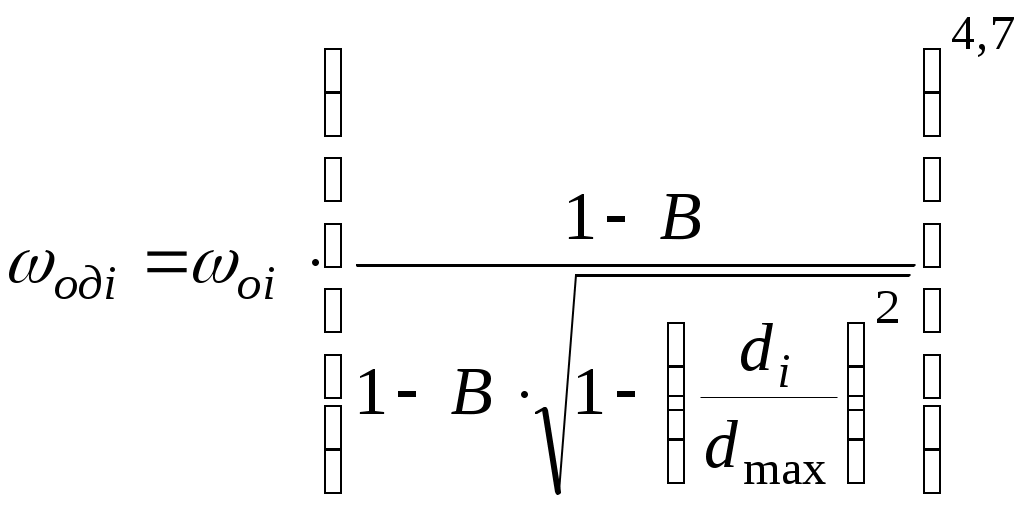

, (5.48)
а свободного при Re < 2 – соответственно:

, (5.49)
то пропускная способность отстойника будет:

, (5.50)

где F(В, В_вых) - функция обводненности на входе и выходе из отстойника.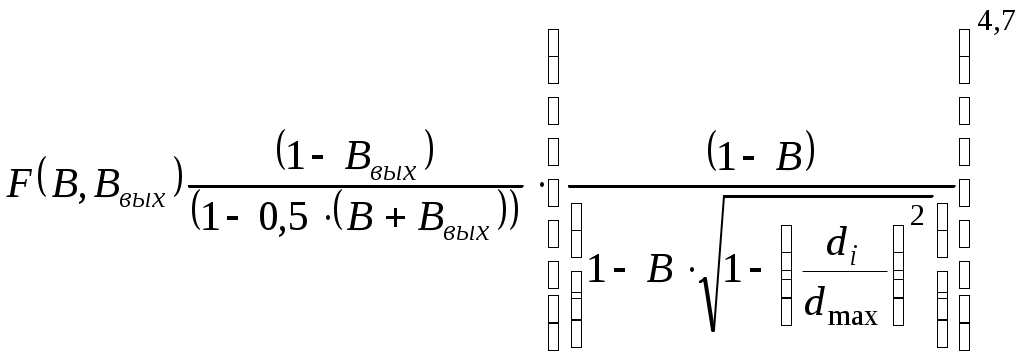

(5.51)

где ρ_в, ρ_н - плотность воды и эмульсии в отстойнике соответственно, кг/м³, l - длина зоны отстоя, м, S_н - площадь поперечного сечения отстойника, занятая эмульсией на входе в зону отстоя, м, R - радиус отстойника, м, h - максимальная высота водной подушки в отстойнике в зоне отстоя, м, μ_н - вязкость нефти в отстойнике, Па∙с, di - максимальный диаметр капель воды, которые вместе с каплями меньшего размера могут выносится из отстойника потоком нефти, м, В, В_вых - обводненность эмульсии на входе в зону отстоя и выходе из нее, d_мах -

максимальный размер капель воды в эмульсии на входе в зону отстоя, м.

Из предыдущего следует, что: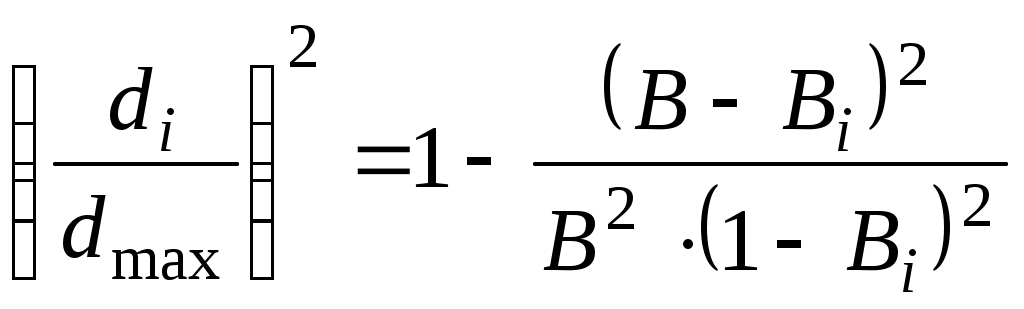



(5.52)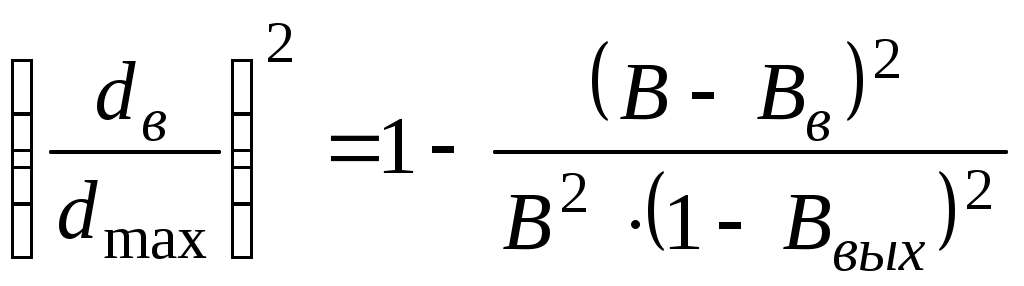



где d_в - максимальный диаметр капель, выносимый из отстойника с потоком нефти.

Связь между d_i и максимальным диаметром капли, выносимым из отстойника можно установить следующим образом.

Перед выходом нефти из отстойника в зоне отстоя в дренаж уходит последняя капля d_i, которая являлась для остающихся капель максимальной, поэтому обводненность слоя эмульсии с каплями d_в может быть, по аналогии с (5.52),представлена в виде: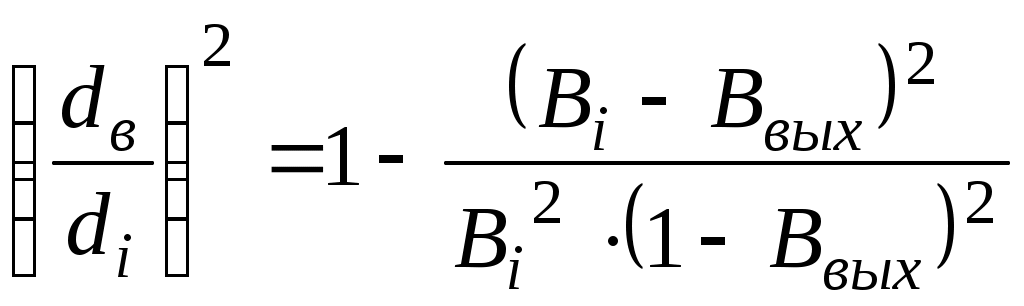

(5.53)

Таким образом, система уравнений (5.52) и (5.53) содержит три неизвестных d_i, d_в, и В_i, следовательно, может быть решена. Представим (5.50) в виде: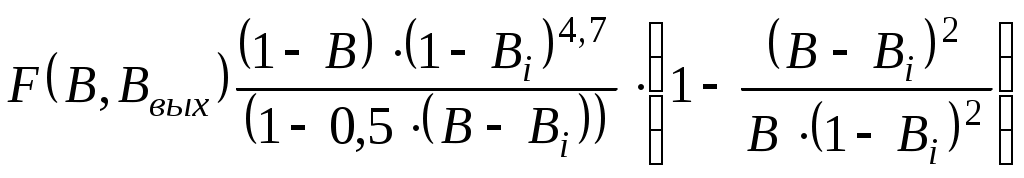

(5.54)

где

(5.55)

Необходимо отметить, что доля воды в потоке нефти на выходе их отстойника является функцией высоты водяной подушки, пропускной способности отстойника и его конструктивных параметров. Как правило, в дренажной воде содержится примесь нефти, количество которой также является функцией перечисленных параметров. Поэтому расчет пропускной способности отстойника приближенный.

Типовые задачи

Типовая задача 5.1

Сопоставить расчетные относительные скорости оседания капель воды в нефти в зависимости от ее обводненности, определенной по (5.20), (5.21) и (5.22)

Решение:

Пусть обводненность водонефтяной эмульсии равна 5%, тогда по (5.20)
ω_од / ω_о = (1 – 0,05)^4,7 = 0,7858

по (5.21)

ω_од / ω_о = (1- 0,05)² ∙10^{(-1,82 ∙0,05)} = 0,7319
Разность результатов расчетов составляет:
0,7858 – 0,7319 = 0.0539
Результаты аналогичных расчетов для других обводненностей представлены в таблице. Как следует из таблицы, сравниваемые формулы дают близкие результаты, поэтому пользоваться можно любыми из них. Надо вычислять в %, тогда можно сравнивать.
Таблица: 5.1

Сопоставление результатов расчетов

Обводненность в %	Результаты расчетов по формулам			Разность
	6,2	6,21	6,22
5	0,7858	0,7319	-	0,0539
10	0,6095	0,5327	-	0,0768
20	0,3504	0,2768	-	0,0736
30	0,1871	-	0,1406	0,0465
40	0,0906	-	0,0664	0,0242
50	0,0385	-	0,0308	0,0077
60	0,0135	-	0,0131	0,0004

Типовая задача 5.2

Рассчитать скорости свободного осаждения капель воды 12 размеров в нефти, если вязкость нефти μ_н = 3 мП∙с, плотность ρ_н = 820 кг/м³. Размеры капель воды (плотностью ρ_в = 1100 кг/м³) следующие:3, 4, 5, 10, 20, 30, 40, 50, 60, 80, 100, 200 мкм.

Решение:

Пусть капля воды диаметром 20 мкм. По (5.35) определяют критерий Архимеда
Ar = (20∙10^(-6))³∙820∙(1100 - 820)∙9,81 / (3∙10^(-3))² = 20,021∙10^(-4)
Так как 18∙10^(-4) < 20,021∙10^(-4) < 36, то по (5.33) рассчитывают скорость свободного осаждения капель воды диаметром 20мкм в нефти:
ω_о = 20,021∙10^(-4)∙3∙10^(-3) / (18∙820∙20∙10^(-6)) = 2,03∙10^(-5) м/с = 7,3 см/ч
Результаты аналогичных расчетов для других размеров капель представлены в таблице 5.2.
Таблица: 5.2

Результаты расчетов

Диаметр капель воды, мкм	КритерийАрхимеда	Скорость своб-го осаждения, см/ч	Примечания
3	0,068∙10(-4)	-	Частицы с такими размерами, что скоростями осаждения можно пренебречь.   Область ламинарного Режима осаждения.
4	0,160∙10(-4)	-
5	0,3313∙10(-4)	-
10	2,503∙10(-4)	1,8
20	20,021∙10(-4)	7,3
30	67,571∙10(-4)	16,4
40	1,6017∙10(-2)	29,5
50	3,1283∙10(-2)	45,9
60	5,4057∙10(-2)	65,9
80	12,8135∙10(-2)	117,2
100	0,2503	183,1
200	2,0021	732,5

Типовая задача 5.3

Рассчитать скорости стесненного осаждения капель воды по условиям предыдущей задачи, для следующей обводненности эмульсий: 5, 10, 20, 30, 40, 50, 60, 70%.

Решение:

Исследованиями установлено, что при объемном содержании дисперсной фазы более 5% необходимо учитывать стесненность осаждения (всплытия капель).

По (5.20) для условий предыдущих типовых задач получим
ω_од = ω_о∙(1 - В)^4,7
Значение ω_о берут из решения задачи 5.2, а комплекса (1 - В) из задачи 5.1.

Например, пусть диаметр капли воды равен 50мкм, скорость ее свободного осаждения равна 45,9 см/ч, а параметр (1 - В)^4,7 равен при 50%-ной обводненности 0,0385, следовательно
ω_од = 45,9∙0,0385 = 1,77 см/ч
т.е. скорость стесненного осаждения при 50%-ной обводненности эмульсии в 26 раз меньше скорости свободного осаждения капель. Результаты в таблице 5.3
Таблица: 5.3

Результаты расчетов

Диаметр капель, мкм	Скорость осаждения (см/ч) при различной обводненности, %
	5	10	20	30	40	50	60	70
10	1,41	1,1	0,63	0,34	0,16	0,07	0,02	0,009
20	5,74	4,45	2,56	1,37	0,66	0,28	0,1	0,03
30	12,89	10	5,75	3,07	1,49	0,63	0,22	0,06
40	23,18	18,01	10,34	5,52	2,67	1,13	0,4	0,1
50	36,07	27,97	16,08	8,59	4,16	1,77	0,62	0,16
60	51,78	40,16	23,09	12,33	5,97	2,54	0,89	0,23
80	92,09	71,43	41,06	21,92	10,62	4,51	1,58	0,44
100	143,88	111,59	64,15	34,25	16,6	7,04	2,47	0,61
200	575,59	446,43	256,64	137,01	66,39	28,18	9,87	2,53

Типовая задача 5.4

Рассчитать необходимую длину зоны отстоя при непрерывной подаче эмульсии в отстойник, если ее обводненность B = 0,2, распределение частиц по размерам представлено, высота слоя эмульсии на входе 1,75 м, горизонтальная составляющая скорости эмульсии на входе ω_г = 10 м/ч, вязкость нефти 3 мПа∙с, плотность воды 1100 кг/м³.

Решение

Необходимую длину зоны отстоя эмульсии определяют остаточной водонасыщеностью, горизонтальной составляющей скорости движения эмульсии и скоростью расслоения эмульсии.

Из-за перехода части воды из эмульсии в водную фазу через водонефтяной контакт горизонтальная скорость перемещения эмульсии непрерывно уменьшается, поэтому
l≤ ω_г∙t, (5.56)
где l - длина зоны отстоя эмульсии, м; ω_г - горизонтальная скорость движения эмульсии на входе в отстойник, м/с; t - время пребывания эмульсии в отстойнике, с.
Время пребывания эмульсии в отстойнике может быть определено как отношение
t_i = h / ω_одi, (5.57)
где h - высота слоя водонефтяной эмульсии на входе в отстойник, ω_одi - скорость стесненного оседания капель воды диаметром d_i; t_i - время оседания частиц диаметром di, т. е. время прохождения их через слой эмульсии высотой h.

Подставляя (5.57) в (5.56) получаем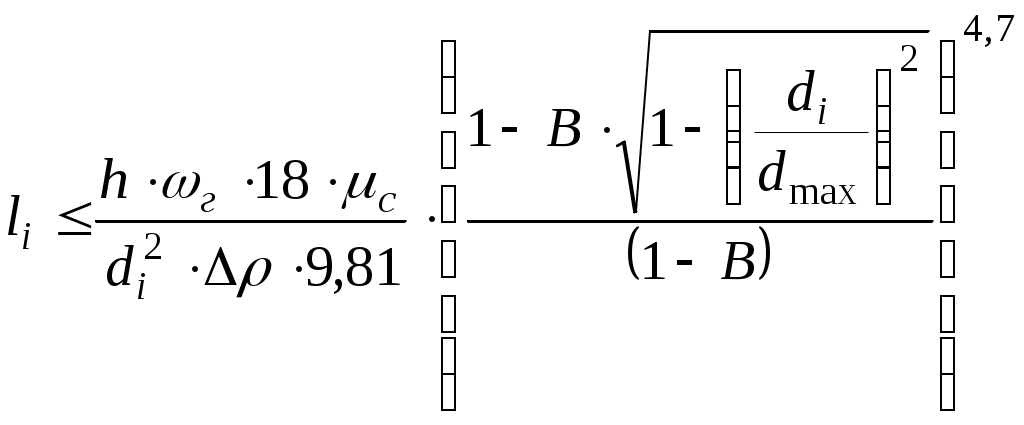

,

где μ_с - вязкость среды; d_i - максимальный диаметр капель воды, которые могут содержаться в эмульсии на выходе из отстойника, м;
Δρ = ρ_в - ρ_н, (5.58)
ρ_в, ρ_н - плотности воды и нефти соответственно, кг/м³; d_max - максимальный

диаметр капель воды в эмульсии на входе в отстойник, м; l_i - длина зоны отстоя капель воды диаметром более d_i, м.

Пусть d_i = 100 мкм, тогда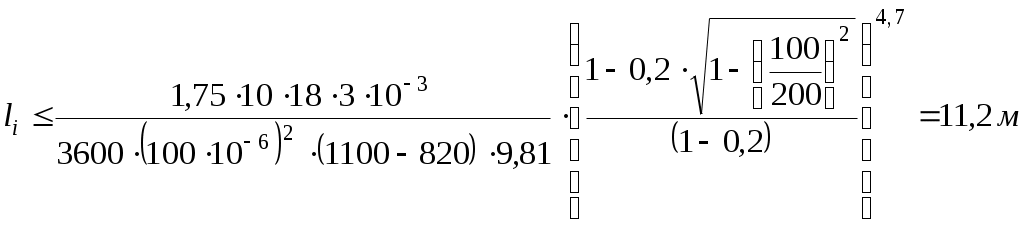



Если зона отстоя эмульсии 11,2 м, то осаждаются все капли воды в эмульсии диаметром 100 мкм и более. Следовательно, в эмульсии на выходе могут содержаться только капли воды диаметром меньше 100мкм. В соответствии с заданным распределением капель воды в эмульсии по размерам на выходе из отстойника с длиной зоны отстоя 11,2 м содержаться капли размером 100мкм и меньше.

Обводненность эмульсии на выходе из отстойника может быть рассчитана, принимая размеры капель воды, покидающих отстойник в составе эмульсии, 80 мкм и меньше: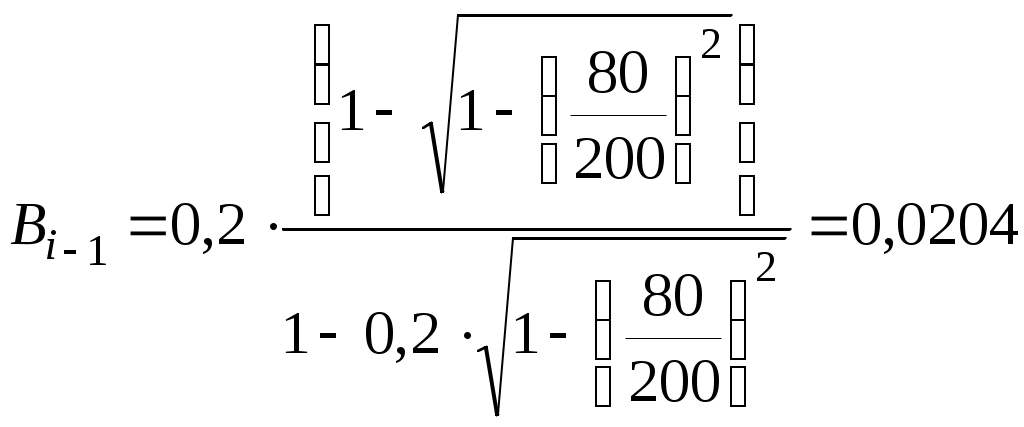



Для d_i = 200; l_i = 6,8, B_i = 2,04%
Таким образом, при длине зоны отстоя не более 7 м обводненность эмульсии на выходе из отстойника составляет 2,04 %. Дальнейшее увеличение длины зоны отстоя и, как следствие, длины отстойника не существенно снижает содержание остаточной воды в эмульсии.
Типовая задача 5.5
Рассчитать диаметр и длину отстойной секции гравитационного булита-отстойника, обеспечивающего заданную пропускную способность и степень разделения эмульсии на нефть и воду.

Решение:

Эффективное разделение фаз в гравитационном отстойнике происходит при условии соблюдения в зоне отстоя ламинарного режима течения эмульсии, т.е. при Re ≤ 2300. Следовательно,
Re = v_ж∙D_э∙ρ_ж / μ_ж ≤ 2300, (5.59)
где v_ж - скорость горизонтального движения эмульсии в зоне отстоя в отстойнике, м/с; D_э - эквивалентный гидравлический диаметр поперечного сечения потока эмульсии в отстойнике на входе в зону отстоя, м; ρ_ж, μ_ж - плотность и вязкость эмульсии на входе в зону отстоя, кг/м³ и Па∙с, соответственно.

Скорость потока эмульсии на входе в зону отстоя
v_ж = Q_ж / S_н = 4Q_ж /(π∙D_э²), (5.60)
подставляя (5.60) в (5.59) получим

(5.61)

Известно, что

D_э = D∙((1 /π)∙f(е))^0,5, (5.62)

Где

, (5.63)

Поэтому диаметр булита-отстойника с водяной подушкой на заданную пропускную способность может быть рассчитан по формуле
, (5.64)
где Q_ж - нагрузка на , высоты водяной подушки в зоне отстоя.

При е = 0,46 пропускная способность гравитационного отстойника максимальна.

Учитывая, что f(0,246) = 2,596 и подставляя в (5.64), получают

(5.65)

Из (5.65) следует, что ПРОПУСКНАЯ СПОСОБНОСТЬ гравитационного отстойника заданного диаметра высотой водяной подушки 0,23D может быть рассчитана по той же формуле, т. е.
Q_ж≤1645∙D∙μ_ж / ρ_ж, (5.66)
Необходимую ДЛИНУ отстойника определяют из условия равенства времени осаждения капель воды от верхней образующей до водонефтяного раздела и времени их пребывания в зоне отстоя

(D - h) / ω_одi = l / v_ж, (5.67)
где ω_одi - скорость стесненного осаждения капли воды диаметром d_i в полидисперсной эмульсии в зоне отстоя, м/с; l - эффективная длина зоны гравитационного разделения отстойника, т.е. длина зоны отстоя, не возмущаемая условиями ввода и вывода эмульсии, м; v_ж - горизонтальная скорость движения эмульсии в зоне отстоя, м/с; h - высота слоя водяной подушки, м.

Так как

ω_одi = ω_оi(1 - B_i)^4,7, (5.68)
то из (5.67) после преобразований и подстановки (5.64) следует

(5.69)
При е = 0,46 получают

(5.70)
Типовая задача 5.6

Диаметр отстойника 3,4 м, плотность нефти 860 кг/м³, воды 1100 кг/м обводненность эмульсии на входе 30%, вязкость нефти 5 мПа∙с. Оценить пропускную способность отстойника по жидкости по (5.66).

Решение

Плотность эмульсии рассчитывают по правилу аддитивности:
ρ_ж = ρ_н∙(1 - В) + ρ_в∙В = 860∙(1 – 0,3) + 1100∙0,3 = 932 кг/м³
Вязкость эмульсии оценивают по формуле:

=

Тогда пропускная способность булита-отстойника типа УПС-6300/6М обеспечивающего ламинарный режим движения, при принятых параметрах будет
Q_ж = 1645∙3,4∙12∙10^-3∙86400 / 932 = 6220 м³/сут
Типовая задача 5.7

Определить необходимый диаметр горизонтального отстойника для предварительного сброса воды с относительной высотой водяной подушки в нем е = 0,46, если максимальная нагрузка на него по жидкости не превысит 6300т/сут, а обводненность эмульсии в зоне отстоя колеблется от 30 до 45%. Вязкость нефти в условиях эксплуатации отстойника из-за температурных колебаний может изменяться от 3,5 до 4 мПа∙с.

Решение:

Как следует из формулы (5.65), справедливой для е=0,46, диаметр отстойника, в котором будет обеспечен ламинарный режим движения эмульсии в зоне отстоя, прямо пропорционален нагрузке на него и обратно пропорционален вязкости эмульсии.

Допускают, что вязкость эмульсии может быть оценена по формуле
μ_ж = μ_н / (1 - В)^2,5,
где В - обводненность эмульсии; μ_ж, μ_н - вязкость эмульсии и нефти соответственно, тогда



При прочих равных условиях максимальный диаметр отстойника получается при минимальном значении обводненности эмульсии. Поэтому принимают в расчетах

В = 0,3, вязкость нефти μ_н = 3,5мПа∙с и получают, что



При прочих равных условиях диаметр отстойника минимален при максимальной

обводненности эмульсии. Поэтому принимают в расчетах В = 0,45, вязкость нефти μ_н = 4мПа∙с и получают, что



Отстойники диаметром более 3,4м промышленностью не выпускаются, следовательно, выбирают отстойник диаметром 3,4м. Но выбранный отстойник не может обеспечить необходимую нагрузку на него в 6300т/сут при ламинарном режиме течения эмульсии в нем и при других значениях входных параметров. Поэтому оценивают допустимую нагрузку на него при обводненности В = 0,3 и вязкости нефти μ_н =3,5 мПа∙с по (5.66) имеем

= или

Таким образом, при нагрузке 6300 т/сут необходимо установить не менее двух отстойников диаметром 3,4 м.

Допустимую нагрузку на отстойник в наиболее тяжелых условиях, если диаметр отстойника 2м, оценивают по (5.66)


Нагрузку 6300 т/сут можно пропустить только через три отстойника диаметром 2 м.

Наиболее выгодный вариант может определить только технико-экономический анализ.

Задания для домашней и самостоятельной работы

Задача 5.1.

Как будет влиять температура на скорость процесса разделения нефти и воды методом отстаивания в резервуарах?

Рекомендации. Сравните влияние температуры на изменение плотностей минерализованной воды и нефти и на разность плотностей нефти и воды. Результат представьте графически.

Диапазон изменения температуры и характеристику воды принять по условиям задачи 1.20 («Физико-химические свойства пластовых и сточных вод»). Для расчета плотности нефти при заданных температурах воспользуйтесь формулой из раздела 1.4 для вычисления величины коэффициента термического расширения в зависимости от плотности нефти.

Результат представьте графически.ρ_в=f(T), ρ_н=f(T), (ρ_в- ρ_н)=f(T).

Таблица 5.4