Урок 3.26
Изучим граф

a, b, c, d, e, f, g, h = range(8)
N = [
{b:2, c:1, d:3, e:9, f:4}, # a
{c:4, e:3}, # b
{d:8}, # c
{e:7}, # d
{f:5}, # e
{c:2, g:2, h:2}, # f
{f:1, h:6}, # g
{f:9, g:8} # h
]
print (N)
if b in N[a]: # смежная?
print ('yes')
print(len(N[f])) # степень
print(N[a][b]) # вес (a, b)
Задание
Создайте модель графа на питоне.
Выясните программно: 1)вес ребра 2-3, 2)степень вершины 4, 3)смежность вершин 3 и 9

|
Урок 3.27
Если в графе любые две вершины соединены путем, то такой граф называется связным.
Дан граф, в котором выделена вершина s. Требуется найти все вершины, лежащие в одной компоненте связности с ней. Иными словами, нужно понять, до каких вершин можно добраться из s
#
# 2--0--6--7 1--9 5
# | | |
# 3--4 8
#
n = 10
adj_list = [[2, 4, 6],
[9],
[0, 3],
[2, 4],
[0, 3],
[],
[0, 7, 8],
[6],
[6],
[1]]
s = 0
visited = [False] * n # массив "посещена ли вершина?"
def dfs(v):
visited[v] = True
for w in adj_list[v]:
if visited[w] == False: # посещён ли текущий сосед?
dfs(w)
dfs(s)
print(visited.count(True))
Задание
  
7
6
Найдите все компоненты связности вершины 1

|
Урок 3.28 Проверка связности двух вершин
#
# 2--0--6--7 1--9 5
# | | |
# 3--4 8
#
n = 10
adj_list = [[2, 4, 6],
[9],
[0, 3],
[2, 4],
[0, 3],
[],
[0, 7, 8],
[6],
[6],
[1]]
visited = [False] * n
component = [-1] * n # для каждой вершины храним номер её компоненты
num_components = 0
def dfs(v):
component[v] = num_components
visited[v] = True
for w in adj_list[v]:
if visited[w] == False:
dfs(w)
visited = [False] * n
for v in range(n):
if not visited[v]:
dfs(v)
num_components += 1
print(component[6] == component[8])
Задание проверьте связность вершин 1 и 4, 1 и 6
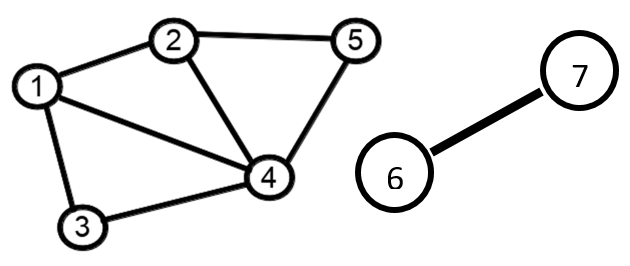
|
Урок 3.29 Количество путей
Н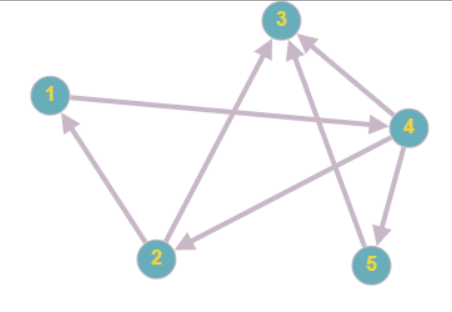
айдем количество путей в графе от вершины до вершины 3
Graph = [ [ ], # фиктивный элемент
[4], # список смежности # для вершины 1
[1,3], # для вершины 2
[ ], # для вершины 3
[2,3,5], # для вершины 4
[3] ] # для вершины 5
def pathCount ( graph, vStart,vEnd, visited ):
if vStart == vEnd:
return 1
visited.append ( vStart )
count = 0
for v in graph[vStart]:
if not v in visited:
count += pathCount ( graph, v, vEnd,visited)
visited.pop()
return count
print ( pathCount (Graph, 1, 3, [ ]) )
Задание
Найдите количество путей в графе от А до Ж (см. далее)
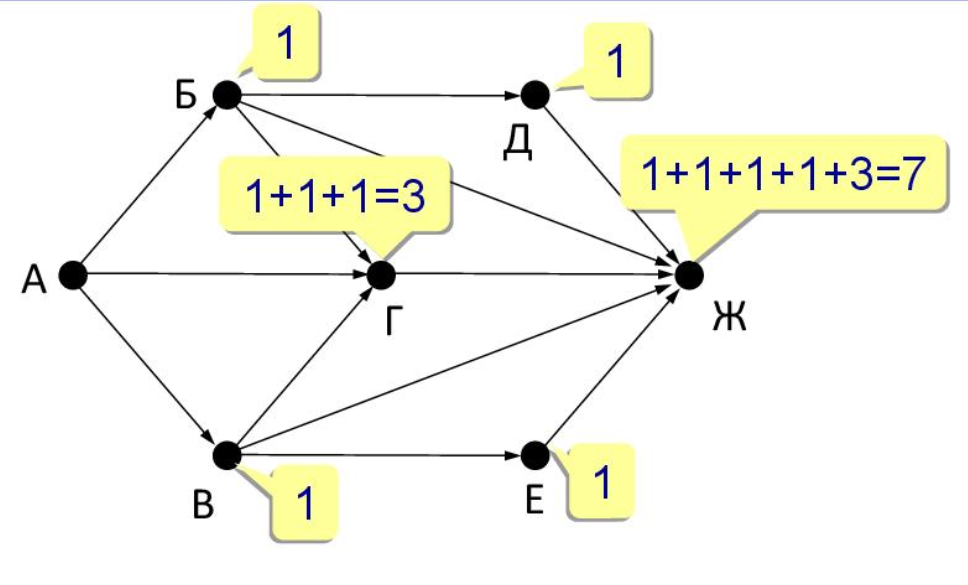
|
Урок 3.30 Обход вершин графа
Алгоритм поиска (или обхода) в глубину (англ. depth-first search, DFS) позволяет построить обход ориентированного или неориентированного графа, при котором посещаются все вершины, доступные из начальной вершины.
Поиск в глубину
# Смежность вершин
inc = {
1: [2, 8],
2: [1, 3, 8],
3: [2, 4, 8],
4: [3, 7, 9],
5: [6, 7],
6: [5],
7: [4, 5, 8],
8: [1, 2, 3, 7],
9: [4],
}
visited = set() # Посещена ли вершина?
# Поисквглубину - ПВГ (Depth First Search - DFS)
def dfs(v):
if v in visited: # Если вершина уже посещена, выходим
return
visited.add(v) # Посетили вершину v
for i in inc[v]: # Все смежные с v вершины
if not i in visited:
dfs(i)
start = 1
dfs(start) # start - начальнаявершинаобхода
print(visited)
Поиск в ширину
# Смежность вершин
inc = {
1: [2, 8],
2: [1, 3, 8],
3: [2, 4, 8],
4: [3, 7, 9],
5: [6, 7],
6: [5],
7: [4, 5, 8],
8: [1, 2, 3, 7],
9: [4],
}
visited = set() # Посещена ли вершина?
Q = [] # Очередь
BFS = []
# Поиск в ширину - ПВШ (Breadth First Search - BFS)
def bfs(v):
if v in visited: # Если вершина уже посещена, выходим
return
visited.add(v) # Посетили вершину v
BFS.append(v) # Запоминаем порядок обхода
# print("v = %d" % v)
for i in inc[v]: # Всесмежныес v вершины
if not i in visited:
Q.append(i)
while Q:
bfs(Q.pop(0))
start = 1
bfs(start) # start - начальнаявершинаобхода
print(BFS) # Выводится: [1, 2, 8, 3, 7, 4, 5, 9, 6]
Напишите программу для обхода вершин графа

|
Урок 3.31
Алгоритм Дейкстры. Кратчайший путь
Дан ориентированный взвешенный граф.
Найдите кратчайший путь от одной заданной вершины до другой.
n,start,end =3,2,1 #n-число вершин,start-стартовая вершина,end-конечная вершина
d=[] #минимальные расстояния
v=[] #посещенные вершины
print(n,start,end)
a=[[0,4,2],[4,0,1],[2,1,0]]
#вывод матрицы
for i in range(len(a)):
for j in range(len(a[i])):
print(a[i][j], end=' ')
print()
# инициалиация вершин
for i in range(n):
d.append(1000) # все вершины имеют максимально большое значение
v.append(False) # пометить вершины как не обработанные
start-=1# -1 та как, в массивах нумерация идёт с нуля
end-=1
d[start]=0 # значение стартовой вершины
v[start] = True # стартовая вершина отработана
#шаг1
for j in range(n):
for i in range(n):
if i==start:
continue
if v[i] == False and a[start][i]< d[i] and a[start][i]!=0:
d[i]=d[start]+a[start][i]
start= 0
print(d)
Задание
Проверьте работу программы на компьютере для матрицы 4х4 с произвольными данными.
| Дополнительный материал
Задачи
1 Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера, Земля — Плутон, Плутон - Меркурий, Меркурий - Венера, Уран - Нептун, Нептун - Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. Можно ли добраться (возможны пересадки) с Земли до Марса?
2 Сколькими способами, двигаясь по указанным отрезкам, можно кратчайшим путем переместиться из точки А в точку В?
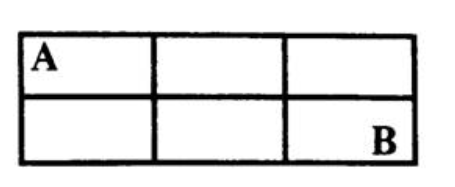
|
Гамильтонов цикл
гамильтоновым циклом является такой цикл (замкнутый путь), который проходит через каждую вершину данного графа ровно по одному разу
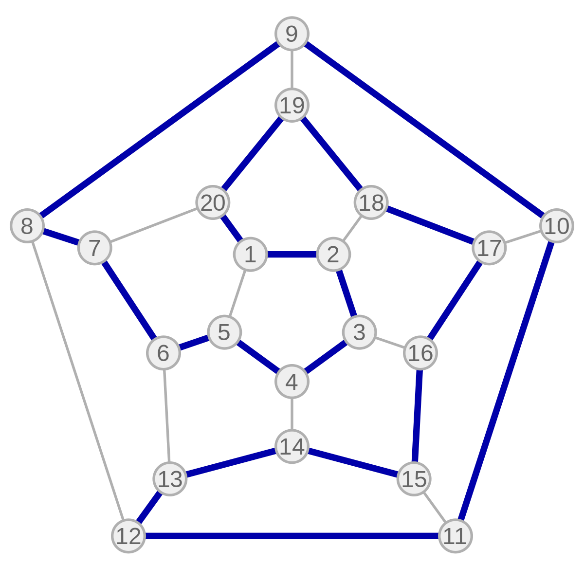
def hamiltomian_circuit(start, vertices, graph):
result = [start]
while result:
if graph[result[-1]]:
vertex = graph[result[-1]].pop()
if vertex not in result:
result.append(vertex)
else:
del graph[result[-1]]
result.pop()
if len(result) == vertices:
break
return result
vertices = 5
edges = ['0 4', '0 1', '1 2', '2 1',
'2 3', '3 2', '3 4', '4 3',
'0 3', '3 0', '0 2', '4 1']
origin_graph = {}
for edge in edges:
source, destination = edge.split()
if source not in origin_graph:
origin_graph[source] = []
origin_graph[source].append(destination)
path = []
for source in origin_graph:
path = hamiltomian_circuit(source, vertices, origin_graph.copy())
if path:
break
print(' '.join(path)) # 0 2 3 4
|
Задачи на принадлежность точки к области, ограниченной линиями.
Введите с клавиатуры координаты точки А(x, y). Определите, попадает ли точка А в область, ограниченной линиями y=x, y=-x и y=1, не включая границы.
Входные данные: два числа x, y.
Выходные данные: слово «Да», если точка попадает в заштрихованную область, не включая ее границы и слово «Нет» в противном случае.
x,y = map(int, input().split())
p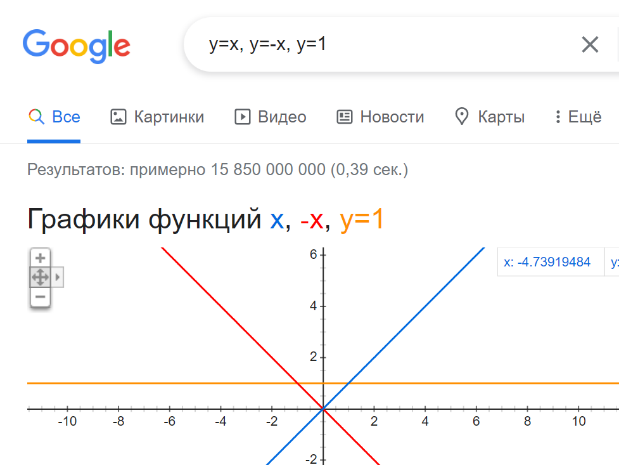 rint("y" if abs(x)<1 and 1>y>abs(x) else "no") rint("y" if abs(x)<1 and 1>y>abs(x) else "no")
Задание
Выясните принадлежность точки А(х,у)
к области, ограниченный линиями
y = 0, x = 3, y = x2
Метод Монте-Карло
Площадь произвольной фигуры можно вычислить методом Монте-Карло. Фигура вписывается в другую фигуру с известной площадью. Случайным образом на последнюю ставятся произвольное количество точек. Площадь определяется по формуле S=Sф*Nф/N, где Nф – количество точек попавших в заданную фигуру, N – общее количество точек, Sф – площадь заданной фигуры.
Определение площади шара, методом Монте-Карла.

import random
m = 0
n = 10000 # всего точек
r = 100 # радиус
for i in range(n):
x = random.randint(0,r+1)-r
y = random.randint(0,r+1)-r
z = random.randint(0,r+1)-r
if x**2+y**2+z**2 <= r**2:
m+=1
print("monte-karlo", (2*r)**3*m/n)
print("analitik",3.14*4/3*(r**3))
Определение числа π
Например, если мы будем случайным образом «бросать» на плоскость точки (случайно выбирать координаты x и y), то чем больше площадь фигуры, тем больше на нее попадёт точек. Если при этом число «бросков» стремится к бесконечности, то отношение количества точек, попавших на две фигуры, будет стремиться к отношению площадей этих фигур.
Для простоты вычисления возьмём четверть такого круга, лежащую в I квадранте Декартовой плоскости, а потом умножим результат на 4.
Площадь круга равна π*R2. Площадь квадрата R2 Значит, чтобы вычислить число π, достаточно поделить первое на второе. Координаты x и у будут меняться в диапазоне [0, 1].
i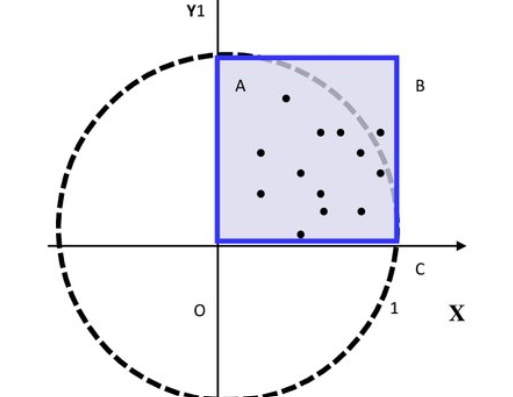 mport random mport random
k = 0.0
n = 500000
for i in range(n):
x = random.random()
y = random.random()
k += (x * x + y * y < 1.0)
print(4 * k / n)
Задание
Найдите тем же способом площадь круга радиусом 10. Изменив n, выясните как меняется точность вычисления.
|
Дан действительный радиус круга R и размер клетки L на клеточной бумаге. Известно, что центр круга находится на пересечении линий. Требуется найти число целых клеток, лежащих внутри круга. 0 ≤ R ≤ 25000, 1 < L < 100.

import math
R = 10
L = 5
i = L
count=0
if L > R*math.sqrt(2):
print(0)
else:
while i <= R:
j = L
r = math.sqrt(R**2-i**2)
while j <= r:
count+=1
j+=L
i+=L
print(count*4)
|
Рассматривается множество целых чисел, принадлежащих отрезку [1045; 8963], которые делятся на 5 или на 7 и не делятся на 11, 13, 17 и 19. Найдите количество таких чисел и минимальное из них. В ответе запишите два числа через пробел: сначала количество, затем минимальное число
def F(n): return (n%5 == 0 or n%7 == 0) and \
n%11 and n%13 and n%17 and n%19
a = [ n for n in range(1045, 8963) if F(n) ]
print(len(a), a[0])
1867 1050
|

count = 0
def from10ss(x, ss):
t = 1
d = 0
while x > 0:
d = d + (x % ss) * t
t = t * 10
x = x // ss
return d
a = 531441 #1000000
b = 4782968 #8888888
for i in range(a,b+1):
s = from10ss(i, 9)
if s//1000000 !=2 and s//1000000 !=6 and s%10 != (s%100)//10:
count +=1
print(count)
|

|
Реализация графов и деревьев на Python / Хабр (habr.com)
inf-2014-10.pdf (kpolyakov.spb.ru)
|
Справочник Знаки в программировании
Присваивание ( = ), пример: Х = 5 ( икс присвоить пять)
Равенство: ( == ), пример: 100 == 100
Деление: ( / ), пример: 5 / 2 будет 2.5
Целая часть от деления ( // ), пример: 5 // 2 будет 2
Остаток от деления ( % ), пример: 5 % 2 будет 1
Умножение ( *), пример: 2*3 будет 6
Сложение (+), пример: 2 + 2 будет 4
Склеивание (+), пример: ‘2’ + ‘2’ будет ’22’
Вычитание ( - ), пример: 0 - 3 будет -3
Знаки неравенства
Равно ( == )
Больше (>)
Меньше (<)
Не больше ( <=)
Не меньше (>=)
Не равно ( != )
L = 2 == 2
Пояснение: логическая переменная L присваивает выражение «2==2» (два равно два). L= 2 == 2 будет True (истина)
L = 2 < 2 будет False (ложь)
L = 2 * 2 == 4
print('yes' if L = True else 'no')
Пояснение:
Логическая переменная L присваивает выражение: «2 *2 == 4» (дважды два четыре)
Печатаем да если L истинна, иначе печатаем нет.
Можнокороче:
L = 2 * 2 == 4
print('yes' if L else 'no')
Ещёкороче:
print( 'yes' if 2*2==4 else 'no‘ )
Логические связки
Или ( or )
И ( and )
Не ( not )
Примеры:
Если первая цифра и вторая цифра числа n не больше 5:
n//10<=5 and n%10<=5
Если первая цифра числа n не равно 5 или 0:
n//10!=5 or n // 10!=0
То же самое:
not(n//10==5) or not(n // 10) == 0
Задачи на логические связки
ИзучитеЗнаки неравенства и Логические связки
На вход программы поступает произвольное двузначное число, проверить:
начинается ли оно с цифры 2
оканчивается ли оно цифрой 1
равна ли сумма цифр 3
меньше ли первая цифра 5
не меньше ли вторая цифра 6
не равно ли вторая цифра 0
не превышают ли цифры числа 4
Есть ли хотя бы одна цифра равная 5
Есть ли хотя бы одна цифра равная 5 или 6?
Равны ли первая и вторая цифры 5 или 6?

Ссылки
Школа программиста (acmp.ru)
Online Python - IDE, Editor, Compiler, Interpreter (online-python.com)
Online Python Compiler - online editor (onlinegdb.com)
|
 Скачать 7.93 Mb.
Скачать 7.93 Mb.











 rint("y" if abs(x)<1 and 1>y>abs(x) else "no")
rint("y" if abs(x)<1 and 1>y>abs(x) else "no")
 mport random
mport random


