Теория графов
Урок 3.24
Граф это вершины соединенные ребрами.
Графы бывают ориентированные (орграф) и неориентированные, взвешенные и не взвешенные.
Дерево это разновидность орграфа, который не имеет циклов
Матрица смежности:
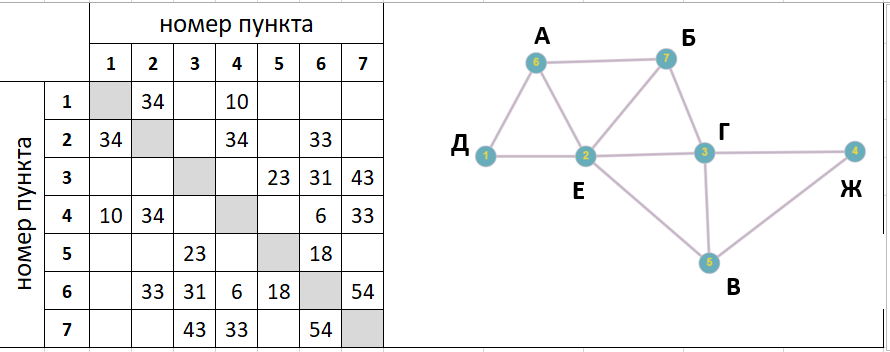
Дан граф, создать его матрицу смежности
Граф задается следующим образом: в первой строке записано число вершин n и число ребер m графа. Далее записаны m строк, содержащих по два числа – номера начальной и конечной вершины ребра.
5 7
1 2
2 5
5 4
4 2
1 4
1 3
3 4
Если граф неориентированный, то матрица смежности всегда симметрична относительно главной диагонали.
n, m = map(int, input().split())
A = [[0] * (n + 1) for i in range(n + 1)]
for i in range(m):
u, v = map(int, input().split())
A[u][v] = 1
A[v][u] = 1
for i in range(n):
for j in range(n):
print(A[i][j], end=' ')
print()
Строчку A[v][u] = 1 нужно закомментировать в случае ориентированного графа.
Пример работы
5 2
1 2
3 4
0 0 0 0 0
0 0 1 0 0
0 1 0 0 0
0 0 0 0 1
0 0 0 1 0
Задание
Создайте матрицу смежности для орграфа:
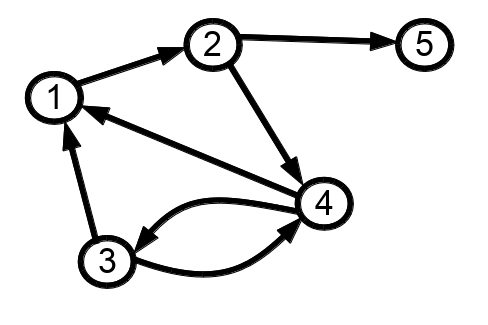
|
Урок 3.25
Списки смежности матрицы
W [1] = [2] [1] = [2]
W[2] = [4, 5]
W[3] = [1, 4]
W[4] = [1, 3]
W[5] = []
Пример заполнения списков смежности, используются множества вместо списков:
n, m = map(int, input().split())
W = [set() for i in range(n + 1)]
for i in range(m):
u, v = map(int, input().split())
W[u].add(v)
# W[v].add(u)
for i in range(n):
print("W(",*W[i],")")
Задание
Создайте списки смежности для матрицы
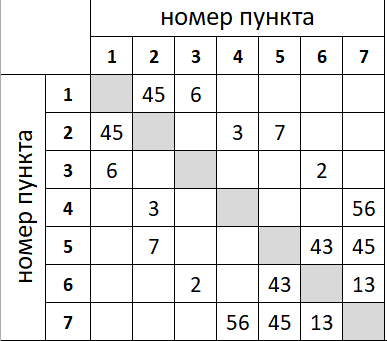
|
Урок 3.26 Взвешенные графы
При представлении графа матрицей смежности вес ребра можно хранить в матрице, то есть A[i][j] в данном случае будет равно весу ребра из i в j. При этом при отсутствии ребра можно хранить специальное значение, например, None. Во многих задачах удобно при отсутствии ребра хранить очень большое число, в этом случае отсутствие ребра аналогично наличию ребра очень большой стоимости.
Степень графа

Задание создайте взвешенный граф и выведите его на экран, найдите степени вершин

| |
 Скачать 7.93 Mb.
Скачать 7.93 Mb.