практикумы по языку Питон. Питон. Практикум Загидуллин Наиль Рашитович мбоу сош 2 Оглавление Введение в Питон 4 Команда вывода 4

• Название: Практикум Загидуллин Наиль Рашитович мбоу сош 2 Оглавление Введение в Питон 4 Команда вывода 4
• Анкор: практикумы по языку Питон
• Дата: 07.11.2022
• Размер: 7.93 Mb.
• Имя файла: Питон.docx
• Тип: Практикум; #774704
• страница: 6 из 11

Структурные типы. Массивы

Файл можно открыть и так:
with open('input.txt') as file:

#обработка файла

file.read(n)	чтение первых n символов файла
file.readline()	читает одну строчку строки или файла
file.readlines()	читает и возвращает список всех строк в файле

Разные задачи

Задание: Решите эту задачу, но числа а,b,c считываются с входного файла: 1) построчно Пример 3 6 9 2) в одну строку Пример 4 8 2

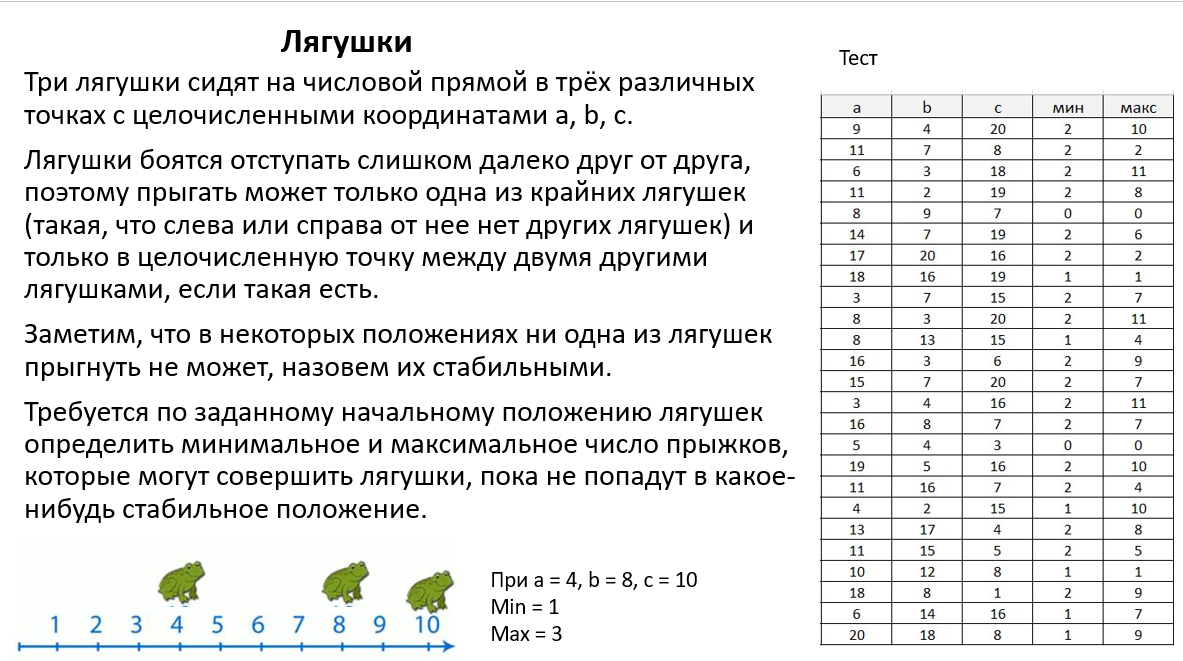
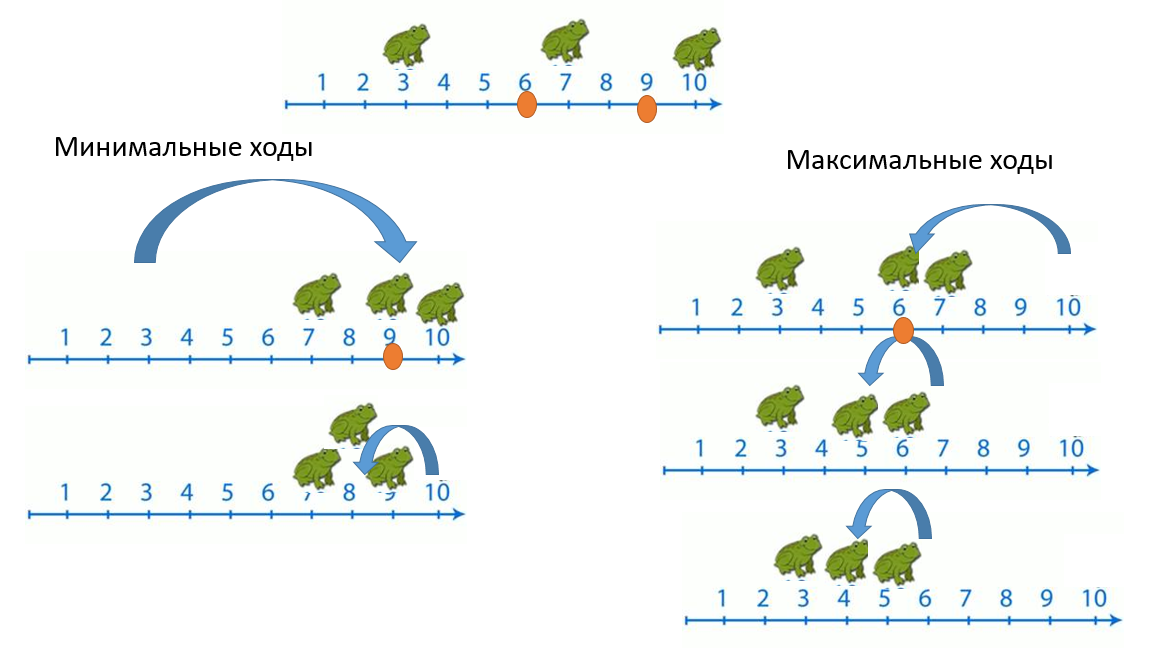
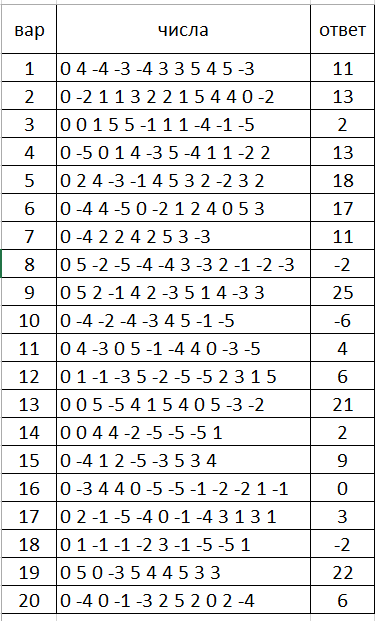
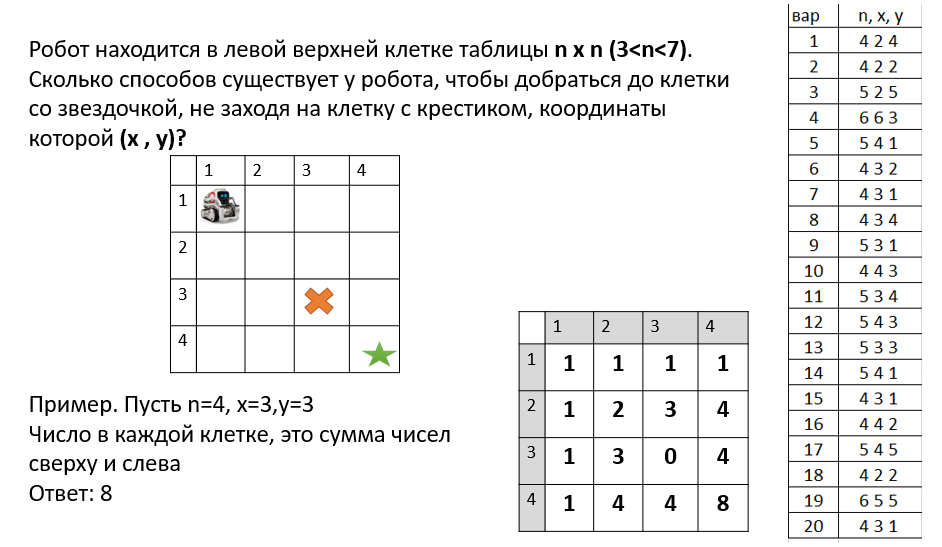
3. Методы решения сложных задач в программировании

Динамическое программирование

https://mipt-cs.github.io/python3-2017-2018/labs/lab11.html

Урок 3.1 Классическая задача — числа Фибоначчи

Последовательность Фибоначчи Fn задается формулами: F1 = 1, F2 = 1, Fn = Fn – 1 + Fn – 2 при n > 1. Необходимо найти Fn по номеру n.

Один из способов решения, который может показаться логичным и эффективным, — решение с помощью рекурсии:

def fib(n):

if n <= 1:

return n

else:

return fib(n-1) + fib(n-2)

Но уже при n = 40 программа работает заметно долго. Это связано с тем, что одни и те же промежуточные данные вычисляются по несколько раз — число операций нарастает с той же скоростью, с какой растут числа Фибоначчи — экспоненциально.

Один из выходов из данной ситуации — сохранение уже найденных промежуточных результатов с целью их повторного использования (кеширование):

def fib(n):

F = [-1]*(n+1)

F[0] = 0

F[1] = 1

for i in range(2, n+1):

F[i] = F[i - 1] + F[i - 2]

return F[n]

print(fib(45))

Используя динамическое программирование решите задачи. Примените оба способа (простой и с кэшированием) и протестируйте программу для больших чисел.

1 Кузнечик. На числовой прямой сидит кузнечик, который может прыгать вправо на одну или на две единицы. Первоначально кузнечик находится в точке с координатой 1. Определите количество различных маршрутов кузнечика, приводящих его в точку с координатой n

2 Лестница. Таня может спуститься вниз по лестнице, делая 1 шаг вниз по ступеньке, либо через одну. Сколько имеется способов у Тани спуститься вниз по лестнице, если количество ступенек n?

Урок 3.2 Задачи про Робота (динамическое программирование):

Робот