Геометрия 7. Праскова мария валериевна учитель математики мбоу гундинская сош

• Название: Праскова мария валериевна учитель математики мбоу гундинская сош
• Анкор: Геометрия 7
• Дата: 27.09.2022
• Размер: 0.71 Mb.
• Имя файла: 944973b0a653cebb4a487dc08d088479 3.docx
• Тип: Документы; #699790
• страница: 5 из 6

§ 1. СУММА УГЛОВ ТРЕУГОЛЬНИКА

В результате изучения параграфа 1 учащиеся должны уметь доказывать теорему о сумме углов треугольника и ее следствия; знать, какой угол называется внешним углом треугольника, какой треугольник называется остроугольным, тупоугольным, прямоугольным; уметь решать задачи типа № 223, 224, 225, 226, 228, 229, 234.

Урок 1. ТЕОРЕМА О СУММЕ УГЛОВ ТРЕУГОЛЬНИКА

 Цели: доказать теорему о сумме углов треугольника, следствия из нее; ввести понятия остроугольного, прямоугольного и тупоугольного треугольников; рассмотреть задачи на применение доказанных утверждений.

I.  Анализ результатов контрольной работы.

1. Проанализировать характерные ошибки, допущенные в контрольной работе.

2. Выполнить работу над ошибками.

 II. Изучение нового материала.

1. Решить задачу по готовому чертежу на доске (см. рис.).

На рисунке ВД || АС.

Найдите сумму углов треугольника ABC.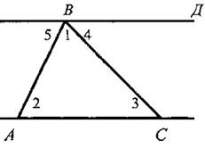

 

 2. Вслед за решением этой задачи перед учащимися ставится вопрос: случайно ли сумма углов данного треугольника ABC оказалась равной 180° или этим свойством обладает любой треугольник?

Поиск ответа естественно приводит к формированию теоремы о сумме углов треугольника.

3. Доказательство теоремы о сумме углов треугольника (рис. 124 учебника).

4. Устно решить задачи № 223 (а, б, г), 225, 226.

5. Перед введением классификации треугольников по углам (п. 31) учащимся задается вопрос: «Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один прямой и один тупой угол?».

Ответы должны быть обоснованы с помощью теоремы о сумме углов треугольника.

6. Записать в тетрадях вывод из этих ответов (следствие из теоремы о сумме углов треугольника): в любом треугольнике либо все три угла острые, либо два угла острые, а третий — тупой или прямой.

7. Ввести понятия остроугольного, тупоугольного и прямоугольного треугольников и обратить внимание учащихся на названия сторон прямоугольника, треугольника - гипотенуза и катет (рис. 126 учебника, модели треугольников).

 III. Закрепление изученного материала.

1. Решить задачи № 227(a) и 224 на доске и в тетрадях.

2. Решить задачу № 228 (а, в) на доске и в тетрадях.

Решение

1) Рассмотрим два случая:

а) угол при основании равен 40°, тогда второй угол при основании равнобедренного треугольника тоже равен 40°; значит, угол при вершине равен 180° - (40° + 40°) = 100°;

б) угол при вершине равен 40°, тогда углы при основании равны (180° - 40°) : 2 = 70°.

Ответ: 40°; 40° и 100° или 40°; 70°.

2) Опираемся на доказанное в задаче № 226 утверждение: углы при основании равнобедренного треугольника острые. Значит, угол при вершине равен 100°, а углы при основании равны (180° - 100°) : 2 = 40°.

Ответ: 100°; 40° и 40°.

3. Решить задачу № 229 на доске и в тетрадях.

 

IV. Итоги урока.

Домашнее задание: изучить пункты 30-31; ответить на вопросы 1; 3; 4; 5 на с. 89; решить задачи № 223 (б), 228 (б), 230.

Урок 2. ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. ТЕОРЕМА О ВНЕШНЕМ УГЛЕ ТРЕУГОЛЬНИКА

 Цели: закрепить знания учащихся о сумме углов треугольника при решении задач; ввести понятие внешнего угла треугольника; доказать теорему о внешнем угле треугольника; учить решению задач.

Ход урока

1. Проверка усвоения изученного материала.

1. Один учащийся на доске доказывает теорему о сумме углов треугольника.

2. Второй учащийся решает на доске задачу № 230.

3. Устно со всем классом решаем задачи по готовым чертежам.

Вычислите все неизвестные углы треугольника (по рис. 1-8).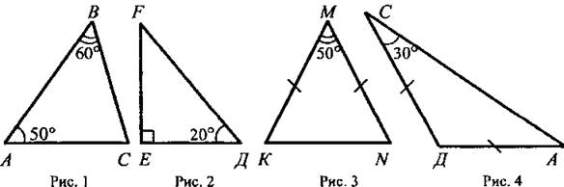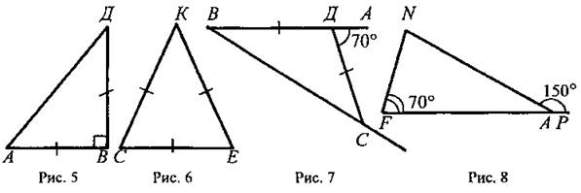

 



 



 

II. Изучение нового материала.

1.  Ввести понятие внешнего угла треугольника.

2.  Доказать теорему о внешнем угле треугольника (рис. 125 учебника).

3.  Устно решить задачу: в треугольнике ABC ∠В = 110°. Чему равны: а) сумма остальных внутренних углов треугольника? б)           внешний угол при вершине В?

4 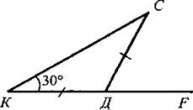.  По готовому чертежу на доске устно решить задачу:

Найдите внутренние и внешний угол СДF треугольника КСД.

 III. Решение задач.

1.  Решить задачу № 232 под руководством учителя на доске и в тетрадях.

Дано: ∠CBE — внешний угол треугольника ABC; ∠CBE = 2∠A.

Доказать: ΔАВС — равнобедренный.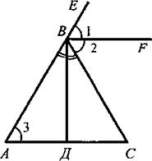

 

Решение: Проведем биссектрисы BF и ВД смежных углов СВЕ и ABC, тогда ВЕ ⊥ ВД (см. задачу № 83). BF || АС, так как ∠1 = ∠2 = ∠3. а углы 1 и 3 соответственные при пересечении прямых BF и АС секущей АВ. ВД ⊥ АС, так как ВД ⊥ BF, a BF || AC. В треугольнике ABC биссектриса ВД является высотой, следовательно, треугольник ABC - равнобедренный (см. задачу № 133).

2. Обратное утверждение также верно, а именно: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании. Действительно, этот внешний угол равен сумме двух углов при основании равнобедренного треугольника, а так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника.

3. Решить задачу № 234 на доске и в тетрадях (рассмотреть два случая).

 IV. Самостоятельная работа обучающего характера (15-20 мин).

Вариант I

1. Один из углов равнобедренного треугольника равен 96°. Найдите два других угла треугольника.

2. В треугольнике СДЕ с углом ∠E = 32° проведена биссектриса CF, ∠СFД = 72°. Найдите ∠Д.

Вариант II

1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла треугольника.

2. В треугольнике СДЕ проведена биссектриса CF, ∠Д = 68°, ∠Е = 32°. Найдите ∠CFД.

Вариант III

1. В равнобедренном треугольнике MNP с основанием МР и углом ZN= 64° проведена высота МН. Найдите АРМН.

2. В треугольнике СДЕ проведены биссектрисы СК и ДР, пересекающиеся в точке F, причем ZДРК = 78°. Найдите /.СЕД.

Вариант IV

1. В равнобедренном треугольнике СДЕ с основанием СЕ и ∠Д = 102° проведена высота СН. Найдите ∠ДСН.

2. В треугольнике ABC проведены биссектрисы AM и BN, пересекающиеся в точке К, причем ∠AKN = 58°. Найдите ∠ACB.

 

V. Итоги урока.

Домашнее задание: изучить пункты 30-31; ответить на вопросы 1-5 на с. 89; решить задачи № 233, 235

СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА (§ 2)

Урок 1. ТЕОРЕМА О СООТНОШЕНИЯХ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА

 Цели: рассмотреть теоремы о соотношениях между сторонами и углами треугольника, следствия из этих теорем; научить применять эти знания при решении задач.

I. Анализ результатов самостоятельной работы.

 II. Изучение нового материала.

1 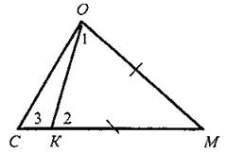. Изучение нового материала необходимо начать с решения подготовительной задачи (см. рис.).

Дано: ΔМОС; КМ = ОМ; К ∈ МС.

Доказать: 1) ∠1 > ∠3; 2) ∠MOC > ∠3.

 Доказательство: 1) Треугольник ОМК - равнобедренный с основанием ОК, поэтому ∠1 = ∠2. Угол 2 - внешний угол треугольника ОКС, поэтому ∠2 > ∠3. Значит, ∠1 = ∠2 и ∠2 > ∠3, следовательно, ∠1 > ∠3.

2) Так как точка К лежит на МС, то ∠MOC > ∠1, а так как ∠1 > ∠3, то ∠MОC > ∠3.

2. Сформулировать и доказать первое утверждение теоремы: в треугольнике против большей стороны лежит больший угол (по рис. 127 учебника).

3. Устно решить задачу № 236.

4. Перед доказательством второго утверждения теоремы (в треугольнике против большего угла лежит большая сторона) напомнить учащимся, какая теорема называется обратной данной, и предложить привести примеры обратных теорем, изученных ранее.

5. Дать возможность учащимся самостоятельно сформулировать утверждение, обратное первому утверждению. На классной доске и в тетрадях учащиеся делают следующую запись:

	Теорема	Обратная теорема
Дано (условие)	ΔАВС; АВ > АС	ΔАВС; ∠АСВ > ∠АВС
Доказать (заключение)	∠ACB > ∠АВС	АВ > АС

 6. Доказательство обратного утверждения проводится методом от противного. В связи с этим, после того как сформулирована обратная теорема, записаны ее условие и заключение, полезно вспомнить, что при сравнении двух отрезков, например, СД и EF, возможен один и только один из трех случаев: СД > EF; СД = EF; СД < EF. Поэтому если мы предполагаем, что СД не больше EF, то возможны два случая: либо СД = EF, либо СД < EF. После этих предварительных рассуждений учащимся легче понять, почему при доказательстве теоремы, предположив, что АВ не больше АС, мы рассматриваем два возможных случая: либо АВ = АС, либо АВ < АС.

7. Устно решить задачу № 237.

8. Следствие 1 учащиеся доказывают самостоятельно.

9. Следствие 2, выражающее признак равнобедренного треугольника, учащиеся доказывают с помощью учителя.

 

III. Закрепление изученного материала.

1. Решить следующие задачи (по готовым чертежам):

1) В треугольнике ABC угол С тупой, К - произвольная точка на стороне АС. Докажите, что ВК < АВ.

2) В треугольнике ABC на стороне АС отмечена точка Д так, что ДС = ВС. Докажите, ∠В > ∠A.

2. Решить задачу № 240.

 IV. Итоги урока.

Домашнее задание: изучить п. 32; ответить на вопросы 6-8 на с. 89-90; решить задачи № 239, 241.

 Урок 2. НЕРАВЕНСТВО ТРЕУГОЛЬНИКА

 Цели: доказать теорему о неравенстве треугольника; учить решать задачи, используя изученные теоремы и следствия из них; развивать логическое мышление учащихся.

I. Проверка усвоения изученного на предыдущем уроке материала.

1. Фронтальный опрос.

2. Два человека записывают в это время на доске решения домашних задач для последующей проверки с классом.

 

II. Объяснение нового материала.

1. Доказательство теоремы о неравенстве треугольника.

2. Решение задачи № 251 (есть решение в учебнике на странице 75).

После этого записать в тетрадях вывод: Каждая сторона треугольника меньше суммы двух других сторон, но больше разности двух других сторон: в – с < а < в + с; а – с < в < а + с; а – в < с < а + в.

3. Устно решить задачу № 248.

 

III. Решение задач.

1. Решить задачу № 249.

Решение

Рассмотрим два случая:

1) стороны равнобедренного треугольника 25 см, 25 см и 10 см. По теореме о неравенстве треугольника имеем:

25 < 25 + 10 верное.

25 < 35 верное.

Значит, основание равно 10 см;

2) стороны равны 10 см, 10 см и 25 см. По теореме о неравенстве треугольника получим 25 < 10 + 10; 25 < 20 неверное.

Ответ: основание равно 10 см.

2. Самостоятельно решить задачу № 250 (а).

3. Решить задачу № 253 на доске и в тетрадях.

Решение

1) Пусть внешний угол при вершине А равнобедренного треугольника ABC острый, тогда ∠BAC тупой. Следовательно, ВС - основание треугольника, а потому ∠B = ∠C и АВ = АС.

2) ВС > АВ и ВС > АС, так как против тупого угла лежит большая сторона треугольника. Поэтому, учитывая условия задачи, имеем: ВС - АВ = 4 (см), отсюда ВС = АВ + 4.

3) АВ + АС + ВС = 25 см, или 2АВ + ВС = 25 см.

Но ВС = АВ + 4, тогда 2АВ + АВ + 4 = 25;

3АВ = 21; АВ = 7 см, ВС = 11 см, АС = 7 см.

Ответ: 7 см, 11 см, 7 см.

4. Решить задачу № 246 по рисунку 129 учебника на доске и в тетрадях.

 

IV. Итоги урока.

Домашнее задание: выучить материал пунктов 30-33; ответить на вопросы 1-9 на с. 89-90; решить задачи № 242, 250 (б, в).



Урок 3. РЕШЕНИЕ ЗАДАЧ

 Цели: повторить и обобщить изученный материал; выработать умение учащихся применять изученные теоремы при решении задач; развивать логическое мышление учащихся; подготовить учащихся к контрольной работе.

I.  Актуализация опорных знаний учащихся.

1. Проверка доказательства теоремы о соотношениях между сторонами и углами треугольника и теоремы о неравенстве треугольника (у доски и за первыми партами - на листочках; это позволяет проверить у учащихся знание теорем и накопить отметки).

2. Фронтальная работа с классом:

1) ответы на вопросы 1-9 на с. 89-90;

2) устно решить задачу: существует ли треугольник со сторонами 4 м, 5 м и 8 м; со сторонами 6 см, 12 см и 3 см; со сторонами 9 дм, 9 дм и 7 дм?

3. Собрать листочки у работающих на месте и выслушать ответы учащихся, работающих у доски.

 

II. Решение задач.

1. Решить задачу № 243 на доске и в тетрадях.

Дано: ΔABC; АА1 - биссектриса; СД || АА1 и Д ∈ АВ.

Доказать: АС = АД.

 

Доказательство: Так как по условию АА1 - биссектриса треугольника ABC, то ∠1 = ∠2.

∠1 = ∠4 как накрест лежащие углы при пересечении параллельных прямых АА1 и СД и секущей АД. Из равенств ∠1 = ∠2; ∠1 = ∠4; ∠2 = ∠3 следует, что ∠3 = ∠4, тогда по признаку равнобедренного треугольника имеем, что треугольник ДАС - равнобедренный, значит, по определению АС = АД.

2. Решить задачу 1: в прямоугольном треугольнике ABC гипотенуза АВ = 10 см. Найдите СД, если точка Д лежит на гипотенузе АВ и ВД = СД.

Д 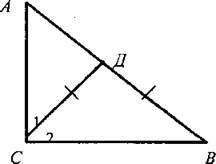ано: ДABC; ∠С = 90°; АВ = 10 см. Д ∈ АВ и ВД = СД

Найти: СД.

Решение: ∠2 = ∠5, так как по условию СД = ДВ. ∠1 + ∠2 = 90°; ∠В + ∠А = 90°; но ∠2 = ∠В, поэтому ∠А = ∠1, значит, треугольник АДС - равнобедренный, тогда АД = СД.

Итак, СД = ВД по условию, АД = СД по доказанному, следовательно, СД = 1/2АВ = 5 см.

Ответ: 5 см.

3. Решить задачу 2: отрезок ЕК — биссектриса треугольника ДЕС.

Докажите, что КС < ЕС.

 Урок 4. КОНТРОЛЬНАЯ РАБОТА № 4 (1 час)

 Цели: проверить знания и умения учащихся в решении задач и применении изученного материала.

I.  Организация учащихся на выполнение работы.

 II. Выполнение работы по вариантам.

В 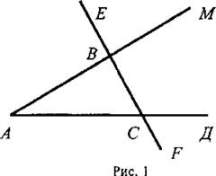ариант I

1. На рисунке 1 ∠ABE = 104°, ∠ДCF = 76°, АС = 12 см. Найдите сторону АВ треугольника ABC.

 2. В треугольнике СДЕ точка М лежит на стороне СЕ, причем ∠СМД - острый. Докажите, что ДЕ > ДМ.

3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.

В ариант II

1. На рисунке 2 ∠BAE = 112°, ∠ДВF = 68°, BС = 9 см. Найдите сторону АС треугольника ABC.

 2. В треугольнике MNP точка К лежит на стороне MN, причем ∠NKP - острый. Докажите, что КР < МР.

3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

Вариант III (для более подготовленных учащихся)

1. На рисунке 1 ∠CBM = ∠ACF; РΔABC = 34 см, ВС = 12 см. Найдите сторону АС треугольника ABC.

2. В треугольнике MNK ∠K = 37°, ∠M = 69°, NP - биссектриса треугольника. Докажите, что МР < РК.

3. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой па 12 см. Найдите стороны треугольника.

Вариант IV (для более подготовленных учащихся)

1. На рисунке 2 ∠EAM = ∠ДBF; ВС = 17 см, РΔABC = 45 см. Найдите сторону АВ треугольника ABC.

2. В треугольнике СДЕ ∠E = 76°, ∠Д = 66°, ЕК - биссектриса треугольника. Докажите, что КС > ДК.

3.  Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найдите стороны треугольника.

 IV. Итоги урока.

ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ (§ 3)

Урок 1. НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

 Цели: рассмотреть некоторые свойства прямоугольных треугольников и показать, как они применяются при решении задач.

I.  Анализ результатов контрольной работы.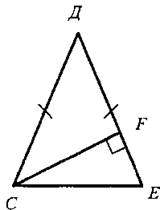

  II. Изучение нового материала.

1.  Устно решить задачу № 254 (использовать демонстрационный равнобедренный прямоугольный треугольник).

2. Решить задачу № 255 на доске и в тетрадях.

Дано: ΔСДЕ; СД = ДЕ; CF ⊥ ДЕ; ∠Д = 54°.

Найти: ∠ECF.

Решение:

По условию треугольник СДЕ - равнобедренный, тогда ∠Е = ∠ДСЕ = (180° - 54°) : 2 = 63° (углы при основании равнобедренного треугольника равны).

Так как CF ⊥ ДЕ по условию, то треугольник CFE - прямоугольный, в нем ∠CFE = 90°, ∠Е = 63°; тогда ∠ECF = 180° - (90° + 63°) = 27°.

Ответ: 27°.

3. Рассмотреть свойство 1° и посоветовать учащимся запомнить его, поскольку оно часто используется при решении задач.

4. Доказательство свойств 2° и 3° следует провести учителю самому с записью условия и заключения прямого и обратного утверждений на доске в виде таблицы. Эту таблицу учащиеся должны воспроизвести в своих тетрадях.

 

	Теорема	Обратная теорема
Дано	ΔABC; ∠A = 90°          ∠B = 30°	ΔABC; ∠A = 90° АС = 1/2ВС
Доказать	АС = 1/2ВС	∠B = 30°

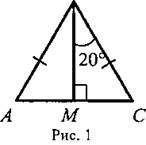  III. Закрепление изученного материала.

1. Устно решить задачи по готовым чертежам на доске:

1) Дано: ΔАВС (рис. 1).

Найти: углы ΔАВС.

 2) Дано: a || в (рис. 2).

Найти: углы треугольника MON.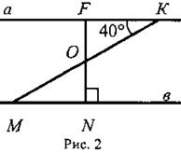

  2. Решить задачу № 257 на доске и в тетрадях.

Дано: ΔАВС (рис. 3); ∠C = 90°, ∠ВАД = 120° - внешний угол; АС + АВ = 18 см.

Найти: АС и АВ.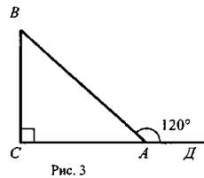

  Решение:

∠CAB = 180° - 120° = 60° (смежные углы), тогда ∠B = 90° - 60° = 30° (по свойству 1°); АС = 1/2AВ (свойство 2°; катет, лежащий против угла в 30°). По условию АС + АВ = 18 см; 1/2АВ + АВ = 18 см; 1 · 1/2AB = 18 см, АВ = 12 см; значит, АС = 18 - 12 = 6 (см).

Ответ: АВ = 12 см; АС = 6 см.

3. Решить задачу № 260.

Д 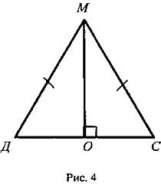ано: ΔДМС (рис. 4); ДМ = МС; МО ⊥ ДС; ДМ = 15,2 см; МО = 7,6 см.

Найти: углы ΔДМС.

Решение:

Так как МО = 1/2ДМ, то по свойству 3° ∠Д = 30°, тогда ∠C = 30°, ∠M = 180° - (30° + 30°) = 180° - 60° = 120°.

Ответ: ∠Д = ∠C = 30°; ∠М = 120°.

 IV. Итоги урока.

Домашнее задание: изучить п. 34; повторить пункты 15—33; ответить на вопросы 10 и 11 на с. 90; решить № 256, 259.