Пределы. Последовательност. Пределы последовательности
 Скачать 340.47 Kb. Скачать 340.47 Kb.
|
|
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗАВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН АНДИЖАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ ЗАХИРИДДИНА МУХАММАДА БАБУРА ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ НАПРАВЛЕНИЕ МАТЕМАТИКА КУРСОВАЯ РАБОТА На тему: Пределы последовательности Студентки курса Усманова Гулбахора Научный руководитель: Дехконов.Ж  Андижан-2020год ANDIJON DAVLAT UNIVERSITETI Talabaning kurs ishlarini ochiq ximoya qilish xay’atyi g’ilishining YOZMA BAYONNOMASI №___________________________________________________ Qatnashdi: xay’atazolari, kurs ishi yozgan talabalar kurs ishi Talaba_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Savollar___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Javoblar:_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Fakultetning__________________bo’limi________kurstalabasi____________________ning _____________________________________________________________________________ kafedrasida__________________________________fan bo’yicha________________________ _____________________________________________________________________________ Mavzusidayozilgankursishiningsifatixaqida. ОГЛАВЛЕНИЕ ВВЕДЕНИЕ 2.1 Предел последовательности комплексных чисел. Предел и непрерывность функции комплексного переменного. 2.2 Дифференцирование функции комплексного переменного. Условия Коши-Римана. 3. ЗАКЛЮЧЕНИЕ 4. Список использованной литературы ВВЕДЕНИЕ Современная педагогическая и информационная в Национальной программе подготовки кадров разработка и внедрение технологий особое внимание уделяется. Конечно, хотя и медленно, В учебный процесс внедряется ряд новых педагогических технологий. Тем не менее, есть еще много важных вопросов, которые необходимо решить. Есть проблемы, которые огромны для наших педагогов обязанности. В настоящее время преподаватели имеют высокий уровень профессиональной подготовки, педагогический мастерство, высокие духовно-нравственные качества, глубокие идеологии знания, современная педагогика в воспитательной работе Эффективное использование технологий, интерактивных методов является требованием периода рассчитывается. Молодое поколение зрелое, знающее, высоко духовное, чтобы они росли, чтобы быть компетентными, патриотичными людьми как самое важное звено в проводимой огромной творческой работе высокие научные, методические и практические знания педагогических кадров чтобы убедиться, что у них есть навыки высокой производительности это принять необходимые меры. Этот вопрос обсуждался с первых лет независимости серьезное внимание уделяется. Об этом заявил первый президент И.А. Каримов четко выражены следующие взгляды: «Школы и образование находятся под контролем государства и общества закреплено в нашем Основном законе. Тем не менее, это широкий общественность, участие и поддержка всех наших людей является общим вопросом, который требует »(И.А. Каримов. Высокая духовность является непобедимой силой. - Т.:« Духовность », 2008. С. 61). Закон Республики Узбекистан "Об образовании" и обучении Реализация национальной программы - это переход к многоуровневой системе образования, квалифицированной программы бакалавриата и магистратуры в высшем и среднем образовании несет огромную ответственность перед профессорами и преподавателями, которые там работают загружает задачи. В данной курсовой работе рассматривается тема пределы последовательности, рассматриваются свойства данных последовательности, даны определения, решены некоторые задачи относящиеся к данной теме. Предел последовательности комплексных чисел. Предел и непрерывность функции комплексного переменного. 1.1. Пусть дана последовательность комплексных чисел 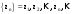 Комплексное число а называется пределом последовательности 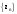 , если для любого положительного числа ε можно указать такой номер , если для любого положительного числа ε можно указать такой номер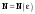 , начиная с которого все члены , начиная с которого все члены 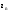 этой последовательности удовлетворяют неравенству этой последовательности удовлетворяют неравенству 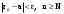 . . Последовательность 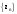 , имеющая предел а, называется сходящейся к числу а, что записывается в виде , имеющая предел а, называется сходящейся к числу а, что записывается в виде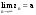 . .Каждой последовательности комплексных чисел 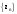 соответствуют две последовательности действительных чисел соответствуют две последовательности действительных чисел 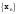 и и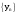 , где , где 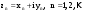 ТЕОРЕМА 1. Последовательность 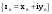 сходится к числу сходится к числу 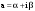 тогда и только тогда, когда тогда и только тогда, когда 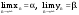 Последовательность 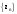 называется ограниченной, если существует положительное число М такое, что для всех элементов называется ограниченной, если существует положительное число М такое, что для всех элементов 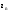 этой последовательности выполняется неравенство этой последовательности выполняется неравенство 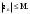 ТЕОРЕМА 2. Всякая сходящаяся последовательность 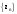 ограничена. ограничена.Свойства сходящихся последовательностей. Если 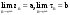 , то , то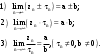 Пример. 1.1. Доказать, что последовательность 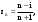 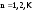 имеет пределом число а = 1. имеет пределом число а = 1.Доказательство. Пусть задано произвольное число ε > 0. Покажем, что существует такой номер N, что 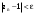 для всех n для всех n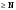 . Так как . Так как 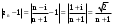 , ,то неравенство 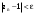 будет выполнено, если будет выполнено, если 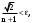 т. е. при т. е. при 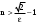 . Значит, в качестве . Значит, в качестве 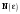 можно взять число можно взять число 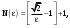 где символ 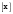 означает целую часть действительного числа x. означает целую часть действительного числа x.Достаточное условие сходимости последовательности комплексных чисел. Пусть 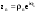 , где , где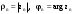 . Тогда, если . Тогда, если 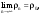 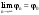 , то , то 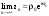 . .Примеры. 1.2. Доказать, что 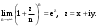 Доказательство. Обозначим 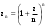 . Тогда . Тогда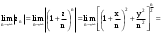 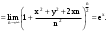 Так как 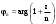 = =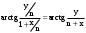 , , то 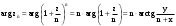 . .Значит, 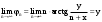 . .Пользуясь достаточным условием сходимости последовательности комплексных чисел, получим 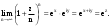 1.3. Доказать, что последовательность 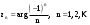 расходится. расходится.Доказательство. Так как 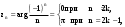 то последовательность 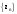 имеет вид: π; 0; π; 0; … и предела не имеет. имеет вид: π; 0; π; 0; … и предела не имеет.Пусть имеем последовательность 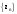 комплексных чисел комплексных чисел 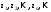 Если для любого сколь угодно большого числа М > 0 существует натуральное число N такое, что все члены zn последовательности с номерами n > N удовлетворяют неравенству |zn | > M, то говорят, что последовательность Если для любого сколь угодно большого числа М > 0 существует натуральное число N такое, что все члены zn последовательности с номерами n > N удовлетворяют неравенству |zn | > M, то говорят, что последовательность 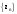 сходится к бесконечно удалённой точке или к бесконечности: сходится к бесконечно удалённой точке или к бесконечности: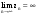 . Пополняя плоскость комплексного переменного так введенной бесконечно удалённой точкой z = , получаем расширенную плоскость комплексного переменного. . Пополняя плоскость комплексного переменного так введенной бесконечно удалённой точкой z = , получаем расширенную плоскость комплексного переменного.1.2. Окрестностью точки z0 плоскости комплексной переменной z называется всякая область, содержащая эту точку. -окрестностью точки zo называется множество всех точек z, лежащих внутри круга радиуса с центром в точке z0, т. е. множество всех точек z, удовлетворяющих неравенству 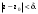 Пусть функция = f (z) определена в некоторой окрестности точки z0, кроме, быть может, самой точки z0. Число А называется пределом функции f ( z) в точке z0, если для любого числа > 0 можно указать такое число > 0, что для всех точек z , удовлетворяющих условию 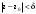 , выполняется неравенство , выполняется неравенство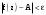 . В этом случае пишут . В этом случае пишут 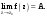 Здесь предполагается, что z0 и А конечные точки комплексной плоскости. Здесь предполагается, что z0 и А конечные точки комплексной плоскости.Определение предела функции f(z) в точке z0 может быть дано и по-другому. Если для любой последовательности 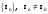 , сходящейся к точке z0 , соответствующая ей последовательность значений функции , сходящейся к точке z0 , соответствующая ей последовательность значений функции 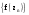 сходится к комплексному числу А, то число А называют пределом функции f (z) в точке z0: сходится к комплексному числу А, то число А называют пределом функции f (z) в точке z0: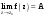 . Здесь конечность z0 и А не предполагается. Существование предела . Здесь конечность z0 и А не предполагается. Существование предела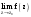 , где , где 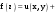 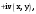 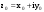 , равносильно существованию двух пределов , равносильно существованию двух пределов 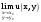 и и 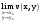 , причём , причём 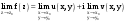 . .Свойства пределов функций комплексного переменного. Пусть существуют пределы 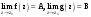 , тогда , тогда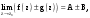 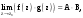 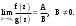 Функция f (z) , заданная в области D, называется непрерывной в точке z0, если 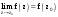 . .Для непрерывности функции  комплексной переменной в точке z0 = x + iy0 необходимо и достаточно, чтобы её действительная и мнимая части, т.е. функции u(x,y) и v(x,y), были непрерывны в точке z0 по совокупности переменных x, y. Функция f(z) комплексного переменного называется непрерывной в области D , если она непрерывна в каждой точке этой области. Сумма, разность, произведение двух функций комплексного переменного f(z) и g(z) , непрерывных в области D , также являются функциями непрерывными в этой области, а функция комплексной переменной в точке z0 = x + iy0 необходимо и достаточно, чтобы её действительная и мнимая части, т.е. функции u(x,y) и v(x,y), были непрерывны в точке z0 по совокупности переменных x, y. Функция f(z) комплексного переменного называется непрерывной в области D , если она непрерывна в каждой точке этой области. Сумма, разность, произведение двух функций комплексного переменного f(z) и g(z) , непрерывных в области D , также являются функциями непрерывными в этой области, а функция  непрерывна в тех точках области D , где g(z) 0. непрерывна в тех точках области D , где g(z) 0.Пример. 1.4. Дана линейная функция = f (z) = az + b, где a и b – комплексные постоянные. Доказать, что в точке z0 эта функция непрерывна, т.е.  . .Доказательство. Возьмём произвольное число 0. Так как  , ,то, выбрав в качестве 0 число 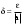 , будем иметь , будем иметь 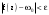 при |z – z0| < . Это означает, что 0 = az0 + b есть предел функции f(z) = az + b в точке z0. при |z – z0| < . Это означает, что 0 = az0 + b есть предел функции f(z) = az + b в точке z0. Поскольку 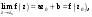 то тем самым доказано, что в любой точке z0 линейная функция непрерывна. то тем самым доказано, что в любой точке z0 линейная функция непрерывна.2.2 Дифференцирование функции комплексного переменного. Условия Коши-Римана. Пусть функция = f(z) определена в некоторой области D комплексного переменного z. Пусть точки z и z + z принадлежат этой области. Обозначим = f(z + z) –f(z), z = x+ iy. Функция = f(z) называется дифференцируемой в точке z D , если отношение z имеет конечный предел при z0 произвольным образом. Этот предел называется производной функции f(z) в точке z и обозначается 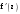 (или (или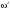 , или , или 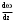 ). Так что по определению ). Так что по определению  . .Если z = x + iy, f(z) = u(x, y) + i v(x, y), то в каждой точке дифференцируемости функции f(z) выполняются соотношения 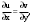 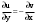 , называемыми условиями Коши-Римана. Верно и обратное. Если в некоторой точке (x, y) функции u(x, y) и v(x, y) дифференцируемы как функции действительных переменных x и y и удовлетворяют условиям , называемыми условиями Коши-Римана. Верно и обратное. Если в некоторой точке (x, y) функции u(x, y) и v(x, y) дифференцируемы как функции действительных переменных x и y и удовлетворяют условиям 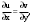 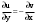 , то функция f(z) = u + iv дифференцируема в точке z = x + iy как функция комплексного переменного z. , то функция f(z) = u + iv дифференцируема в точке z = x + iy как функция комплексного переменного z.Функция = f(z) называется аналитической в данной точке z D, если она дифференцируема как в самой точке, так и в некоторой её окрестности. Функция f(z) называется аналитической в области D, если она дифференцируема в каждой точке этой области. Для любой аналитической функции f(z) имеем 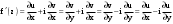 . .Примеры. 2.1. Показать, что функция = еz является аналитической на всей комплексной плоскости. Решение. ez = ex(cos y + i sin y), u(x, y) = excos y, v(x, y) = exsin y. Функции u(x, y) и v(x, y) как функции действительных переменных x и y дифференцируемы в любой точке (x,y) и при этом удовлетворяют условиям Коши-Римана: 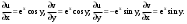 Следовательно, функция = ez всюду аналитическая и 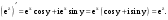 2.2. Является ли функция = z  аналитической хотя бы в одной точке? аналитической хотя бы в одной точке?Решение. Имеем 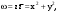 так что u(x,y) = x2 + y2, v(x, y) = 0. Условия Коши-Римана в этом случае имеют вид: так что u(x,y) = x2 + y2, v(x, y) = 0. Условия Коши-Римана в этом случае имеют вид: 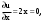 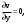   , и выполняются только в одной точке (0, 0). Следовательно, функция , и выполняются только в одной точке (0, 0). Следовательно, функция  дифференцируема только в точке z = 0 и нигде не аналитична. дифференцируема только в точке z = 0 и нигде не аналитична.Покажем, пользуясь определением, что функция  дифференцируема в точке z = 0. Имеем f(0) = 0, поэтому дифференцируема в точке z = 0. Имеем f(0) = 0, поэтому 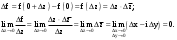  Таким образом, 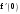 существует и равна 0. существует и равна 0.2.3. Является ли функция 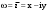 аналитической? аналитической? Решение. u(x, y) = x, v(x, y) = – y – всюду дифференцируемые функции переменных x и y. Далее, 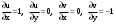 . Так что . Так что 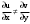 , т. е. первое из условий Коши-Римана не выполняется ни в одной точке комплексной плоскости. Значит функция , т. е. первое из условий Коши-Римана не выполняется ни в одной точке комплексной плоскости. Значит функция 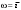 нигде не дифференцируемая, а, следовательно, и не аналитическая. нигде не дифференцируемая, а, следовательно, и не аналитическая.Пользуясь условиями Коши-Римана, аналитическую функцию f(z) можно восстановить, если известна её действительная часть u(x, y) или мнимая часть v(x, y). Пример. 2.4. Найти аналитическую функцию = f(z) по известной действительной части u(x, y) = 2 ex cos y и при дополнительном условии f(0) = 2. Решение. Имеем 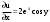 . По первому условию Коши-Римана должно быть . По первому условию Коши-Римана должно быть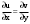 , так что , так что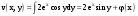 , где (x) пока неизвестна. , где (x) пока неизвестна.По второму условию Коши-Римана 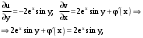 откуда 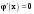 , а значит (x) = C, где C = const. Итак, v(x, y) = 2excos y + C и, следовательно, f(z) = 2excos y + 2exsin y + C = 2ez + C. Из дополнительного условия найдём С: 2 = 2e0 + C. Отсюда, С = 0 и f(z) = 2ez. , а значит (x) = C, где C = const. Итак, v(x, y) = 2excos y + C и, следовательно, f(z) = 2excos y + 2exsin y + C = 2ez + C. Из дополнительного условия найдём С: 2 = 2e0 + C. Отсюда, С = 0 и f(z) = 2ez.Аналитическую в окрестности точки z0 функцию f(z) можно восстановить также по одной из следующих формул: 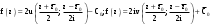 , ,где 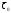 – сопряжённое число для C0 = f(z0), а – сопряжённое число для C0 = f(z0), а 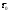 – сопряжённое число для z0. – сопряжённое число для z0.Пример. 2.5. Найти аналитическую функцию = f(z) по известной мнимой части v(x,y) = 3x + 2xy при условии f(– i) = 2. Решение. В нашем примере z0 = – i, C0 = 2, следовательно, 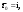 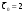 , так что , так что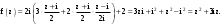 Функция (x, y) называется гармонической в области D, если она имеет в этой области непрерывные частные производные до второго порядка включительно и удовлетворяет в этой области уравнению Лапласа 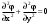 . .Если функция f(z) = u + iv аналитична в некоторой области, то её действительная часть u(x,y) и мнимая часть v(x, y) являются в этой области гармоническими функциями. Однако, если u1(x, y) и v1(x, y) любые две гармонические функции, то функция f1(z) = u1 + iv1 не обязательно будет аналитической функцией: для аналитичности f1(z) нужно, чтобы функции u1 и v1 удовлетворяли условиям Коши-Римана. Две гармонические функции, удовлетворяющие условиям Коши-Римана, называются сопряжённой парой гармонических функций (порядок функций в паре существенен). Пример. 2.6. Найти все гармонические функции вида u = f(x2 + y2), отличные от постоянной. Решение. Так как искомые функции гармонические, то они должны удовлетворять уравнению Лапласа 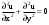 . Пусть t = x2 + y2, тогда u = f(t), где t = t(x, y). По правилу дифференцирования сложной функции находим: . Пусть t = x2 + y2, тогда u = f(t), где t = t(x, y). По правилу дифференцирования сложной функции находим: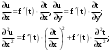 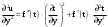 . .Складывая последние два равенства, получим 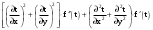 . .Так как 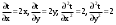 , , то 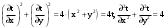 . .Имеем 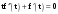 или или 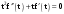 – получили уравнение Эйлера. – получили уравнение Эйлера.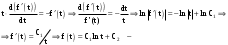 общее решение этого уравнения, где С1 и C2 – const. Итак, искомые гармонические функции имеют вид u = f(x2+ y2) = C1ln(x2 + y2) + C2. Геометрический смысл модуля и аргумента производной. Пусть функция f(z) аналитическая в точке z0 и 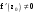 . Тогда . Тогда 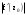 равен коэффициенту растяжения в точке z0 при отображении = f(z) плоскости z на плоскость ; точнее, при равен коэффициенту растяжения в точке z0 при отображении = f(z) плоскости z на плоскость ; точнее, при 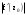 > 1 имеет место растяжение, а при > 1 имеет место растяжение, а при 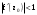 – сжатие. – сжатие.Аргумент производной 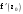 геометрически равен углу, на который нужно повернуть касательную в точке z0 к любой гладкой кривой на плоскости z, проходящей через точку z0, чтобы получить направление касательной в точке 0 = f(z0) к образу этой кривой на плоскости при отображении = f(z). При этом, если геометрически равен углу, на который нужно повернуть касательную в точке z0 к любой гладкой кривой на плоскости z, проходящей через точку z0, чтобы получить направление касательной в точке 0 = f(z0) к образу этой кривой на плоскости при отображении = f(z). При этом, если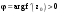 , то поворот происходит против часовой стрелки, а при < 0 – по часовой. , то поворот происходит против часовой стрелки, а при < 0 – по часовой.Пример. 2.7. Найти коэффициент растяжения и угол поворота при отображении = z2 в точке 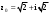 . .Решение. Имеем 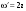 . Так что . Так что 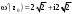 или в тригонометрической форме или в тригонометрической форме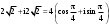 . Значит, . Значит, 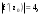 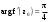 , т. е. коэффициент растяжения r = 4, а угол поворота , т. е. коэффициент растяжения r = 4, а угол поворота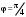 . .Если функция = f(z), аналитическая в некоторой области D, взаимно однозначно отображает эту область на область 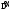 , то кривая L, лежащая в области D, отобразится в некоторую кривую , то кривая L, лежащая в области D, отобразится в некоторую кривую 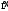 в области в области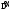 , длина которой равна , длина которой равна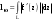 , а площадь области , а площадь области  выражается формулой выражается формулой . Таким образом, . Таким образом,  равен коэффициенту искажения площади при отображении = f(z). равен коэффициенту искажения площади при отображении = f(z).Пример. 2.8. Точка z = x + iy описывает отрезок x = 1, –1 y 1. Чему равна длина линии, получающейся при отображении этого отрезка с помощью функции = z2 ? Решение. Первый способ. Имеем = z2 или x2 – y2 + i 2xy, т. е. u = x2 – y2, v = 2xy. На линии x = 1, –1 y 1 будем иметь u= 1 – y2, v = 2y, причём –2 v 2. Так как  , то , то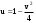 . Длина дуги параболы . Длина дуги параболы 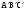  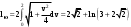 . .Второй способ. 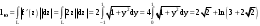 . .ЗАКЛЮЧЕНИЕ Аналитическая функция это обширная тема математики, которая часто используется в различных сферах. В данной курсовой работе мы рассмотрели некоторые вопросы относящиеся к данной теме. В частности рассмотрены следующие вопросы: Понятие числовой последовательности Понятие предела последовательности А также рассмотрены некоторые частные случаи данных последовательности. Решены несколько примеров а также подробно решено и объяснено решение сложной задачи. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Зорич, В.А (1997) Математический анализ, т. 1 и 2, Фазис : Москва. |
