лекции теор. мех (копия). Предмет теоретической механики изучение механического движения и механического взаимодействия материальных тел
 Скачать 0.97 Mb. Скачать 0.97 Mb.
|
|
Основная задача статики. Содержание статики абсолютно твердого тела составляют две основные задачи: 1. Задача о приведении системы сил: как данную систему сил заменить другой, в частности наиболее простой, ей эквивалентной? 2. Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу (или материальной точке), чтобы она была уравновешенной системой? Первая основная задача имеет важное значение не только в статике, но и в динамике. Вторая задача часто ставится в тех случаях, когда равновесие заведомо имеет место, например, когда заранее известно, что тело находится в равновесии, которое обеспечивается связями, наложенными на тело. При этом условия равновесия устанавливают зависимость между всеми силами, приложенными к телу; во многих случаях с помощью этих условий удается определить опорные реакции. Хотя этим не ограничивается сфера интересов статики твердого тела, но нужно иметь в виду, что определение реакций связей (внешних и внутренних) необходимо для последующего расчета прочности конструкции. В более общем случае, когда рассматривается система тел, имеющих возможность перемещаться друг относительно друга, одной из основных задач статики является задача определения возможных положений равновесия. Эти вопросы рассматриваются в аналитической статике. Решение задач на равновесие твердого тела, независимо от взаимного расположения приложенных к телу сил, рекомендуется проводить в следующем порядке: 1) выделить твердое тело, равновесие которого надо рассмотреть для отыскания неизвестных величин; 2) изобразить активные силы; 3) если твердое тело несвободно, то, примени» закон освобождаемости от связей, приложить к нему соответствующие реакции связей; 4) рассмотреть равновесие данного несвободного твердого тела, как тела свободного, находящегося под действием активных сил и реакций связей; 5) использовать необходимые и достаточные условия (уравнения) равновесия в соответствии со взаимным расположением сил, приложенных к твердому телу, и определить искомые величины. 1. Сходящиеся силы. Геометрический и аналитический способы сложения сил. Равнодействующая сходящихся сил. Сходящиеся силы — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке (рис. 3.1, а).  Рисунок 3.1. Система сходящихся сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем в дальнейшем называть главным вектором этой системы сил. 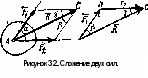 Сложение двух сил. Геометрическая сумма 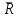 двух сил двух сил 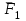 и и 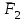 находится по правилу параллелограмма (рис. 3.2, а) или построением силового треугольника (рис. 3.2, б),изображающего одну из половин этого параллелограмма. Если угол между силами равен , то модуль Rи углы , , которые сила находится по правилу параллелограмма (рис. 3.2, а) или построением силового треугольника (рис. 3.2, б),изображающего одну из половин этого параллелограмма. Если угол между силами равен , то модуль Rи углы , , которые сила 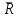 образует со слагаемыми силами, определяются по формулам: образует со слагаемыми силами, определяются по формулам: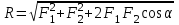 (3.1) (3.1)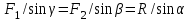 (3.2) (3.2)2. Сложение системы сил. Геометрическая сумма любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника (рис. 3.1, б). Соединяя начало первого вектора с концом последнего, получаем вектор 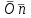 , изображающий геометрическую сумму или главный вектор слагаемых сил: , изображающий геометрическую сумму или главный вектор слагаемых сил: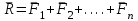 или или  . (3.3) . (3.3)3. Равнодействующая сходящихся сил. Рассмотрим систему сходящихся сил, т. е. сил, линии действия которых пересекаются в одной точке (рис. 3.3, а). 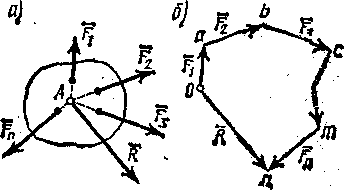 Рисунок 3.3. Равнодействующая сходящихся сил. Система сходящихся сил имеет равнодействующею, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия (рис. 3.2, б). Задача 1. Кронштейн состоит из стержней АС и ВС, соединенных со стеной и друг с другом шарнирами, причем 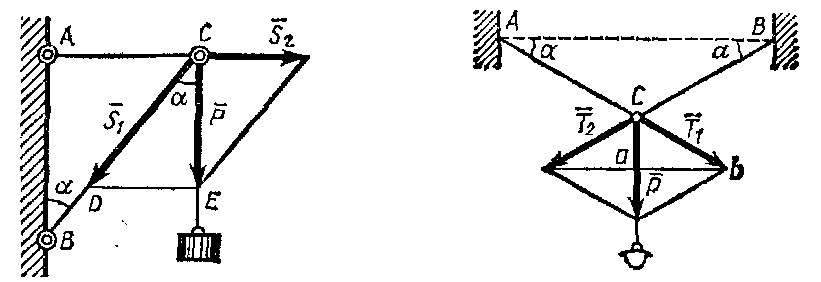 Рисунок 3.4 Кронштейн Рисунок 3.5. Фонарь подвешенный на двух тросах Решение. Под усилиями в стержнях понимают значения сил, растягивающих или сжимающих эти стержни. Так как стержни считаются невесомыми, то их реакции (они действуют на шарнир С) направлены вдоль стержней. Тогда для определения искомых усилий приложим силу в точке С и разложим ее по направлениям АС и СВ. Составляющие и и будут искомыми силами. Из треугольника CDE находим: Таким образом, стержень ВС сжимается силой а стержень АС растягивается силой . С увеличением угла а усилия в стержнях растут и при а, близком к 90°, могут достигать очень больших размеров. Задача 2. Фонарь весом Р=200 Н (рис. 3.5) подвешен на двух тросах АС и ВС, образующих с горизонтальной прямой одинаковые углы а=5°. Определить, с какой силой натянуты тросы. Решение. Приложим силу Р в точке С и разложим ее по направлениям тросов. Параллелограмм сил в данном случае будет ромбом; диагонали его взаимно перпендикулярны и делятся в точке пересечения пополам. Из треугольника находим, что Из полученной формулы видно, что с уменьшением угла а натяжение тросов значительно увеличивается (например, при 4. Проекция силы на ось и на плоскость. Проекция силы на ось есть алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси. Так, для сил, изображенных на рис. 3.6, 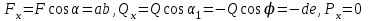 (3.4) (3.4)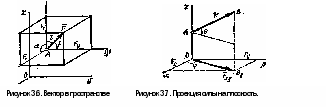 Проекцией силы Проекцией силы 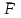 на плоскость Oxy называется вектор на плоскость Oxy называется вектор 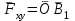 , заключенный между проекциями начала и конца силы , заключенный между проекциями начала и конца силы 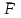 на эту плоскость (рис. 3.7). Проекция силы на плоскость есть величина векторная. По модулю на эту плоскость (рис. 3.7). Проекция силы на плоскость есть величина векторная. По модулю 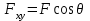 , где , где 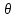 — угол между направлением силы — угол между направлением силы 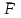 и ее проекции и ее проекции 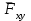 . .5. Аналитический способ задания сил. Для аналитического задания силы необходимо выбрать систему координатных осей Охуz, по отношению к которой будет определяться направление силы в пространстве. 6. Аналитический способ сложения сил. Теоремы геометрии: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Согласно этой теореме, если  есть сумма сил есть сумма сил  , ,  , , ,. . . , ,. . . ,  , т.е. , т.е. (3.5) (3.5)Зная Rх, Rу и Rz, по формулам (5) находим:  (3.6) (3.6)Векторное и аналитические условия равновесия сходящихся сил. Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая, а следовательно, и главный вектор этих сил были равны нулю. 1. Геометрическое условие равновесия. Главный вектор R системы сил может обратиться в нуль только тогда, когда конец последней силы в многоугольнике совпадает с началом первой силы, т. е. когда многоугольник замкнется. 2. Аналитические условия равновесия. Аналитически модуль главного вектора системы сил определяется формулой  (3.7) (3.7)Так как под корнем стоит сумма положительных слагаемых, то  обратится в нуль только тогда, когда одновременно Rx=0, Ry=0, Rz=0, т. е. обратится в нуль только тогда, когда одновременно Rx=0, Ry=0, Rz=0, т. е.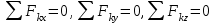 . (3.8) . (3.8)Равенства (3.8) выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю. Очевидно, что условия равновесия (как в аналитической, так и в геометрической форме) позволяют проконтролировать, находится ли в равновесии заданная система сил. Однако еще большее практическое значение имеет другая возможность использования этих условий. Часто заведомо известно, что вследствие наложенных связей тело находится в равновесии, причем мы знаем только часть действующих сил, а именно, активные силы; при этом опорные реакции известны лишь отчасти (например, известны их направления). Тогда с помощью условий равновесия можно найти остальные неизвестные, определяющие реакции связей. Условия равновесия, в которые входят неизвестные, будут уже служить уравнениями для определения этих неизвестных. Конечно, определение неизвестных возможно лишь в тех случаях, когда число неизвестных составляющих реакций не больше числа уравнений равновесия. Для определенности решения пространственной задачи на равновесие системы сходящихся сил она должна содержать не более трех неизвестных (соответственно трем уравнениям равновесия), а для плоской задачи — не более двух. Если неизвестных реакций больше, чем уравнений равновесия, в которые эти реакции входят, то задача не может быть решена только методами статики твердого тела (статически неопределимая задача)2. Хотя выбор направления координатных осей, на которые проектируются силы, не имеет принципиального значения, однако при решении задач для получения более простых уравнений равновесия рационально иногда направлять координатные оси перпендикулярно неизвестным силам; при этом некоторые уравнения равновесия будут содержать меньшее число неизвестных, чем их содержится в задаче. 3. Теорема о трех силах. (Теорема о трех непараллельных силах) При решении задач статики иногда удобно пользоваться следующей теоремой: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке. 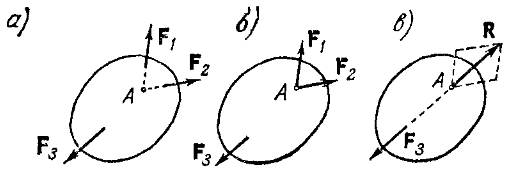 Рисунок 3.8. Теорема о трех непараллельных силах Задача 3. Найти сумму трех лежащих в одной плоскости сил (рис. 3.9, а), если дано: Решение. Вычисляем проекции заданных сил на координатные оси} FX=F cos Тогда по формулам (6) Следовательно, Окончательно Для решения той же задачи геометрическим методом надо, выбрав соответствующий масштаб (например, в 1 см — 10 Н), построить из сил у 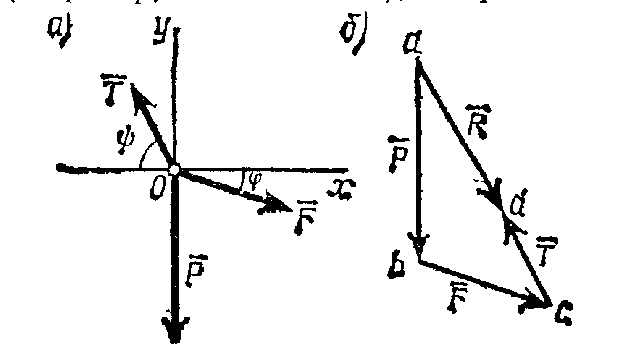 Рис. 3.9. Силовой многоугольник. силовой многоугольник (рис. 3.9, б). Его замыкающая и определяет в данном масштабе модуль и направление Если, например, при измерении получим ad ≈ 2,5 см, то, следовательно, Алгебраический момент силы относительно точки. Момент силы относительно точки как вектор. Момент силы относительно точки О – это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке (рис. 4.1). 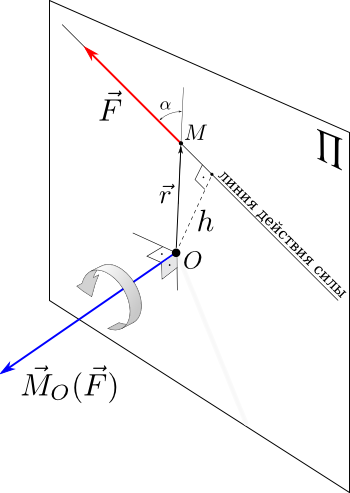 Рисунок 4.1. Момент силы относительно точки О. Если известен радиус-вектор r точки приложения силы F относительно точки О, то момент этой силы относительно О выражается следующим образом: Действительно, модуль этого векторного произведения: |MO|=|r×F|=|r||F|sinα. В соответствии с рисунком |r|sinα=h, поэтому: |MO|=|F|h. Вектор MO, как и результат векторного произведения, перпендикулярен векторам r и F, которые принадлежат плоскости Π. Направление вектора MO таково, что глядя по направлению этого вектора, кратчайшее вращение от r к F происходит по часовой стрелке. Другими словами, вектор MO достраивает систему векторов (r, F) до правой тройки. Зная координаты точки приложения силы в системе координат, начало которой совпадает с точкой О, и проекцию силы на эти оси координат, момент силы может быть определен следующим образом: 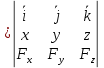 =(y =(y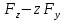 ) )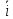 + (z + (z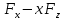 ) ) + (x + (x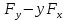 ) )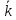 (4.1) (4.1) 2. Момент силы относительно оси; связь между моментами силы относительно оси и относительно точки, лежащей на этой оси. Проекция момента силы относительно точки на некоторую ось, проходящую через эту точку называется моментов силы относительно оси. 2. Момент силы относительно оси; связь между моментами силы относительно оси и относительно точки, лежащей на этой оси. Проекция момента силы относительно точки на некоторую ось, проходящую через эту точку называется моментов силы относительно оси.Момент силы относительно оси вычисляется как момент проекции силы F на плоскость Π, перпендикулярную оси, относительно точки пересечения оси с плоскостью Π: Знак момента определяется направлением вращения, которое стремится придать телу сила F→Π. Если, глядя по направлению оси Oz сила вращает тело по часовой стрелке, то момент берется со знаком ``плюс'', иначе - ``минус''. Рассмотрим проекции вектора 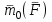 на разные оси. Проекция вектора на разные оси. Проекция вектора 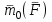 , т. е. момента силы , т. е. момента силы 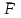 относительно центра О, на какую-нибудь ось z, проходящую через этот центр, называется моментом силы относительно центра О, на какую-нибудь ось z, проходящую через этот центр, называется моментом силы 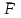 относительно оси z, т. е. относительно оси z, т. е.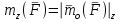 или или 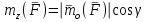 , (4.2) , (4.2) где  — момент силы — момент силы  относительно оси z; —угол между вектором относительно оси z; —угол между вектором  и осью z. Из определения следует, что mz(F), как проекция вектора на ось, является величиной алгебраической (знак тг(р) определяется так же, как знак проекции любого вектора. и осью z. Из определения следует, что mz(F), как проекция вектора на ось, является величиной алгебраической (знак тг(р) определяется так же, как знак проекции любого вектора. или или  . (4.3) . (4.3)Таким образом, момент силы  относительно оси z равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси z, взятому относительно точки O пересечения оси с этой плоскостью. относительно оси z равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси z, взятому относительно точки O пересечения оси с этой плоскостью.Точку, относительно которой берется момент, называют центром момента, а момент силы относительно этой точки – моментом относительно центра. Моментом силы  относительно центра О называется приложенный в центре О вектор относительно центра О называется приложенный в центре О вектор  , модуль которого равен произведению модуля F силы, на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки. Согласно этому определению , модуль которого равен произведению модуля F силы, на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки. Согласно этому определению (4.4) (4.4)Последний результат следует из того, что  . Измеряется момент силы в ньютон-метрах (Нм). . Измеряется момент силы в ньютон-метрах (Нм).3. Аналитические формулы для моментов силы относительно осей координат. 4. Теорема Вариньона о моменте равнодействующей. Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра О равен сумме моментов сил системы относительно того же центра. 5. Пара сил. Момент пары как вектор. Эквивалентность пар. Сложение пар сил. Условие равновесия системы пар. Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.  Рисунок 4.3. Пара сил Плоскость, проходящая через линии действия пары сил, называется плоскостью действия пары. Расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело характеризуется величиной, называемой моментом пары. Моментом пары сил называется вектор  (или (или 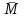 ), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. ), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.Эквивалентность пар: действие пары сил на твердое тело не изменится, если переместить пару в другое положение в плоскости ее действия; плоскость ее действия переместить параллельно самой себе; любым образом изменить модули сил и плечо пары, сохранив неизменным их произведение, т.е. момент пары M=F · d. Теорема о сложении пар: система пар, действующих на абсолютно твердое тело, эквивалентнаодной паре с моментом, равным геометрической сумме моментов слагаемых пар т.е. . (4.5)  Докажем эту теорему сначала для двух пар. Докажем эту теорему сначала для двух пар. Пусть на тело в плоскости 1 действует пара (F '1, F '2), а в плоскости 2 пара (P '1, P '2) (рис.4.4). На линии пересечения плоскостей выберем отрезок АВ и приведем пары к одному плечу. Получим пары (F1, F2) и (P1, P2), моменты которых M1 и M2. Отложим векторные моменты от точки В. Сложим силы в точках А и В по правилу параллелограмма. Получим пару сил (R*1, R*2), причем: . Найдем векторный момент полученной пары, используя формулу (10), Таким образом, векторный момент M изображается диагональю параллелограмма, построенного на векторных моментах M1 и M2. Пусть теперь дано n пар, как угодно расположенных в пространстве. Складывая последовательно все пары сил изложенным выше способом, получим эквивалентную пару, векторный момент которой равен геометрической сумме векторных моментов заданных пар сил т.е.: что и требовалось доказать. Момент эквивалентной пары сил изображается замыкающей стороной многоугольника, построенного в произвольной точке, причем стороны этого многоугольника геометрически равны моментам слагаемых пар (рис.4.3). Если пары лежат в параллельных плоскостях, то на основании доказанной в теоремы их можно перенести в одну плоскость. Моменты этих пар будут направлены по перпендикуляру к этой плоскости в ту или иную сторону в зависимости от направления вращения пар в плоскости. Так как моменты пар будут направлены по одной прямой, то момент эквивалентной пары будет равен алгебраической сумме моментов слагаемых пар, т.е.: . (4.6) Условие равновесия системы пар, приложенных к твердому телу: M = Mk=0. 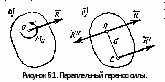 1. Теорема о параллельном переносе силы (Основная лемма (теорема) статики). 1. Теорема о параллельном переносе силы (Основная лемма (теорема) статики). Плоская система сил тоже приводится к силе, равной 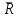 и приложенной в произвольно выбранном центре О, и паре с моментом Мо, но сила и пара лежат в данном случае в одной плоскости – в плоскости действия сил (рис. 4.1, а), где пара изображена дуговой стрелкой). и приложенной в произвольно выбранном центре О, и паре с моментом Мо, но сила и пара лежат в данном случае в одной плоскости – в плоскости действия сил (рис. 4.1, а), где пара изображена дуговой стрелкой). Таким образом, для плоской системы сил 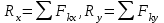 , ,  (5.1) (5.1)2. Приведение произвольной системы сил к данному центру. Главный вектор и главный момент системы сил. Пусть на твердое тело действует произвольная система сил  , ,  , , ,. . . , ,. . . ,  . Выберем какую-нибудь точку О за центр приведения и, пользуясь теоремой, перенесем все силы в центр О, присоединяя при этом соответствующие пары. Тогда на тело будет действовать система сил . Выберем какую-нибудь точку О за центр приведения и, пользуясь теоремой, перенесем все силы в центр О, присоединяя при этом соответствующие пары. Тогда на тело будет действовать система сил , ,  ,. . . , ,. . . ,  , (5.2) , (5.2)приложенных в центре О, и система пар, моменты которых согласно равны:  , ,  ,…….., ,……..,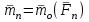 (5.3) (5.3)Сходящиеся силы, приложенные в точке О, заменяются одной силой 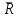 , приложенной в точке О. При этом , приложенной в точке О. При этом 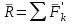 или, или,  Как известно, величина 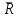 , равная геометрической сумме всех сил, называется главным вектором системы сил; величина , равная геометрической сумме всех сил, называется главным вектором системы сил; величина 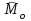 , равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы сил относительно этого центра. , равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы сил относительно этого центра.Теорема о приведении системы сил: Любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой 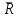 , равной главному вектору системы сил приложенной в центре приведения О, и одной парой с моментом , равной главному вектору системы сил приложенной в центре приведения О, и одной парой с моментом 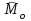 , равным главному моменту системы сил относительно центра О. , равным главному моменту системы сил относительно центра О.Пусть на твердое тело действует система сил (F1,F2, ... Fn). Приведем эту произвольную систему сил к центру О (рис. 5.2,а). Каждую силу будем приводить рассмотренным выше способом. После приведения в центре получим силы F '1, F '2, ... F 'n, геометрически равные данным силам: , (5.4) и пары сил (F "1, F1), (F "2, F2),...(F "n, Fn) с моментами, равными моментам сил относительно центра приведения: Силы F'1, F'2, ... F'n заменим результирующей силой, равной геометрической сумме этих сил: . Учитывая равенства (13.1), можно записать: (5.6) Сила R называется главным вектором системы сил. 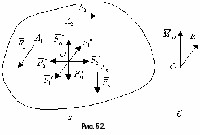 Таким образом, главным вектором системы сил называется геометрическая сумма всех сил системы. Главный вектор представляет собой замыкающую сторону силового многоугольника, построенного в любой точке пространства на силах системы, т.е. главный вектор не зависит от центра приведения. Главный вектор не является равнодействующей, так как он в общем случае не эквивалентен первоначальной системе сил. Таким образом, главным вектором системы сил называется геометрическая сумма всех сил системы. Главный вектор представляет собой замыкающую сторону силового многоугольника, построенного в любой точке пространства на силах системы, т.е. главный вектор не зависит от центра приведения. Главный вектор не является равнодействующей, так как он в общем случае не эквивалентен первоначальной системе сил. Систему из n присоединенных пар с моментами M1, M2 ,..., Mn можно, используя теорему о сложении пар сил, заменить одной парой с моментом, равным геометрической сумме моментов присоединенных пар: . Учитывая равенства (10), можно записать: M0, называют главным моментом системы сил относительно центра О. Таким образом, главным моментом системы сил относительно центра называется геометрическая сумма векторных моментов всех сил системы относительно этого центра. Главный момент системы сил зависит от положения центра приведения в пространстве. Итак, после приведения произвольной системы сил в центре приведения получаем силу, равную главному вектору, и пару сил, момент которой равен главному моменту системы сил относительно центра приведения (рис.5.2, б). В этом заключается основная теорема статики абсолютно твердого тела. Для сил, расположенных в одной плоскости, главный момент относительно центра приведения равен сумме алгебраических моментов всех сил системы относительно этого центра: . (5.8) Векторы M0, R обычно определяют аналитически. Для этого через центр О проведем оси прямоугольных координат и найдем проекции этих векторов на оси. Проецируя векторное равенство (5.6) на оси координат, найдем проекции главного вектора R: . Модуль главного вектора определится по формуле: , (5.9) а направление – с помощью направляющих косинусов: Проецируя векторное равенство (4.8) на оси координат, учитывая при этом, что проекция векторного момента силы на ось равна моменту силы относительно этой оси, получим: где главные моменты системы относительно координатных осей. Модуль главного момента относительно центра О, начала координат, определится по формуле: , (4.10) а направление – с помощью направляющих косинусов: Для плоской системы сил, расположенной в плоскости xOy получаем: , Случаи, когда главный вектор или главный момент равен нулю. Для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю, т. е. чтобы выполнялись условия 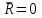 , , 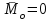 (6.1) (6.1) где О – любой центр. Условия равновесия произвольной плоской и пространственной систем сил. Равновесие плоской системы сил. Необходимые и достаточные условия равновесия любой системы сил даются равенствами 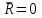 и и 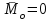 . . Основная форма условий равновесия. Так как вектор 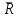 равен нулю, когда равны нулю его проекции Rх и Rу, то для равновесия должны выполняться равенства Rх =0, Rу =0 и М0 =0, где в данном случае Мо — алгебраический момент, а О — любая точка в плоскости действия сил. Тогда равен нулю, когда равны нулю его проекции Rх и Rу, то для равновесия должны выполняться равенства Rх =0, Rу =0 и М0 =0, где в данном случае Мо — алгебраический момент, а О — любая точка в плоскости действия сил. Тогда , (6.2) , (6.2)Формулы (25) выражают следующие аналитические условия равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю. Вторая форма условий равновесия: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких – нибудь двух центров А и В и сумма их проекций на ось Ох; не перпендикулярную прямой АВ, были равны нулю:  (6.3) (6.3)Третья форма условий равновесия (уравнения трех моментов): для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В и С, не лежащих на одной прямой, были равны нулю:  . (6.4) . (6.4)Равновесие плоской системы параллельных сил. В случае, когда все действующие на тело силы параллельны друг другу, можно направить ось Ох перпендикулярно силам, а ось Оу параллельно им. В результате для параллельных сил останется два условия равновесия:  (6.5) (6.5)где ось Оу параллельна силам. Условия равновесия произвольной пространственной системы сил запишутся так: Так как при равновесии модули этих векторов должны равняться 0, то отсюда вытекает шесть уравнений равновесия произвольной пространственной системы сил:   Для равновесия произвольной системы сил в пространстве необходимо, чтобы сумма проекций всех сил на каждую из трех координатных осей и сумма моментов всех сил относительно каждой из трех координатных осей равнялись нулю. Для равновесия произвольной системы сил в пространстве необходимо, чтобы сумма проекций всех сил на каждую из трех координатных осей и сумма моментов всех сил относительно каждой из трех координатных осей равнялись нулю.3. Случай параллельных сил. Рассмотрим равновесие пространственной системы параллельных сил как частный случай равновесия произвольной системы сил. Выберем оси координат так, чтобы ось Оz была параллельна линиям действия Ξ сил (рис.6.1) Так как проекции сил на оси x и y, а также моменты сил относительно оси z равны нулю, то в формулах (1.64) уравнения 1, 2, 6 обращаются в тождества 0Ξ 0 и вместо шести уравнений равновесия получаем три уравнения: |
